as the lower block carrying the weight, and in the absence of friction and other resistances the mechanical advantage will be in the same ratio of the effort to the resistance. In practice the full advantage of this or any other similar combination is not realized, because of the friction of the sheaves against the pin or shaft, and more important still is the stiffness of the rope, which requires work to be done upon it to bend it round the sheave and straighten it again. The effect of pin friction is equivalent - to diminishing the radius of the effort and A increasing that of the resistance, For a single pulley of diameter D, turning on a fixed pin of diameter d, the relation of the effort E to the load W, where f is the coefficient of friction, is expressed by E/W = (D -l-fd)/(D -jd) = 12" I-lf-2fd/D approximately. The resistance of the rope to bending causes an additional resistance, which experiment shows can be expressed in°the form Wd"/cD where c is a coefficient. Hence E =W(1+2fd/D+d2/CD) = kW for a single pulley. In a six-sheaved pulley tackle the relation between E and W may be expressed as W = E (I/k+I/kz-l-I/k3+I/k'+I/kf-l-I/k") = E(k° - I)/k"(k-1), and with a probable value of k=-1-I this gives W =4'355 E instead of W=6E. If the free end of the rope is released the weight will descend, and the tackle is then said to overhaul. The conditions which enable a pulley tackle to sustain a weight when the effort is removed may be examined, to a first approximation, if we assume that the internal friction acts in such a way as virtually to diminish the effort E and to increase the resistance R by - amounts proportional to the magnitude of each, and in addition to cause a loss M due to the weights of the parts themselves. lVe may therefore express the relation 'in the form (L-a)E=(1+b)R-l-M, whence we obtain R/E=(I -a)/(I+ b-l-M/R). If now the machine be reversed and R becomes an effort corresponding to a resistance E' then we have R(1-b)= (1 +a)E'+M, giving E'/R=(i-b-M/Rl/(I+f1l (I) If the load is self-sustaining E' is zero or negative, and hence 1;-}-M/R must be equal to or greater than unity, and therefore it is impossible for the ratio of R/E to rise to a greater value than (I -0)/2, and hence at least half the effort is wasted if the tackle

Fig. 5.—Sheave Pulley Block.

Fig. 6.—Weston Differential Pulley Block.

Fig. 7.—Moore and Head Pulley Block.
has the valuable property of sustaining a load when the effort is removed. If, however, an artificial resistance can be introduced, to come into action only when the effort is removed, it is possible to obtain a, tackle of greater efficiency. As an example we may take the case where a brake is provided offering a resistance, c R, proportional to the load sustained, and where the values a and b are small compared with unity. Equation (I) becomes E/R= (I-b-c-lfl/R)/(I -a), and hence b+c-i-M/R is equal to 643 or greater than unity when the load is self-sustained, and we thus obtain a relation between R and E in the form I -a/2 -c, which shows to a first approximation, that as c approaches unity a high efficiency is obtainable, while the self-sustaining power of the tackle is retained. In order to obtain a greater ratio of R to E, without using a large number cl sheaves, various arrangements are used, of which the Weston differential pulley block is a typical example. The upper block carries a pair of chain pulleys A (fig. 6), secured together and of slightly different effective diameters D and d. An endless chain B, passing through guides C and D, encircles these pulleys and the single loose pulley E of the lower block, as indicated. With this arrangement a single revolution of the upper sheave causes the endless chain to wind up the chain on one side by an amount 1rD, and to unwind an amount 1rd on the other side, and in consequence the lower sheave is raised by 1r(D-d)/2. Hence, neglecting friction, E11-D=%R1r(D-d), i.e. E=%R(I -d/D). The value d/D usually lies between the limits I0/II and 15/16, and, if a greater difference of E from R is required, a further mechanical advantage can be obtained by employing a separate hand-wheel and chain, or by forming the upper sheave with an annular spur wheel gearing with a pinion driven by a hand-wheel and chain, as in the Tangye form of Weston pulley-block. The efficiency of the Weston pulley-block is less than 50 %, and it does not therefore overhaul. An objection to this form of block is the great length of the endless chain, which may drag on the ground and pick up dirt and grit, and thereby interfere with the smooth working of the mechanism. Other forms, which do not require so lengthy a chain, sometimes employ an epicyclic train to obtain the reduced velocity of the load. The Moore and Head block has two equal chain-wheels A, B, fig. 7, loosely mounted on an axle C, and provided with annular toothed gear-wheels which usually differ by one tooth. A spur pinion D, gearing with both wheels, is carried loosely upon an eccentric E forming part of the central pin, so that when this latter is turned by the hand-wheel F and chain G the axis of the pinion describes a circle the diameter of which equals the throw of the eccentric, and a small relative motion of the two sheaves takes place, depending on the number of the teeth of the annular wheels. The motion obtained is divided between the two vertical parts of the chain H, which is wrapped round each sheave in opposite directions, with a free loop I between, while the ends are attached to the lifting hook. This form is self-sustaining at all loads. In order to obtain a-self-sustaining pulley tackle, which will have an efficiency of more than 50 %, various arrangements are adopted, which during lifting automatically throw out of action a brake and cause it to come into action again when the effort is removed. A worm-gear tackle of this description is shown in fig. 8, in which a worm A, operated by a hand-wheel B and chain C, drives the worm-wheel D, thereby coiling up a chain E, one end F of which is secured to the upper block, and the other end hangs loosely, after passing round the sprocket wheel. The worm is of great pitch, so that if the effort were removed the weight would descend, did not the axial end thrust of the worm shaft throw into action a friction brake H, the resistance of which prevents motion downwards. In the brake shown, the cone I is pressed against a corresponding recess in the ratchet wheel ], which latter turns loosely in the casing and is provided with a pawl not shown in the figure; this pawl allows freedom of motion when the load is being raised. The frictional grip between the two surfaces l ? 9 U ¢?4 . fa Q I / ¢ 1 é an, of [nn]/: ka ~»<» -!l»|||un gv »» |(~| /0, F ul ndibu prevents return motion of the worm shaft and the load remains suspended, but it may be lowered by turning the hand-wheel so as to overcome the friction brake. Various other arrangements of friction brakes have been devised to give a resistance proportional to the load. Blocks, for lifting very heavy weights, are sometimes provided with an electric motor for driving the worm. The worm-wheel shaft then sometimes carries a spur-pinion gearing with a spur-wheel on the lifting shaft, whereby a much greater mechanical advantage is obtained with a small loss by friction of the spur gearing. REFERENCES.-W. ]. M. Rankine, Machinery and Millwork and Applied Mechanics; W. C. Unwin, Machine Design; Ad. Ernst, lz I I "Za D I I 'if 2 1 @> % I l' J f H "' 'ffl Ill
4, .= 1; ((~l 5 |' I E Q (..) [Tl 1 (nil ('l I (.a ~ Q V f's|P? A
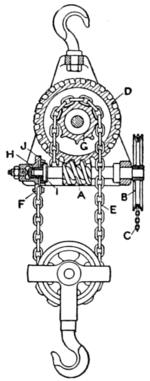
Fig. 8.—Worm-gear Pulley Block with Automatic Brake.
