And if the arc BL be equal to the arc EN, the angle BGL is equal to the angle EHN; [III. 27.
and if the arc BL be greater than the arc EN, the angle BGL is greater than the angle EHN; and if less, less.
Therefore since there are four magnitudes, the two arcs BC,EF, and the two angles BGC, EHF;
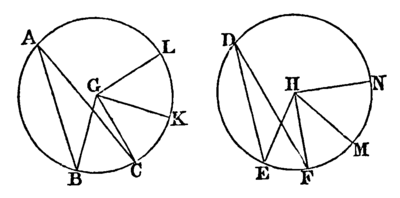 and that of the arc BC and of the angle BGC have been taken any equimultiples whatever, namely, the arc BL and the angle BGL;
and that of the arc BC and of the angle BGC have been taken any equimultiples whatever, namely, the arc BL and the angle BGL;
and of the arc EF and of the angle EHF have been taken any equimultiples whatever, namely, the arc EN and the EHN;
and since it has been shewn that if the arc BL be greater than the arc EN, the angle BGL is greater than the angle EHN; and if equal, equal; and if less, less;
therefore as the arc BC is to the arc EF, so is the angle BGC to the angle EHF. [V. Definition 5.
But as the angle BGC is to the angle EHF, so is the angle BAC to the angle EDF, [V. 15.
for each is double of each; [III. 20.
therefore, as the arc BC is to the arc EF so is the angle BGC to the angle EHF, and the angle BAC to the angle EBF.
Also as the arc BC is to the arc EF, so shall the sector BGC be to the sector EHF.
Join BC, CK, and in the arcs BC, CK take any points X, O, and join BX, XC, CO, OK.
