PROPOSITION 1. PROBLEM.
To describe an equilateral triangle on a given finite straight line.
Let AB be the given straight line; it is required to describe an equilateral triangle on AB.
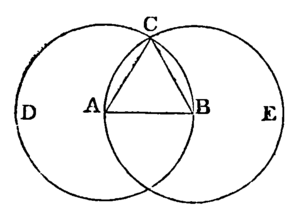
From the centre A at the distance AB describe the circle BCD. [Postulate 3.
From the centre B, at the distance BA, describe the circle ACE. [Postulate 3.
From the point C, at which the circles cut one another, draw the straight lines CA and CB to the points A and B. [Post. 1.
ABC shall be an equilateral triangle.
Because the point A is the centre of the circle BCD, AC is equal to AB. [Definition 15.
And because the point B is the centre of the circle ACE, BC is equal to BA. [Definition 15.
But it has been shewn that CA is equal to AB;
therefore CA and CB are each of them equal to AB.
But things which are equal to the same thing are equal to one another. [Axiom 1.
Therefore CA is equal to CB.
Therefore CA, AB, BC are equal to one another.
Wherefore the triangle ABC is equilateral, [Def. 24. and it is described on the given straight line AB. Q.E.F.
