PROPOSITION 18. THEOREM.
The greater side of every triangle has the greater angle opposite to it.
Let ABC be a triangle, of which the side AC is greater than the side AB: the angle ABC is also greater than the angle ACB.
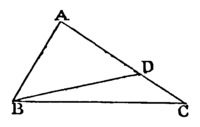
Because AC is greater than AB, make AD equal to AB, [I. 3.
and join BD.
Then, because ADB is the exterior angle of the triangle BDC, it is greater than the interior opposite angle DCB. [I. 16.
But the angle ADB is equal to the angle ABD, [I. 5.
because the side AD is equal to the side AB. [Constr.
Therefore the angle ABD is also greater than the angle ACB.
Much more then is the angle ABC greater than the angle ACB. [Axiom 9.
Wherefore, the greater side &c. q.e.d.
PROPOSITION 19. THEOREM.
The greater angle of every triangle is subtended by the greater side, or has the greater side opposite to it.
Let ABC be a triangle, of which the angle ABC is greater than the angle ACB: the side AC is also greater than the side AB.

For if not, AC must be either equal to AB or less than AB.
But AC is not equal to AB,
for then the angle ABC would be equal to the angle ACB; [I. 5.
but it is not; [Hypothesis.
therefore AC is not equal to AB. Neither is AC less than AB,
for then the angle ABC would be less than the angle ACB; [I. 18.
but it is not; [Hypothesis.
