The Elements of Euclid for the Use of Schools and Colleges/Book III
BOOK III.
DEFINITIONS.
1. Equal circles are those of which the diameters are equal, or from the centres of which the straight lines to the circumferences are equal.
This is not a definition, but a theorem, the truth of which is evident; for, if the circles be applied to one another, so that their centres coincide, the circles must likewise coincide, since the straight lines from the centres are equal.
2. A straight line is said to touch a circle, when it meets the circle, and being produced does not cut it.
3. Circles are said to touch one another, which meet but do not cut one another.
4. Straight lines are said to be equally distant from the centre of a circle, when the perpendiculars drawn to them from the centre are equal.
5. And the straight line on which the greater perpendicular falls, is said to be farther from the centre. 
6. A segment of a circle is the figure contained by a straight line and the circumference it cuts off.
7. The angle of a segment is that which is contained by the straight line and the circumference.
8. An angle in a segment is the angle contained by two straight lines drawn from any point in the circumference of the segment to the extremities of the straight line which is the base of the segment.
9. And an angle is said to insist or stand on the circumference Intercepted between the straight lines which contain the angle.
10. A sector of a circle is the figure contained by two straight lines drawn from the centre, and the circumference between them.
11. Similar segments of circles are those in which the angles are equal, or which contain equal angles.
[Note. In the following propositions, whenever the expression "straight lines from the centre," or "drawn from the centre," occurs, it is to be understood that the lines are drawn to the circumference.
Any portion of the circumference is called an arc.]
PROPOSITION 1. PROBLEM.
To find the centre of a given circle.
Let ABC be the given circle: it is required to find its centre. 
Draw within it any straight line AB and bisect AB at D; [I. 10. from the point D draw DC at right angles to AB; [I. 11. produce CD to meet the circumference at E, and bisect CE at F. [I. 10.
The point F shall be the centre of the circle ABC.
For if F be not the centre, if possible, let G be the centre; and join GA, GD, GB. Then, because DA is equal to DB, [Construction. and DG is common to the two triangles ADG, BDG; the two sides AD, DG are equal to the two sides BD, DG, each to each;
and the base GA is equal to the base GB, because they are drawn from the centre G; [I. Definition 15.
therefore the angle ADG is equal to the angle BDG. [I. 8. But when a straight line, standing on another straight line, makes the adjacent angles equal to one another, each of the angles is called a right angle; [I. Definition 10.
therefore the angle BDG is a right angle.
But the angle BDF is also a right angle. [Construction.
Therefore the angle BDG is equal to the angle BDF, [Ax.ll
the less to the greater; which is impossible.
Therefore G is not the centre of the circle ABC.
In the same manner it may be shewn that no other point out of the line CE is the centre;
and since CE is bisected at F, any other point in CE
divides it into unequal parts, and cannot be the centre.
Therefore no point but F is the centre;
that is, F is the centre of the circle ABC:
which was to he found.
PROPOSITION 2. THEOREM.
If any two points he taken in the circumference of a circle, the straight line which joins them shall fall within the circle.
Let ABC be a circle, and A and B any two points in the circumference: the straight line drawn from A to B shall fall within the circle.
For if it do not, let it fall, if possible, without, as AEB.
Find D the centre of the circle ABC; [III. 1.
and join DA, DB; in the arc AB take any point F, join DF, and produce it to meet the straight line AB at E.
Then, because DA is equal to DB, [I. Definition 15.
the angle DAB is equal to the angle DBA. [I. 5. And because AE, a side of the triangle DAE, is produced to B, the exterior angle DEB is greater than the interior opposite angle DAE. [I. 16.
But the angle DAE was shewn to be equal to the angle DBE;
therefore the angle DEB is greater than the angle DBE.
But the greater angle is subtended by the greater side; [1. 19.
therefore DB is greater than DE.
But DB is equal to DF; [I. Definition 15.
therefore DF is greater than DE, the less than the greater;
which is impossible.
Therefore the straight line drawn from A to B does not fall without the circle.
In the same manner it may be shewn that it does not fall on the circumference.
Therefore it falls within the circle.
Wherefore, if any two points &c. q.e.d.
PROPOSITION 3. THEOREM.
If a straight line drawn through the centre of a circle, bisect a straight line in it which does not pass through the centre it shall cut it at right angles; and if it cut it at right angles it shall bisect it.
Let ABC be a circle; and let CD, a straight line drawn through the centre, bisect any straight line AB, which does not pass through the centre, at the point F: CD shall cut AB at right angles.
Take E the centre of the circle; and join EA, EB.[III. 1.
Then, because AF is equal to FB, [Hypothesis.
and FE is common to the two triangles AFB, BFE;
the two sides AF, FE are equal to the two sides BF,FE, each to each;
and the base EA is equal to the base EB; [I. Def. 15.
therefore the angle AFE is equal to the angle BFE. [I. 8.
But when a straight line, standing on another straight line, makes the adjacent angles equal to one another, each of the angles is called a right angle; [I. Definition 10.
therefore each of the angles AFE, BFE is a right angle.
Therefore the straight line CD, drawn through the centre, bisecting another AB which does not pass through the centre, also cuts it at right angles.
But let CD cut AB at right angles: CD shall also bisect AB; that is, AF shall be equal to FB.
The same construction being made, because EA, EB, drawn from the centre, are equal to one another, [I. Def. 15.
the angle EAF is equal to the angle EBF. [I. 5.
And the right angle AFE is equal to the right angle BFE.
Therefore in the two triangles EAF, EBF, there are two angles in the one equal to two angles in the other, each to each;
and the side EF, which is opposite to one of the equal angles in each, is common to both;
therefore their other sides are equal; [I. 26.
therefore AF is equal to FB.
PROPOSITION 4. THEOREM.
If in a circle two straight lines cut one another, which do not both pass through the centre, they do not bisect one another.
Let ABCD be a circle, and AC, BD two straight lines in it, which cut one another at the point E, and do not both pass through the centre: AC, BD shall not bisect one another.
If one of the straight lines pass through the centre it is plain that it cannot be bisected by the other which does not pass through the centre.
But if neither of them pass through the centre, if possible, let AE be equal to EC, and BE equal to ED.
Take F the centre of the circle [III. 1.,
and join EF.
Then, because FE, a straight line drawn through the centre, bisects another straight line AC which does not pass through the centre; [Hypothesis.
FE cuts AC at right angles; ' [III. 3.
therefore the angle FEA is a right angle.
Again, because the straight line FE bisects the straight line BD, which does not pass through the centre, [Hyp.
FE cuts BD at right angles; [III. 3.
therefore the angle FEB is a right angle.
But the angle FEA was shewn to be a right angle;
therefore the angle FEA is equal to the angle FEB,[Ax.11.
the less to the greater; which is impossible.
Therefore AC, BD do not bisect each other.,
Wherefore, if in a circle &c. q.e.d.
PROPOSITION 5. THEOREM.
If two circles cut one another, they shall not have the same centre.
Let the two circles ABC, CDG cut one another at the 
points B, C: they shall not have the same centre.
For, if it be possible, let E be their centre; join EC, and draw any straight line EFG meeting the circumferences at F and G.
Then, because E is the centre of the circle ABC, EC is equal to EF. [I. Definition 15.
Again, because E is the centre of the circle CDG, EC is equal to EG. [I. Definition 15.
But EC was shewn to be equal to EF;
therefore EF is equal to EG,[Axiom 1.
the less to the greater; which is impossible.
therefore E is not the centre of the circles ABC, CDG.
Wherefore, if two circles &c. q.e.d.
PROPOSITION 6. THEOREM.
If two circles touch one another internally they shall not have the same centre.
Let the two circles ABC, CDE touch one another internally at the point G: they shall not have the same centre.
For, if it be possible, let F be their centre; join FC, and draw any straight line FEB, meeting the circumferences at E and B.
Then, because F is the centre of the circle ABC, FC is equal to FB. [I. Def. 15.
Again, because F is the centre of the circle CDE,
FC is equal to FE. [I. Definition 15.
But FC was shewn to be equal to FB
therefore FE is equal to FB,
the less to the greater; which is impossible.
Therefore F is not the centre of the circles ABC, CDE.
PROPOSITION 7. THEOREM.
If any point he taken in the diameter of a circle which is not the centre, of all the straight lines which can be drawn from this point to the circumference, the greatest is that in which the centre is, and the other part of the diameter is the least; and, of any others, that which is nearer to the straight line which passes through the centre, is always greater than one more remote; and from the same point there can he drawn to the circumference two straight lines, and only two, which are equal to one another, one on each side of the shortest line.
Let ABCD be a circle and AD its diameter, in which let any point F be taken which is not the centre; let E be the centre: of all the straight lines FB, FC, FG, &c. that can be drawn from F to the circumference, FA, which passes through E, shall be the greatest, and FD, the other part of the diameter AD, shall be the least; and of the others FB shall be greater than FC, and FC than FG.
Join BE, CE, GE.
Then, because any two sides of a triangle are greater than the third side, [I. 20.
therefore BE, EF are greater than BF.
But BE is equal to AE; [I.Def. 15.
therefore AE, EF are greater than BF,
that is, AF is greater than BF.
Again, because BE is equal to CE, [I. Definition 15.
and EF is common to the two triangles BEF, CEF;
the two sides BE, EF are equal to the two sides CE, EF, each to each;
but the angle BEF is greater than the angle CEF;
therefore the base FB is greater than the base FC. [I. 24.
In the same manner it may be shewn that FC is greater than FG.
and that EG is equal to ED; [I. Definition 15.
therefore GF, FE are greater than ED.
Take away the common part FE, and the remainder GF is greater than the remainder FD.
Therefore FA is the greatest, and FD the least of all the straight lines from F to the circumference; and FB is greater than FC, and FC than FG.
Also, there can be drawn two equal straight lines from the point F to the circumference, one on each side of the shortest line FD.
For, at the point E, in the straight line EF, make the angle FEH equal to the angle FEG, [I. 23.
and join FH.
Then, because EG is equal to EH, [I. Definition 15.
and EF is common to the two triangles GEF, HEF;
the two sides EG, EF are equal to the two sides EH, EF, each to each;
and the angle GEF is equal to the angle HEF; [Constr.
therefore the base FG is equal to the base FH. [I. 4.
But, besides FH, no other straight line can be drawn from F to the circumference, equal to FG.
For, if it be possible, let FK be equal to FG.
Then, because FK is equal to FG, [Hypothesis.
and FH is also equal to FG,
therefore FH is equal to FK; [Axiom 1.
that is, a line nearer to that which passes through the centre is equal to a line which is more remote;
which is impossible by what has been already shewn.
Wherefore, if any point be taken &c. q.e.d.
PROPOSITION 8. THEOREM.
If any point be taken without a circle, and straight lines be drawn from it to the circumference, one of which passes through the centre; of those which fall on the concave circumference, the greatest is that which passes through the centre, and of the rest, that which is nearer to the one passing through the centre is always greater than one more remote; but of those which fall on the convex circumference, the least is that between the point without the circle and the diameter; and of the rest, that which is nearer to the least is always less than one more remote; and from the same point there can he drawn to the circumference two straight lines, and only two, which are equal to one another, one on each side of the shortest line.
Let ABC be a circle, and D any point without it, and from D let the straight lines DA, DE, DF, DC be drawn to the circumference, of which DA passes through the centre: of those which fall on the concave circumference AEFC, the greatest shall be DA which passes through the centre, and the nearer to it shall be greater than the more remote, namely, DE greater than DF, and DF greater than DC;
but of those which fall on the convex circumference GKLH, the least shall be DG between the point D and the diameter AG, and the nearer to it shall be less than the more remote, namely, DK less than DL, and DL less than DH.
Take M, the centre of the circle ABC, [III. 1.
and join ME, MF, MC, MH, ML, MK.
Then, because any two sides of a triangle are greater than the third side, [I. 20.
therefore EM, MD are greater than ED.
But EM is equal to AM;[I.Def.15. therefore AM, MD are greater than ED, that is, AD is greater than ED.
Again, because EM is equal to FM,
and MD is common to the two triangles EMD, FMD;
the two sides EM, MD are equal to the two sides FM, MD, each to each;
but the angle EMD is greater than the angle FMD;
therefore the base ED is greater than the base FD. [1. 24.
In the same manner it may be shewn that FD is greater than CD.
Therefore DA is the greatest, and DE greater than DF and DF greater than DC.
Again, because MK, KD are greater than MD, [I, 20.
and MK is equal to MG [I. Definition 15.
the remainder KD is greater than the remainder GD,
that is, GD is less than KD.
And because MLD is a triangle, and from the points
M, D, the extremities of its side MD the straight lines
MK, DK are drawn to the point K within the triangle,
therefore MK, KD are less than ML, LD; [I. 21.
and MK is, equal to ML ; [I. Definition 15.
therefore the remainder KD is less than the remainder LD.
In the same manner it may be shewn that LD is less
than HD.
Therefore DG is the least, and DK less than DL, and DL
less than DH.
Also, there can be drawn two equal straight lines from the point D to the circumference, one on each side of the least line.
For, at the point M, in the straight line MD, make the
angle DMB equal to the angle DMK, [I. 23.
and join DB.
Then, because MK is equal to MB,
and MD is common to the two triangles KMD, BMD ;
the two sides KM, MD are equal to the two sides BM, MD,
each to each ;
and the angle DMK is equal to the angle DMB ; [Constr.
therefore the base DK is equal to the base DB. [I. 4.
But, besides DB, no other straight line can be drawn
from D to the circumference, equal to DK.
For, if it be possible, let DN be equal to DK.
Then, because DN is equal to DK,
and DB is also equal to DK,
therefore DB is equal to DN; [Axiom 1.
that is, a line nearer to the least is equal to one which is more remote ; which is impossible by what has been already shewn.
Wherefore, if any point be taken &c. q.e.d. PROPOSITION 9. THEOREM.
If a point be taken within a circle, from which there fall more than two equal straight lines to the circumference, that point is the centre of the circle.
Let the point D be taken within the circle ABC, from which to the circumference there fall more than two equal straight lines, namely DA, DB, DC: the point D shall be the centre of the circle.
For, if not, let E be the centre; join DE and produce it both ways to meet the circumference at F and G; then FG is a diameter of the circle.
Then, because in FG, a diameter of the circle ABC, the point D is taken, which is not the centre, DG is the greatest straight line from D to the circumference, and DC is greater than DB, and DB greater than DA; [III. 7.
but they are likewise equal, by hypothesis;
which is impossible.
Therefore E is not the centre of the circle ABC.
In the same manner it may be shewn that any other point than D is not the centre;
therefore D is the centre of the circle ABC.
Wherefore, if a point be taken &c. q.e.d.
PROPOSITION 10. THEOREM.
One circumference of a circle cannot cut another at more than two points.
If it be possible, let the circumference ABC cut the circumference DEF at more than two points, namely, at the points B, G, F.
Take K, the centre of the circle ABC, [II. 1.
and join KB, KG, KF.
Then, because K is the centre of the circle ABC,
therefore KB,KG, KF all equal to each other. [I. Def. 15.
And because within the circle DEF, the point K is taken, from which to the circumference DEF fall more than two equal straight lines KB, KG, KF, therefore K is the centre of the circle DEF. [III. 9.
But K is also the centre of the circle ABC. [Construction.
Therefore the same point is the centre of two circles which cut one another;
which is impossible. [III. 5.
Wherefore, one circumference &c. q.e.d.
PROPOSITION 11. THEOREM.
If two circles touch one another internally, the straight line which joins their centres, being produced, shall pass through the point of contact.
Let the two circles ABC, ADE touch one another internally at the point A; and let F be the centre of the circle ABC, and G the centre of the circle ADE: the straight line which joins the centres F, G, being produced, shall pass through the point A .
For, if not, let it pass otherwise, if possible, as FGDH, and join AF,AG.
Then, because AG, GF are greater than AF, [I. 20.
and AF is equal to HF, [I. Def. 15. therefore AG, GF, are greater than HF. Take away the common part GF; therefore the remainder AG is greater than the remainder HG. But AG os equal to DG. [I. Definition 15.
Therefore DG is, greater than HG, the less than the greater;
which is impossible.
Therefore the straight line which joins the points F, G, being produced, cannot pass otherwise than through the point A, that is, it must pass through A.
Wherefore, if two circles &c. q.e.d. PROPOSITION 12. THEOREM.
If two circles touch one another externally, the straight line which joins their centres shall pass through the point of contact.
Let the two circles ABC, ADE touch one another externally at the point A; and let F be the centre of the circle ABC, and G the centre of the circle ADE: the straight line which joins the points F, G, shall pass through the point A .
For, if not, let it pass otherwise, if possible, as FCDG, and join FA, AG.
Then, because F is the centre of the circle ABC, FA is equal to FC; [I.Def.16.
and because G is the centre of the circle ADE, GA is equal to GD; therefore FA, AG are equal to FC, DG. [Axiom 2.
Therefore the whole FG is greater than FA, AG. But FG is also less than FA, AG; [I. 20.
which is impossible.
Therefore the straight line which joins the points F, G, cannot pass otherwise than through the point A, that is, it must pass through A.
Wherefore, if two circles &c. q.e.d.
PROPOSITION 13. THEOREM.
One circle cannot touch another at more points than one, whether it touches it on the inside or outside.
For, if it be possible, let the circle EBF touch the circle ABC at more points than one; and first on the inside, at the points B, D. Join BD, and draw GH bisecting BD at right angles. [I. 10, 11.
Then, because the two points B, D are in the circumference of each of the circles, the straight line BD falls within each of them; [III. 2.
and therefore the centre of each circle is in the straight line GH which bisects BD at right angles; [III. 1, Corol.
therefore GH passes through the point of contact. [III. 11.
But GH does not pass through the point of contact, because the points B, D are out of the line GH;
which is absurd.
Therefore one circle cannot touch another on the inside at more points than one.
Nor can one circle touch another on the outside at more points than one.
For, if it be possible, let the circle ACK touch the circle ABG at the points A, C. Join AC.
Then, because the two points A, C are in the circumference of the circle ACK, the straight line AC which joins them, falls within the circle ACK; [III. 2.
but the circle ACK is without the circle ABC; [Hypothesis.
therefore the straight line AC is without the circle ABC.
But because the two points A,C are in the circumference of the circle ABC, the straight line AC falls within the circle ABC; [III. 2.
which is absurd.
Therefore one circle cannot touch another on the outside at more points than one.
And it has been shewn that one circle cannot touch another on the inside at more points than one.
Wherefore, one circle &c. q.e.d. PROPOSITION 14. THEOREM.
Equal straight lines in a circle are equally distant from the centre: and those which are equally distant from the centre are equal to one another.
Let the straight lines AB, CD in the circle ABDC, be equal to one another: they shall be equally distant from the centre.
Take E, the centre of the circle ABDC; [III. 1.
and from E draw EF, EG perpendiculars to AB, CD; [I. 12.
and join EA,EC.
Then, because the straight line EF, passing through the centre, cuts the straight line AB, which does not pass through the centre, at right angles, it also bisects it; [III. 3.
therefore AF is equal to FB, and AB is double of AF.
For the like reason CD is double of CG.
But AB is equal to CD; [Hypothesis.
therefore AF is equal to CG. [Axiom 7.
And because AE is equal to CE, [I. Definition 15. the square on AE is equal to the square on CE.
But the squares on AF, FE are equal to the square on AE, because the angle AFE is a right angle; [I. 47.
and for the like reason the squares on CG, GE are equal to the square on CE;
therefore the squares on AF, FE are equal to the squares on CG, GE. [Axiom 1.
But the square on AF is equal to the square on CG, because AF is equal to CG;
therefore the remaining square on FE is equal to the remaining square on GE; [Axiom 3.
and therefore the straight line EF is equal to the straight line EG.
But straight lines in a circle are said to be equally distant from the centre, when the perpendiculars drawn to them from the centre are equal; [III. Definition 4.
therefore AB, CD are equally distant from the centre.
Next, let the straight lines AB, CD be equally distant from the centre, that is, let EF be equal to EG, AB shall be equal to CD.
For, the same construction being made, it may be shewn, as before, that AB is double of AF, and CD double of CG and that the squares on EF,FA are equal to the squares on EG,GC; but the square on EF is equal to the square on EG, because EF is equal to EG; [Hypothesis. therefore the remaining square on FA is equal to the remaining square on GC, [Axiom 3.
and therefore the straight line AF is equal to the straight line CG.
But AB was shewn to be double of AF, and CD double of CG. Therefore AB is equal to CD. [Axiom 6.
Wherefore, equal straight lines &c. q.e.d.
PROPOSITION 15. THEOREM.
The diameter is the greatest straight line in a circle; and, of all others, that which is nearer to the centre is cdways greater than one more remote; and the greater is nearer to the centre than the less.
Let ABCD be a circle, of which AD is a diameter, and E the centre; and let BC be nearer to the centre than FG:
AD shall be greater than any straight line BC which is not a diameter, and BC shall be greater than FG.
From the centre E draw EH, EK perpendiculars to BC, FG, [I. 12.
and join EB, EC, EF.
Then, because AE is equal to BE, and ED to EC, [I.Def.15.
therefore AD is equal to BE, EC; [Axiom 2.
but BE, EC are greater than BC; [I. 20.
therefore also AD is greater than BC.
And, because BC is nearer to the centre than FG, [Hypothesis.
EH is less than EK. [III.Def.5.
Now it may be shewn, as in the preceding proposition, that BC is double of BH, and FG double of FK, and that the squares on EH, HB are equal to the squares on EK, KF.
But the square on EH is less than the square on EK, because EH is less than EK;
therefore the square on HB is greater than the square on KF;
and therefore the straight line BH is greater than the straight line FK;
and therefore BC is greater than FG.
Next, let BC be greater than FG: BC shall be nearer to the centre than FG, that is, the same construction being made, EH shall be less than EK.
For, because BC is greater than FG, BH is greater than FK.
But the squares on BH, HE are equal to the squares on FK,KE;
and the square on BH is greater than the square on FK;
because BH is greater than FK;
therefore the square on HE is less than the square on KE;
and therefore the straight line EH is less than the straight line EK.
Wherefore, the diameter &c. q.e.d.
PROPOSITION 16. THEOREM.
The straight line drawn at right angles to the diameter of a circle from the extremity of it, falls without the circle; and no straight line can be drawn from the extremity, between that straight line and the circumference, so as not to cut the circle. Let ABC be a circle, of which D is the centre and AB a diameter: the straight line drawn at right angles to AB, from its extremity A, shall fall without the circle.
For, if not, let it fall, if possible, within the circle, as AC, and draw DC to the point C, where it meets the circmference.
Then, because DA is equal to DC, [I. Definition 15.
the angle DAC is equal to the angle DCA. [I. 5.
But the angle DAC is a right angle; [Hypothesis.
therefore the angle DCA is a right angle;
and therefore the angles DAC, DCA are equal to two right angles; which is impossible. [I. 17.
Therefore the straight line drawn from A at right angles to AB does not fall within the circle.
And in the same manner it may be shewn that it does not fall on the circumference.
Therefore it must fall without the circle, as AE.
Also between the straight line AE and the circumference, no straight line can be drawn from the point A, which does not cut the circle.
For, if possible, let AF be between them; and from the centre D draw DG perpendicular to AF; [I. 12.
let DG meet the circumference at H.
Then, because the angle DGA is a right angle, [Construction.
the angle DAG is less than a right angle; [I. 17.
therefore DA is greater than DG. [1.19.
But DA is equal to DH; [I. Definition 15.
therefore DH is greater than DG, the less than the greater;
which is impossible.
Therefore no straight line can be drawn from the point A between AE and the circumference, so as not to cut the circle. Wherefore, the straight line &c. q.e.d.
Corollary. From this it is manifest, that the straight line which is drawn at right angles to the diameter of a circle from the extremity of it, touches the circle; [III. Def. 2. and that it touches the circle at one point only,
because if it did meet the circle at two points it would fall within it. [III. 2.
Also it is evident, that there can be but one straight line which touches the circle at the same point.
PROPOSITION 17. PROBLEM.
To draw a straight line from a given point, either without or in the circumference, which shall touch a given circle.
First, let the given point A be without the given circle BCD: it is required to draw from A a straight line, which shall touch the given circle.
Take E, the centre of the circle, [III. 1.
and join AE cutting the circumference of the given circle at D;
and from the centre E, at the distance EA, describe the circle AFG; from the point D draw DF at right angles to EA,[I.11.
and join EF cutting the circumference of the given circle at B;
join AB. AB shall touch the circle BCD.
For, because E is the centre of the circle AFG, EA is equal to EF. [I. Definition 15. And because E is the centre of the circle BCD, EB is equal to ED. [I. Definition 15.
Therefore the two sides AE, EB are equal to the two sides FE, ED, each to each;
and the angle at E is common to the two triangles AEB, FED;
therefore the triangle AEB is equal to the triangle FED, and the other angles to the other angles, each to each, to which the equal sides are opposite; [I. 4.
therefore the angle ABE is equal to the angle FDE.
But the angle FDE is a right angle; [Construction.
therefore the angle ABE is a right angle. [Axiom 1.
And EB is drawn from the centre; but the straight line drawn at right angles to a diameter of a circle, from the extremity of it, touches the circle; [III. 16, Corollary.
therefore AB touches the circle.
And AB is drawn from the given point A. q.e.f.
But if the given point be in the circumference of the circle, as the point D, draw DE to the centre E, and DF at right angles to DE; then DF touches the circle. [III. 16, Cor.
PROPOSITION 18. THEOREM.
If a straight line touch a circle the straight line drawn from the centre to the point of contact shall be perpendicular to the line touching the circle.
Let the straight line DE touch the circle ABC at the point C; take F, the centre of the circle ABC, and draw the straight line FC: FC shall be perpendicular to DE.
For if not, let FG be drawn from the point F perpendicular to DE, meeting the circumference at B.
Then, because FGC is a right angle, [Hypothesis.
FCG is an acute angle; [I. 17.
and the greater angle of every triangle is subtended by the greater side; [I. 19.
therefore FC is greater than FG.
But FC is equal to FB; [I. Definition 15.
therefore FB is greater than FG, the less than the greater;
which is impossible.
Therefore FG is not perpendicular to DE.
In the same manner it may be shewn that no other straight line from F is perpendicular to DE, but FC;
therefore FC is perpendicular to DE.
PROPOSITION 19. THEOREM.
If a straight line touch a circle, and from the point of contact a straight line he drawn at right angles to the touching line, the centre of the circle shall he in that line.
Let the straight line DE touch the circle ABC at C, and from C let CA be drawn at right angles to DE: the centre of the circle shall be in CA.
For, if not, if possible, let F be the centre, and join CF.
Then, because DE touches the circle ABC, and FC is drawn from the centre to the point of contact, FC is perpendicular to DE; [III. 18.
therefore the angle FCE is a right angle.
But the angle ACE is also a right angle; [Construction.;
therefore the angle FCE is equal to the angle ACE, [Ax.11.
the less to the greater; which is impossible. Therefore F is not the centre of the circle ABC.
In the same manner it may be shewn that no other point out of CA is the centre; therefore the centre is in CA.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 20. THEOREM.
The angle at the centre of a circle is double of the angle at the circumference on the same base, that is, on the same arc.
Let ABC be a circle, and BEC an angle at the centre, and BAC an angle at the circumference, which have the same arc, BC, for their base: the angle BEC shall be double of the angle BAC.
Join AE, and produce it to F.
First let the centre of the circle be within the angle BAC.
Then, because EA is equal to EB, the angle EAB is equal to the angle EBA; [I. 5.
therefore the angles EAB, EBA are double of the angle EAB.
But the angle BEF is equal to the angles EAB, EBA; [1. 32. therefore the angle BEF is double of the angle EAB.
For the same reason the angle FEC is double of the angle BAC.
Therefore the whole angle BEC is double of the whole angle BAC.
Next, let the centre of the circle be without the angle BAC.
Then it maybe shewn, as inthe first case, that the angle FEC is double of the angle FAC, and that the angle FEB, a part of the first, is double of the angle FAB, a part of the other;
therefore the remaining angle BEC is double of the remaining angle BAC.
Wherefore, the angle at the centre &c. q.e.d.
PROPOSITION 21. THEOREM.
The angles in the same segment of a circle are equal to one another.
Let ABGD be a circle, and BAD, BED angles in the same segment BAED: the angles BAD, BED shall be equal to one another.
Take F the centre of the circle ABGD. [III. 1.
First let the segment BAED be greater than a semicircle.
Join BF, DF.
Then, because the angle BFD is at the centre, and the angle BAD is at the circumference, and that they have the same arc for their base, namely, BCD;
therefore the angle BFD is double of the angle BAD.[III.20.
For the same reason the angle BFD is double of the angle BED.
Therefore the angle BAD is equal to the angle BED. [Ax. 7.
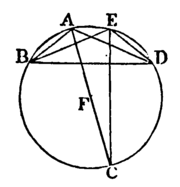Next, let the segment BAED be not greater than a semicircle.
Draw AF to the centre, and produce it to meet the circumference at C, and join CE.
Then the segment BAEC is greater than a semicircle, and therefore the angles BAC, BEC in it, are equal, by the first case. For the same reason, because the segment CAED is greater than a semicircle, the angles CAD, CED are equal.
Therefore the whole angle BAD is equal to the whole angle BED. [Axiom 2.
Wherefore, the angles in the same segment &c. q.e.d.
PROPOSITION 22. THEOREM.
The opposite angles of any quadrilateral figure inscribed in a circle are together equal to two right angles.
Let ABCD be a quadrilateral figure inscribed in the circle ABCD: any two of its opposite angles shall be together equal to two right angles.
Join AC, BD.
Then, because the three angles of every triangle are together equal to two right angles, [I. 32.
the three angles of the triangle CAB, namely, CAB, ACB, ABC are together equal to two right angles.
But the angle CAB is equal to the angle CDB, because they are in the same segment CDAB; [III. 21.
and the angle ACB is equal to the angle ADB, because they are in the same segment ADCB;
therefore the two angles CAB, ACB are together equal to the whole angle ADC. [Axiom 2.
To each of these equals add the angle ABC;
therefore the three angles CAB, ACB, ABC, are equal to the two angles ABC, ADC.
But the angles CAB, ACB, ABC are together equal to two right angles; [I. 32.
therefore also the angles ABC, ADC are together equal to two right angles.
In the same manner it may be shewn that the angles BAD, BCD are together equal to two right angles.
Wherefore, the opposite angles &c. q.e.d.
PROPOSITION 23. THEOREM.
On the same straight line, and on the same side of it, there cannot he two similar segments of circles, not coinciding with one another.
If it be possible, on the same straight line AB, and on the same side of it, let there be two similar segments of circles ACB, ADB, not coinciding with one another.
Then, because the circle ACB cuts the circle ADB at the two points A, B, they cannot cut one another at any other point; [III. 10.
therefore one of the segments must fall within the other; let ACB fall within ADB; draw the straight line BCD, and join AC, AD.
Then, because ACB, ADB are, by hypothesis, similar segments of circles, and that similar segments of circles contain equal angles, [III. Definition 11.
therefore the angle ACB is equal to the angle ADB;
that is, the exterior angle of the triangle ACD is equal to the interior and opposite angle;
which is impossible. [I. 16.
PROPOSITION 24. THEOREM.
Similar segments of circles on equal straight lines are equal to one another.
Let AEB, CFD be similar segments of circles on the equal straight lines AB, CD: the segment AEB shall be equal to the segment CFD.
For if the segment AEB be applied to the segment CFD, so that the point A may be on the point C, and the straight line AB on the straight line CD, the point B will coincide with the point D, because AB is equal to CD.
Therefore, the straight line AB coinciding with the straight line CD, the segment AEB must coincide with the segment CFD; [III. 23.
and is therefore equal to it.
Wherefore, similar segments &c. q.e.d.
PROPOSITION 25. PROBLEM.
A segment of a circle being given, to describe the circle of which it is a segment.
Let ABC be the given segment of a circle: it is required to describe the circle of which it is a segment.
Bisect AC at D; [I. 10.
from the point D draw DB at right angles to AC; [1. 11.
and join AB.
First, let the angles ABD, BAD, be equal to one another.
Then DB is equal to DA; [I. 6. but DA is equal to DC; [Construction.
therefore DB is equal to DC. [Axiom 1.
Therefore the three straight lines DA,DB,DC are all equal;
and therefore D is the centre of the circle. [III. 9.
From the centre D, at the distance of any of the three DA, DB, DC, describe a circle; this will pass through the other points, and the circle of which ABC is a segment is described.
And because the centre D is in AC, the segment ABC is a semicircle.
Next, let the angles ABD, BAD be not equal to one
another.
At the point A, in the straight line AB, make the angle
BAE equal to the angle ABD ; [I, 23.
produce BD, if necessary, to meet AE at E, and join EC.
Then, because the angle BAE is equal to the angle
ABE, [Construction.
EA is equal to EB. [I. 6.
And because AD is equal to CD, [Construction.
and DE is common to the two triangles ADE, CDE ;
the two sides AD, DE are equal to the two sides CD, DE,
each to each ;
and the angle ADE is equal to the angle CDE, for each of
them is a right angle ; [Construction.
therefore the base EA is equal to the base EC. [I. 4.
But EA was shewn to be equal to EB ;
therefore EB is equal to EC. [Axiom 1.
Therefore the three straight lines EA, EB, EC are all equal ;
and therefore E is the centre of the circle. [III. 9.
From the centre E, at the distance of any of the three EA, EB, EC, describe a circle ; this will pass through the other points, and the circle of which ABC is a segment is described.
And it is evident, that if the angle ABD be greater than the angle BAD, the centre E falls without the seg- ment ABC, which is therefore less than a semicircle ; but if the angle ABD be less than the angle BAD, the centre E falls within the segment ABC, which is therefore greater than a semicircle.
Wherefore, a segment of a circle being given, the circle has been described of which it is a segment. q.e.f. PROPOSITION 26. THEOREM.
In equal circles, equal angles stand on equal arcs, whether they be at the centres or circumferences.
Let ABC, DEF be equal circles; and let BGC, EHF be equal angles in them at their centres, and BAC, EDF equal angles at their circumferences: the arc BKC shall be equal to the arc ELF.
Join BC, EF.
Then, because the circles ABC, DEF are equal, [Hyp.
the straight lines from their centres arc equal; [III. Def. 1.
therefore the two sides BG, GC are equal to the two sides EH, HF, each to each;
and the angle at G is equal to the angle at H; [Hypothesis.
therefore the base BC is equal to the base EF. [I. 4.
And because the angle at A is equal to the angle at D,[Hyp.
the segment BAC dissimilar to the segment EDF; [III. Def. ll.
and they are on equal straight lines BC, EF.
But similar segments of circles on equal straight lines are equal to one another; [III. 24.
therefore the segment BAC be equal to the segment EDF.
But the whole circle ABC is equal to the whole circle DEF; [Hypothesis.
therefore the remaining segment BKC is equal to the remaining segment ELF; [Axiom 3.
therefore the arc BKC is equal to the arc ELF.
PROPOSITION 27. THEOREM.
In equal circles, the angles which stand on equal arcs are equal to one another whether they he at the centres or circumferences.
Let ABC, DEF be equal circles, and let the angles BGC, EHF at their centres, and the angles BAC, EDF at their circumferences, stand on equal arcs BC, EF: the angle BGC shall be equal to the angle EHF, and the angle BAC equal to the angle EDF.
If the angle BGC be equal to the angle EHF, it is manifest that the angle BAC is also equal to the angle EDF. [III. 20, Axiom 7.
But, if not, one of them must be the greater. Let BGC be the greater, and at the point G, in the straight line BG, make the angle BGK equal to the angle EHF. [I. 23.
Then, because the angle BGK is equal to the angle EHF, and that in equal circles equal angles stand on equal arcs, when they are at the centres, [III. 26.
therefore the arc BK is equal to the arc EF.
But the arc EF is equal to the arc BC; [Hypothesis.
therefore the arc BK is equal to the arc BC, [Axiom 1.
the less to the greater; which is impossible.
Therefore the angle BGC is not unequal to the angle EHF, that is, it is equal to it.
And the angle at A is half of the angle BGC, and the angle at D is half of the angle EHF; [III. 20.
therefore the angle at A is equal to the angle at D. [Ax. 7.
PROPOSITION 28. THEOREM.
In equal circles, equal straight lines cut off equal arcs, the greater equal to the greater, and the less equal to the less.
Let ABC, DEF be equal circles, and BC,EF equal straight lines in them, which cut off the two greater arcs BAC, EDF, and the two less arcs BGC, EHF the greater arc BAC shall be equal to the greater arc EDF and the less arc BGG equal to the less arc EHF.
Take K, L, the centres of the circles, [III. 1.
and join BK, KC, EL, LF.
Then, because the circles are equal, [Hypothesis. the straight lines from their centres are equal; [III. Def. 1. therefore the two sides BK, KC are equal to the two sides EL, LF, each to each;
and the base BC is equal to the base EF; [Hypothesis.
therefore the angle BKC is equal to the angle ELF. [I. 8.
But in equal circles equal angles stand on equal arcs, when they are at the centres, [III. 26.
therefore the arc BGG is equal to the arc EHF.
But the circumference ABGC is equal to the circumference DEHF; [Hypothesis. therefore the remaining arc BAC is equal to the remaining arc EDF. [Axiom 3.
Wherefore, in equal circles &c. q e.d. PROPOSITION 29. THEOREM.
In equal circles, equal arcs are subdtended by equal straight lines.
Let ABC, DEF be equal circles, and let BGG, EHF be equal arcs in them, and join BC, EF: the straight line BC shall be equal to the straight line EF.
Take K, L, the centres of the circles, [III. 1.
and join BK, KG, EL, LF.
Then, because the arc BCG is equal to the arc EHF, [Hypothesis.
the angle BKC is equal to the angle ELF. [III. 27.
And because the circles ABC, DEF are equal, [Hypothesis.
the straight lines from their centres are equal; [III. Def. 1.
therefore the two sides BK, KC are equal to the two sides EL, LF, each to each;
and they contain equal angles;
therefore the base BC is equal to the base EF. [I. 4.
Wherefore, in equal circles &c. q.e.d.
PROPOSITION 30. PROBLEM.
To bisect a given arc, that is, to divide it into two equal parts. Let ADB be the given arc: it is required to bisect it.
Join AB;
bisect it at C; [I. 10.
from the point C draw CD at right angles to AB meeting the arc at D. [I. 11
The arc ADB shall be bisected at the point D.
Join AD, DB.
Then, because AC is equal to CB, [Construction.
and CD is common to the two triangles ACD, BCD;
the two sides AC, CD are equal to the two sides BC, CD, each to each;
and the angle ACD is equal to the angle BCD, because each of them is a right angle; [Construction.
therefore the base AD is equal to the base BD. [I. 4.
But equal straight lines cut off equal arcs, the greater equal to the greater, and the less equal to the less; [III. 28.
and each of the arcs AD, DB is less than a semi-circumference, because DC, if produced, is a diameter; [III. 1. Cor. therefore the arc AD is equal to the arc DB.
Wherefore the given arc is bisected at D. q.e.f.
PROPOSITION 31. THEOREM.
In a circle the angle in a semicircle is a right angle; but the angle in a segment greater than a semicircle is less than a right angle; and the angle in a segment less than a semicircle is greater than a right angle.
Let ABCD be a circle, of which BC is a diameter and E the centre; and draw CA, dividing the circle into the segments ABC, ADC, and join BA, AD, DC: the angle in the semicircle BAC shall be a right angle; but the angle in the segment ABC, which is greater than a 
semicircle, shall be less than a right angle; and the angle in the segment ADC, which is less than a semicircle, shall be greater than a right angle.
Join AE, and produce BA to F.
Then, because EA is equal to EB, [I. Definition 15.
the angle EAB is equal to the angle EBA; [1.5.
and, because EA is equal to EC, the angle EAC is equal to the angle ECA; therefore the whole angle BAC is. equal to the two angles, ABC, ACB. [Axiom 2.
But FAC, the exterior angle of the triangle ABC, is equal to the two angles ABC, ACB; [I. 32.
therefore the angle BAC is equal to the angle FAC, [Ax. I.
and therefore each of them is a right angle. [I. Def. 10.
Therefore the angle in a semicircle BAC is a right angle.
And because the two angles ABC, BAC, of the triangle ABG, are together less than two right angles, [I. 17.
and that BAC has been shewn to be a right angle, therefore the angle ABC less than a right angle.
Therefore the angle in a segment ABC, greater than a semicircle, is less than a right angle.
And because ABCD is a quadrilateral figure in a circle, any two of its opposite angles are together equal to two right angles; [III. 22.
therefore the angles ABC, ADC are together equal to two right angles.
But the angle ABC has been shewn to be less than a right angle;
therefore the angle ADC is greater than a right angle.
Therefore the angle in a segment ADC, less than a semicircle, is greater than a right angle.
Wherefore, the angle &c. q.e.d. Corollary. From the demonstration it is manifest that if one angle of a triangle bo equal to the other two, it is a right angle.
For the angle adjacent to it is equal to the same two angles; [I. 32.
and when the adjacent angles are equal, they are right angles. [I. Definition 10.
PROPOSITION 32. THEOREM.
If a straight line touch a circle, and froam the point of contact a straight line he drawn cutting the circle, the angles which this line makes with the line touching the circle shall be equal to the angles which are in the alternate segments of the circle.
Let the straight line EF touch the circle ABCD at the point B, and from the point B let the straight line BD be drawn, cutting the circle: the angles which BD makes with the touching line EF, shall be equal to the angles in the alternate segments of the circle; that is, the angle DBF shall be equal to the angle in the segment BAD, and the angle DBE shall be equal to the angle in the segment BCD
From the point B draw BA at right angles to EF, [1. 11.
and take any point C in the, arc BD, and join AD, DC, CB.
Then, because the straight line EF touches the circle ABCD at the point B, [Hyp. and BA is drawn at right angles to the touching line from the point of contact B, [Construction.
therefore the centre of the circle is in BA. [III. 19.
Therefore the angle ADB, being in a semicircle, is a right angle. [III. 31.
Therefore the other two angles BAD, ABD are equal to a right angle. [I. 32.
But ABF is also a right angle. [Construction. Therefore the angle ABF is equal to the angles BAD, ABD.
From each of these equals take away the common angle ABD;
therefore the remaining angle DBF is equal to the remaining angle BAD, [Axiom 3.
which is in the alternate segment of the circle.
And because ABCD is a quadrilateral figure in a circle, the opposite angles BAD, BCD are together equal to two right angles. [III. 22.
But the angles DBF, DBE are together equal to two right angles. [I. 13.
Therefore the angles DBF, DBE are together equal to the angles BAD, BCD.
And the angle DBF has been shewn equal to the angle BAD;
therefore the remaining angle DBE is equal to the remaining angle BCD, [Axiom 3.
which is in the alternate segment of the circle.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 33. PROBLEM.
On a given straight line to describe a segment of a circle, containing an angle equal to a given rectilineal angle.
Let AB be the given straight line, and C the given rectilineal angle: it is required to describe, on the given straight line AB, a segment of a circle containing an angle equal to the angle C.
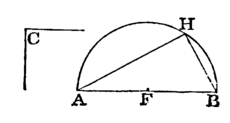First, let the angle G be a right angle.
Bisect AB at F, [1. 10.
and from the centre F, at the distance FB, describe the semicircle AHB.
Then the angle AHB in a semicircle is equal to the right angle C. [III. 31. 
But if the angle C be not a right angle, at the point A, in the straight line AB, make the angle BAD equal to the angle C; [I. 23.
from the point A, draw AE at right angles to AD;[I.ll.
bisect AB at F; [I. 10. from the point F, draw FG at right angles to AB [1. 11.
and join GB.
Then, because AF is equal to BF, [Const.
and FG is common to the two triangles AFG,BFG;
the two sides AF, FG are equal to the two sides BF, FG, each to each;
and the angle AFG is equal to the angle BFG; [I. Definition 10.
therefore the base AG is equal to the base BG; [I. 4.
and therefore the circle described from the centre G, at the distance GA, will pass through the point B.
Let this circle be described; and let it be AHB.
The segment AHB shall contain an angle equal to the given rectilineal angle G.
Because from the point A, the extremity of the diameter AE, AD is drawn at right angles to AE, [Construction.
therefore AD touches the circle. [III. 16. Corollary.
And because AB is drawn from the point of contact A, the angle DAB is equal to the angle in the alternate segment AHB. [III. 32.
But the angle DAB is equal to the angle O. [Constr.
Therefore the angle in the segment AHB is equal to the angle C. [Axiom 1.
PROPOSITION 34. PROBLEM.
From a given circle to cut off a segment containing an angle equal to a given rectilineal angle.
Let ABC be the given circle, and D the given rectilineal angle: it is required to cut off from the circle ABC a segment containing an angle equal to the angle D.
Draw the straight line BF touching the circle ABC at the point B; [III. 17.
and at the point B,in the straight line BF, make the angle FBC equal to the angle D. [I. 23.
The segment BAC shall contain an angle equal to the angle D.
Because the straight line EF touches the circle ABC, and BC is drawn from the point of contact B, [Constr.
therefore the angle FBC is equal to the angle in the alternate segment BAC of the circle. [III. 32.
But the angle FBC is equal to the angle D. [Construction.
Therefore the angle in the segment BAC is equal to the angle D. [Axiom 1.
Wherefore, from the given circle ABC, the segment BAC has been cut off, containing an angle equal to the given angle D. q.e.f.
PROPOSITION 35. THEOREM.
If two straight lines cut one another within a circle, the rectangle contained hy the segments of one of them shall be equal to the rectangle contained by the segments of the other. 
Let the two straight lines AC, BD cut one another at the point E, within the circle ABCD: the rectangle contained by AE,EC shall be equal to the rectangle contained by BE, ED.
If AC and BD both pass through the centre, so that E is the centre, it is evident, since EA, EB, EC, ED are all equal, that the rectangle AE, EC is equal to the rectangle BE,ED.
But let one of them, BD, pass through the centre, and cut the other AC, which does not pass through the centre, at right angles, at the point E. Then, if BD be bisected at F, F is the centre of the circle ABCD; join AF.
Then, because the straight line BD which passes through the centre, cuts the straight line AC, which does not pass through the centre, at right angles at the point E, [Hypothesis.
AE is equal to EC. [III. 3.
And because the straight line BD is divided into two equal parts at the point F, and into two unequal parts at the point E, the rectangle BE, ED, together with the square on EF, is equal to the square on FB, [II. 5.
that is, to the square on AF.
But the square on AF is equal to the squares on AE,EF.[l.11. Therefore the rectangle BE, ED, together with the square on EF, is equal to the squares on AE, EF. [Axiom 1.
Take away the common square on EF, then the remaining rectangle BE, ED, is equal to the remaining square on AE, that is, to the rectangle AE, EC.
Next, let BD, which passes through the centre, cut the other AC, which does not pass through the centre, at the point E, but not at right angles. Then, if BD be bisected at F, F is the centre of the circle ABCD; join AF, and from F draw FG perpendicular to AC. [I. 12.
Then AG is equal to GC; [III. 3.
therefore the rectangle AE, EC, together with the square on EG, is equal to the square on AG. [II. 5.
To each of these equals add the square on GF;
then the rectangle AE, EC, together with the squares on EG, GF, is equal to the squares on AG, GF. [Axiom 2.
But the squares on EG, GF are equal to the square on EF;
and the squares on AG, GF are equal to the square on AF. [I. 47.
Therefore the rectangle AE, EC, together with the square on EF, is equal to the square on AF,
that is, to the square on FB.
But the square on FB is equal to the rectangle BE, ED, together with the square on EF. [II. 5.
Therefore the rectangle AE, EC, together with the square on EF, is equal to the rectangle BE, ED, together with the square on EF.
Take away the common square on EF;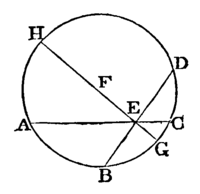
then the remaining rectangle AE, EG is equal to the remaining rectangle BE, ED. [Axiom 3.
Lastly, let neither of the straight lines AG, BD pass through the centre. Take the centre F, [III. 1.
and through E, the intersection of the straight lines AG, BD, draw the diameter GEFH.
Then, as has been shewn, the rectangle GE, EH is equal to the rectangle AE, EG, and also to the rectangle BE, ED; therefore the rectangle AE, EC is equal to the rectangle BE, ED. [Axiom 1.
PROPOSITION 36. THEOREM.
If from any point without a circle two straight lines be drawn, one of which cuts the circle, and the other touches it; the rectangle contained by the whole line which cuts the circle, and the part of it without the circle, shall be equal to the square on the line which touches it.
Let D be any point without the circle ABC, and let DCA, DB be two straight lines drawn from it, of which DCA cuts the circle and DB touches it: the rectangle AD, DC shall be equal to the square on DB.
First, let DCA pass through the centre E, and join EB. Then EBD is a right angle. [III. 18.
And because the straight line AC is bisected at E, and produced to D, the rectangle AD, DC together with the square on EC is equal to the square on ED. [II. 6.
But EC is equal to EB;
therefore the rectangle AD, DC together with the square on EB is equal to the square on ED.
But the square on ED is equal to the squares on EB, BD, because EBD is a right angle. [I. 47.
Therefore the rectangle AD, DC, together with the square on EB is equal to the squares on EB, BD.
Take away the common square on EB;
then the remaining rectangle AD, DC is equal to the square on DB. [Axiom 3.
Next let DCA not pass through the centre of the circle ABC; take the centre E; [III. 1.
from E draw EF perpendicular to AC; [I. 12.
and hoin EB,EC,ED.
Then, because the straight line EF which passes through the centre, cuts the straight line AC, which does not pass through the centre, at right angles, it also bisects it; [III. 3.
therefore AF is equal to FC.
And because the straight line AC is bisected at F, and produced to D, the rectangle AD, DC, together with the square on FC, is equal to the square on FD. [II. 6.
To each of these equals add the square on FE.
Therefore the rectangle AD, DC together with the squares on CF, FE, is equal to the squares on DF, FE. [Axiom 2.
But the squares on CF, FE are equal to the square on CE, because CFE is a right angle; [I. 47.
and the squares on DF, FE are equal to the square on DE.
Therefore the rectangle AD, DC, together with the square on CE, is equal to the square on DE.
But CE is equal to BE;
therefore the rectangle AD, DC, together with the square on BE, is equal to the square on DE.
But the square on DE is equal to the squares on DB, BE, because EBD is a right angle. [I. 47.
Therefore the rectangle AD, DC, together with the square on BE, is equal to the squares on DB, BE.
Take away the common square on BE;
then the remaining rectangle AD, DC is equal to the square on DB. [Axiom 3.
Wherefore, if from any point &c. q.e.d.
PROPOSITION 37. THEOREM.
If from any point without a circle there he drawn two straight lines, one of which cuts the circle, and the other meets it, and if the rectangle contained in the whole line which cuts the circle, and the part of it without the circle, be equal to the square on the line which meets the circle, the line which meets the circle shall touch it.
Let any point D be taken without the circle ABC, and from it let two straight lines DCA, DB be drawn, of which DCA cuts the circle, and DB meets it; and let the rectangle AD, DC bw equal to the square on DB: DB shall touch the circle.
Draw the straight line DE, touching the circle ABC [III. 17.
find F the centre, [III. 1.
and join FB, FD, FE.
Then the angle FED is a right angle. [III. 18.
And because DE touches the circle ABC, and DCA cuts it, the rectangle AD, DC is equal to the square on DE. [III. 36.
But the rectangle AD, DC is equal to the square on DB. [Hyp.
Therefore the square on DE is equal to the square on DB [Ax.1.
therefore the straight line DE is equal to the straight line DB.
And EF is equal to BF; [I. Definition 15.
therefore the two sides DE, EF are equal to the two sides DB, BF each to each;
and the base DF is common to the two triangles DEF, DBF;
therefore the angle DEF is equal to the angle DBF. [I. 8.
But DEF is a right angle; [Construction.
therefore also DBF is a right angle.
And BF, if produced, is a diameter; and the straight line which is drawn at right angles to a diameter from the extremity of it touches the circle; [III. 16. Corollary.
therefore DB touches the circle ABC.
Wherefore, if from a point &c. q.e.d.