The Elements of Euclid for the Use of Schools and Colleges/Book VI
BOOK VI.
DEFINITIONS.
 1. Similar rectilineal figures are those which have their several angles equal, each to each, and the sides about the equal angles proportionals.
1. Similar rectilineal figures are those which have their several angles equal, each to each, and the sides about the equal angles proportionals.
2. Reciprocal figures, namely, triangles and parallelograms, are such as have their sides about two of their angles proportionals in such a manner, that a side of the first figure is to a side of the other, as the remaining side of this other is to the remaining side of the first.
3. A straight line is said to be cut in extreme and mean ratio, when the whole is to the greater segment as the greater segment is to the less.
4. The altitude of any figure is the straight line drawn from its vertex perpendicular to the base. PROPOSITION 1. THEOREM.
Triangles and parallelograms of the same altitude are to one another as their bases.
Let the triangles ABC, ACD, and the parallelograms EC, CF have the same altitude, namely, the perpendicular drawn from the point A to BD: as the base BC is to the base CD, so shall the triangle ABC be to the triangle ACD and the parallelogram EC to the parallelogram CF.
 Produce BD both ways;
Produce BD both ways;
take any number of straight lines BG, GH, each equal to BC, and any number of straight lines DK, KL, each equal to CD; [I. 3.
and join AG, AH, AK, AL.
Then, because CB, BC, GH are all equal, [Construction.
the triangles ABC, AGB, AHG are all equal. [I. 38.
Therefore whatever multiple the base HC is of the base BC, the same multiple is the triangle AHC of the triangle ABC.
For the same reason, whatever multiple the base CL is of the base CD, the same multiple is the triangle ACL of the triangle ACD.
And if the base HC be equal to the base CL, the triangle AHC is equal to the triangle ACL; and if the base HC be greater than the base CL, the triangle AHC is greater than the triangle ACL; and if less, less. [I. 38.
Therefore, since there are four magnitudes, namely, the two bases BC, CD, and the two triangles ABC, ACD; and of the base BC, and the triangle ABC, the first and the third, any equimultiples whatever have been taken, namely, the base HC and the triangle AHC; and of the base CD and the triangle ACD, the second and the fourth, any equinmltiples whatever have been taken, namely, the base CL and the triangle ACL;
and since it has been shewn that if the base HC be greater
than the base CL, the triangle AHC is greater than the
triangle ACL ; and if equal, equal ; and if less, less ;
therefore as the base BC is to the base CD, so is the
triangle ABC to the triangle ACD. [V. Definition 5.
And, because the parallelogram CE is double of the
triangle ABC, and the parallelogram CF is double of the
triangle ACD; [I.41.
and that magnitudes have the same ratio which their equi-
multiples have ; [V. 15.
therefore the parallelogram EC is to the parallelogram CF
as the triangle ABC is to the triangle ACD.
But it has been shewn that the triangle ABC is to the
triangle ACD as the base BC is to the base CD ;
therefore the parallelogram EC is to the parallelogram CF
as the base BC is to the base CD. [V. 11.
Wherefore, triangles &c. q.e.d.
Corollary. From this it is plain that triangles and parallelograms which have equal altitudes, are to one an- other as their bases.
For, let the figures be placed so as to have their bases
in the same straight line, and to be on the same side of it ;
and having drawn perpendiculars from the vertices of the
triangles to the bases, the straight line which joins the ver-
tices is parallel to that in which their bases are ; [I. 33.
because the perpendiculars are both equal and parallel to
one another. [I. 28.
Then, if the same construction be made as in the pro- position, the demonstration will be the same.
PROPOSITION 2. THEOREM.
If a straight line he drawn parallel to one of the sides of a triangle, it shall cut the other sides, or those sides produced, proportionally ; and if the sides, or the sides produced, be cut proportionally, the straight line which joins the points of section, shall be parallel to the re-maining side of the triangle. Let DE be drawn parallel to BC, one of the sides of the triangle ABC: BD shall be to DA as CE is to EA.
 Join BE, CD.
Join BE, CD.
Then the triangle BDE is equal to the triangle CDE, because they are on the same base DE and between the same parallels DE, BC. [I. 37.
And ADE is another triangle;
and equal magnitudes have the same ratio to the same magnitude; [V. 7.
therefore the triangle BDE is to the triangle ADE as the triangle CDE is to the triangle ADE.
But the triangle BDE is to the triangle ADE as BD is to DA;
because the triangles have the same altitude, namely, the perpendicular drawn from E to AB, and therefore they are to one another as their bases. [VI. 1,
For the same reason the triangle CDE is to the triangle ADE as CE is to EA
Therefore BD is to DA as CE is to EA. [V. 11.
Next, let BD be to DA as CE is to EA, and join DE: DE shall be parallel to BC.
For, the same construction being made, because BD is to DA as CE is to EA, [Hypothesis.
and as BD is to DA, so is the triangle BDE to the triangle ADE, [VI. 1.
and as CE is to EA so is the triangle CDE to the triangle ADE; [VI. 1.
therefore the triangle BDE is to the triangle ADE as the triangle CDE is to the triangle ADE; [V. 11.
that is, the triangles BDE and CDE have the same ratio to the triangle ADE,
Therefore the triangle BDE is equal to the triangle CDE. [V. 9.
And these triangles are on the same base DE and on the same side of it;
but equal triangles on the same base, and on the same side of it, are between the same parallels; [I. 39.
therefore DE is parallel to BC.
Wherefore, if a straight line &c. q.e.d.
PROPOSITION 3. THEOREM.
If the vertical angle of a triangle he bisected by a straight line which also cuts the base, the segments of the base shall have the same ratio which the other sides of the triangle have to one another; and if the segments of the base have the same ratio which the other sides of the triangle have to one another, the straight line drawn from the vertex to the point of section shall bisect the vertical angle.
 Let ABC be a triangle, and let the angle BAC be bisected by the straight line AD, which meets the base at D: BD shall be to DC as BA is to AC.
Let ABC be a triangle, and let the angle BAC be bisected by the straight line AD, which meets the base at D: BD shall be to DC as BA is to AC.
Through C draw CE parallel to DA, [I. 31.
and let BA produced meet CE at E.
Then, because the straight line AC meets the parallels AD, EC, the angle ACE is equal to the alternate angle CAD; [I. 29.
but the angle CAD is, by hypothesis, equal to the angle BAD;
therefore the angle BAD is equal to the angle ACE. [Ax. 1.
Again, because the straight line BAE meets the parallels AD, EC, the exterior angle BAD is equal to the interior and opposite angle AEC; [I.29.
 but the angle BAD has been shewn equal to the angle ACE;
but the angle BAD has been shewn equal to the angle ACE;
therefore the angle ACE is equal to the angle AEC; [Axiom 1.
and therefore AC is equal to AE. [I. 6.
And, because AD is parallel to EC, [Constr.
one of the sides of the triangle BCE,
therefore BD is to DC as BA is to AE; [VI. 2.
but AE is equal to AC;
therefore BD is to DC as BA is to AC. [V.7.
Next, let BD be to DC as BA is to AC, and join AD: the angle BAC shall be bisected by the straight line AD,
For, let the same construction be made. Then BD is to DC as BA is to AC; [Hypothesis.
and BD is to DC as BA is to AE, [VI. 2.
because AD is, parallel to EC; [Construction.
therefore BA is to AC as BA is to AE; [V. 11.
therefore AC is equal to AE; [V. 9.
and therefore the angle AEC is equal to the angle ACE. [1.5.
But the angle AEC is equal to the exterior angle BAD; [1. 29.
and the angle ACE is equal to the alternate angle CAD; [1. 29.
therefore the angle BAD is equal to the angle CAD;[Ax.l.
that is, the angle BAC is, bisected by the straight line AD.
PROPOSITION A. THEOREM.
If the exterior angle of a triangle, made by producing one of its sides, be bisected by a straight line which also cuts the base produced, the segments between the dividing straight line and the extremities of the base shall have the same ratio which the other sides of the triangle have to one another; and if the segments of the base produced have the same ratio which the other sides of the triangle have to one another, the straight line drawn from the vertex to the point of section shall bisect the exterior angle of the triangle.
Let ABC be a triangle, and let one of its sides BA be produced to E; and let the exterior angle CAE be bisected by the straight line AD which meets the base produced at D: BD shall be to DC as BA is to AC.
 Through C draw CF parallel to AD, [I. 31.
Through C draw CF parallel to AD, [I. 31.
meeting AB at F.
Then, because the straight line AC meets the parallels AD, FC, the angle ACF is equal to the alternate angle CAD; [1.29.
but the angle CAD is, by hypothesis, equal to the angle DAE;
therefore the angle DAE is equal to the angle ACF. [Ax. 1.
Again, because the straight line FAE meets the parallels AD, FC, the exterior angle DAE is equal to the interior and opposite angle AFC; [I. 29.
but the angle DAE has been shewn equal to the angle ACF;
therefore the angle ACF is, equal to the angle AFC; [Ax. 1.
and therefore AC is equal to AF. [I. 6.
And, because AD is paralled to FC [Construction.
one of the sides of the triangle BCF;
therefore BD is to DC as BA is to AF; [VI. 2.
but AF is equal to AC;
therefore BD is to DC as BA is to AC [V. 7.
 Next, let BD be to DC as BA is to AC; and join AD: the exterior angle CAE shall be bisected by the straight line AD.
Next, let BD be to DC as BA is to AC; and join AD: the exterior angle CAE shall be bisected by the straight line AD.
For, let the same construction be made.
Then BD is to DC as BA is to AC; [Hypothesis.
and BD is to DC as BA is to AF; [VI. 2.
therefore BA is to DC as BA is to AF; [V. 11.
therefore AC is equal to AF [V. 9.
and therefore the angle ACF is equal to the angle AFC. [1. 5.
But the angle AFC is equal to the exterior angle DAE; [1. 29.
and the angle ACF is equal to the alternate angle CAD; [1. 29.
therefore the angle CAD is equal to the angle DAE; [Ax. 1.
that is, the angle CAE is bisected by the straight line AD.
Wherefore, if the exterior angle &c. q.e.d.
PROPOSITION 4. THEOREM.
The sides about the equal angles of triangles which are equiangular to one another are proportionals; and those which are opposite to the equal angles are homologous sides that is, are the antecedents or the consequents of the ratios.
 Let the triangle ABC be equiangular to the triangle DCE, having the angle ABC equal to the angle DCE, and the angle ACB equal to the angle DEC, and consequently the angle BAC equal to the angle CDE the sides about the equal angles of the triangles ABC, DCE, shall be proportionals; and those shall be the homologous sides, which are opposite to the equal angles.
Let the triangle ABC be equiangular to the triangle DCE, having the angle ABC equal to the angle DCE, and the angle ACB equal to the angle DEC, and consequently the angle BAC equal to the angle CDE the sides about the equal angles of the triangles ABC, DCE, shall be proportionals; and those shall be the homologous sides, which are opposite to the equal angles.
Let the triangle DCE be placed so that its side CE may be contiguous to BC, and in the same straight line with it. [I. 22.
Then the angle BCA is equal to the angle CED ; [Hyp.
add to each the angle ABC ;
therefore the two angles ABC, BCA are equal to the two angles ABC, CED ; [Axiom 2.
but the angles ABC, BCA are together less than two
right angles; [1.17.
therefore the angles ABC, CED are together less than
two right angles ;
therefore BA and ED, if produced, will meet. [Axiom 12.
Let them be produced and meet at the point F.
Then, because the angle ABC is equal to the angle
DCE, [Hypothesis.
BF is parallel to CD ; [I. 28.
and because the angle ACB Is equal to the angle DEC, [Hyp.
AC is parallel to FE. [I. 28.
Therefore FACD is a parallelogram;
and therefore AF is equal to CD, and AC is equal to FD. [1. 34.
And, because AC be parallel to FE, one of the sides of
the triangle FBE,
therefore BA is to AF as BC is to CE ; [VI. 2.
but AF is equal to CD ;
therefore BA is to CD as BC is to CE ; [V. 7.
and, alternately, AB is to BC as DC is to CE, [V. 16.
Again, because CD is parallel to BF,
therefore BC is to CE as FD is to DE ; [VI. 2.
but FD is equal to AC;
therefore BC is to CE as AC to DE ; [V. 7.
and, alternately, BC is to CA as CE is to ED. [V. 16.
Then, because it has been shewn that AB is to BC as DC
is to CE, and that DC is to CA as CE is to ED ;
therefore, ex aequali, BA is to AC as CD is to DE. [V. 22.
Wherefore, the sides &c. q.e.d.
PROPOSITION 5. THEOREM.
If the sides of two triangles, about each of their angles, be proportionals, the triangles shall be equiangular to one another, and shall have those angles equal which are opposite to the homologous sides. Let the triangles ABC, DEF have their sides proportional, so that AB is to BC as DE is to EF; and BC to CA as EF is to FD; and, consequently, ex aequali, BA to AC as ED is to DF: the triangle ABC shall be equian^ilar to the triangle DEF, and they shall have those angles equal which are opposite to the homologous sides, namely, the angle ABC equal to the angle DEF, and the angle BCA equal to the angle EFD, and the angle BAC equal to the angle EDF.
 At the point E, in the straight line EF, make the angle FEG equal to the angle ABC; and at the point F, in the straight line EF, make the angle EFG equal to the angle BCA; [I. 23.
At the point E, in the straight line EF, make the angle FEG equal to the angle ABC; and at the point F, in the straight line EF, make the angle EFG equal to the angle BCA; [I. 23.
therefore the remaining angle EGF is equal to the remaining angle BAC.
Therefore the triangle ABC is equiangular to the triangle GEF;
and therefore they have their sides opposite to the equal angles proportionals; [VI. 4.
therefore AB is to BC as GE is to EF.
But AB is to BC as DE is to EF: [Hypothesis.
therefore DE is to EF as GE is to EF; [V. 11.
therefore DE is equal to GF. [V. 9.
For the same reason, DF is equal to GF.
Then, because in the two triangles DEF, GEF, DE is equal to GE, and EF is common;
the two sides DE, EF are equal to the two sides GE, EF, each to each;
and the base DF is equal to the base GF;
therefore the angle DEF is equal to the angle GEF, [I. 8.
and the other angles to the other angles, each to each, to which the equal sides are opposite. [I. 4,
therefore the angle DFE is equal to the angle GFE, and the angle EDF is equal to the angle EGF. And, because the angle DEF is equal to the angle GEF,
and the angle GEF is equal to the angle ABC, [Constr.
therefore the angle ABC is equal to the angle DEF. [Ax. 1.
For the same reason, the angle ACB is equal to the angle
DFE, and the angle at A is equal to the angle at D.
Therefore the triangle ABC is equiangular to the triangle
DEF.
Wherefore, if the sides &c. q.e.d.
PROPOSITION 6. THEOREM.
If two triangles have one angle of the one equal to one angle of the other, and the sides about the equal angles another, and shall have those angles equal which are opposite to the homologous sides.
Let the triangles ABC, DEF have the angle BAC in the one, equal to the angle EDF in the other, and the sides about those angles proportionals, namely, BA to AC as ED is to DF: the triangle ABC shall be equiangular to the triangle DEF, and shall have the angle ABC equal to the angle DEF, and the angle ACB equal to the angle DFE.
At the point D, in the
straight line DF, make the
angle FDG equal to either
of the angles BAC, EDF ;
and at the point F, in the
straight line DF, make
the angle DFG equal to
the angle ACB; [I. 23.
therefore the remaining angle at G is equal to the remain-
ing angle at B.
Therefore the triangle ABC is equiangular to the triangle
DGF;
therefore BA is to AC as GD is to DF. [VI. 4.
But BA is to AC as ED is to DF; [Hypothesis.
therefore ED is to DF as GD is to DF; [V. 11.
therefore ED is equal to GD. [V. 9.
And DF is common to the two triangles EDF, GDF therefore the two sides ED,DF are equal to the two sides GD, DF each to each;
 and the angle EDF is equal to the angle GDF; [Constr. therefore the base EF is equal to the base GF, and the triangle EDF to the triangle GDF, and the remaining angles to the remaining angles, each to each, to which the equal sides are opposite; [I. 4.
and the angle EDF is equal to the angle GDF; [Constr. therefore the base EF is equal to the base GF, and the triangle EDF to the triangle GDF, and the remaining angles to the remaining angles, each to each, to which the equal sides are opposite; [I. 4.
therefore the angle DFG is equal to the angle DFE, and the angle at G is equal to the angle at E.
But the angle DFG is equal to the angle ACB; [Constr.
therefore the angle ACB is equal to the angle DFE. [Ax. 1.
And the angle BAC is, equal to the angle EDF; [Hypothesis.
therefore the remaining angle at B is equal to the remaining angle at E.
Therefore the triangle ABC is equiangular to the triangle DEF.
Wherefore, if two triangles &c. q.e.d.
PROPOSITION 7. THEOREM.
If two triangles have one angle of the one equal to one angle of the other, and the sides about two other angles proportionals; then if each of the remaining angles be either less, or not less, than a right angle, or if one of them he a right angle, the triangles shall he equiangular to one another, and shall have those angles equal about touch the sides are proportionals.
Let the triangles ABC, DEF have one angle of the one equal to one angle of the other, namely, the angle BAC equal to the angle EDF, and the sides about two other angles ABC, DEF, proportionals, so that AB is to BC as DE is to EF; and, first, let each of the remaining angles at C and F be less than a right angle: the triangle ABC shall be equiangular to the triangle DEF and shall have the angle ABC equal to the angle DEF, and the angle at C equal to the angle at F.
 For, if the angles ABC, DEF be not equal, one of them must be greater than the other.
For, if the angles ABC, DEF be not equal, one of them must be greater than the other.
Let ABC be the greater, and at the point B, in the straight line AB, make the angle ABC equal to the angle DEF. [I, 23.
Then, because the angle at A is equal to the angle at D, [Hyp.
and the angle ABG is equal to the angle DEF, [Constr.
therefore the remaining angle AGB is equal to the remaining angle DFE;
therefore the triangle ABG is equiangular to the triangle DEF.
Therefore AB is to BG as DE is to EF. [VI. 4.
But AB is to BG as DE is to EF; [Hypothesis.
therefore AB is to BC as AB is to BG; [V. 11.
therefore BC is equal to BG; [V. 9.
and therefore the angle BCG is equal to the angle BGC. [I. 5.
But the angle BCG is less than a right angle; [Hyp.
therefore the angle BGC is less than a right angle;
and therefore the adjacent angle AGB must be greater than a right angle. [I. 13.
But the angle AGB was shewn to be equal to the angle at F;
therefore the angle at F is greater than a right angle.
But the angle at F is less than a right angle; [Hypothesis.
which is absurd.
Therefore the angles ABC and DEF are not unequal; that is, they are equal.
And the angle at A is equal to the angle at D; [Hypothesis.
therefore the remaining angle at C is equal to the remaining angle at F;
therefore the triangle ABC is equiangular to the triangle DEF. Next, let each of the angles at C and F be not less than a right angle: the triangle ABC shall be equiangular to the triangle DEF.
 For, the same construction being made, it may be shewn in the same manner, that BC is equal to BG;
For, the same construction being made, it may be shewn in the same manner, that BC is equal to BG;
therefore the angle BCG is equal to the angle BGC. [I. 5.
But the angle BCG is not less than a right angle; [Hyp.
therefore the angle BCG is not less than a right angle; that is, two angles of the triangle BCG are together not less than two right angles; which is impossible. [I, 17.
Therefore the triangle ABC may be shewn to be equiangular to the triangle DEF, as in the first case.
Lastly, let one of the angles at C and F be a right angle, namely, the angle at C: the triangle ABC shall be equiangular to the triangle DEF.
 For, if the triangle ABC be not equiangular to the triangle DEF, at the point B, in the straight line AB, make the angle ABG equal to the angle DEF. [I. 23.
For, if the triangle ABC be not equiangular to the triangle DEF, at the point B, in the straight line AB, make the angle ABG equal to the angle DEF. [I. 23.
Then it may be shewn, as in the first case, that BC is equal to BG; therefore the angle BCG is equal to the angle BGC [I. 5.
But the angle BCG is a right angle: [Hypothesis.
therefore the angle BGC is a right angle;
that is, two angles of the triangle BCG are together equal to two right angles; which is impossible. [I. 17.
Therefore the triangle ABC is equiangular to the triangle DEF.
PROPOSITION 8. THEOREM.
In a right-angled triangle, if a perpendicular be drawn from the right angle to the base, the triangles on each side of it are similar to the whole triangle, and to one another.
Let ABC be a right-angled triangle, having the right angle BAC; and from the point A, let AD be drawn perpendicular to the base BC: the triangles DBA, DAC shall be similar to the whole triangle ABC, and to one another.
 For, the angle BAC is equal to the angle BDA, each of them being a right angle, [Axiom 11. and the angle at B is common to the two triangles ABC, DBA;
For, the angle BAC is equal to the angle BDA, each of them being a right angle, [Axiom 11. and the angle at B is common to the two triangles ABC, DBA;
therefore the remaining angle ACB is equal to the remaining angle DAB.
Therefore the triangle ABC is equiangular to the triangle DBA, and the sides about their equal angles are proportionals; [VI. 4.
therefore the triangles are similar. [VI. Definition 1.
In the same manner it may be shewn that the triangle DAC is similar to the triangle ABC.
And the triangles DBA, DAC being both similar to the triangle ABC, are similar to each other.
Wherefore, in a right-angled triangle &c. q.e.d.
Corollary. From this it is manifest, that the perpendicular drawn from the right angle of a right-angled triangle to the base, is a mean proportional between the segments of the base, and also that each of the sides is a mean proportional between the base and the segment of the base adjacent to that side.
For, in the triangles DBA, DAC,
BD is to DA as DA is to DC; [VI. 4.
and in the triangles ABC, DBA,
BC is to BA as BA is to BD; [VI. 4.
and in the triangles ABC,DAC,
PROPOSITION 9. PROBLEM.
From a given straight line to cut off any part required.
 Let AB be the given straight line: it is required to cut off any part from it.
Let AB be the given straight line: it is required to cut off any part from it.
From the point A draw a straight line AG, making any angle with AB;
in AG take any point D, and take AC the same multiple of AD, that AB is of the part which is to be cut off from it; join BC, and draw DE parallel to it. AE shall be the part required to be cut off.
For, because ED is parallel to BC, [Construction.
one of the sides of the triangle ABC,
therefore CD is to DA as BE is to EA; [VI. 2.
and, by composition, CA is to AD as BA is to AE. [V. 18.
But CA is a multiple of AD; [Construction.
therefore BA is the same multiple of AE; [V. D.
that is, whatever part AD is of AC, AE is the same part of AB.
Wherefore, from the given straight line AB, the part required has been cut off. q.e.f.
PROPOSITION 10. PROBLEM.
To divide a given straight line similarly to a given divided straight line, that is, into parts which shall have the same ratios to one another, that the parts of the given divided straight line have.
 Let AB be the straight line given to be divided, and AC the given divided straight line: it is required to divide AB similarly to AC.
Let AB be the straight line given to be divided, and AC the given divided straight line: it is required to divide AB similarly to AC.
Let AC be divided at the points D, E and let AB, AC be placed so as to contain any angle, and join BC; through the point D, draw DF parallel to BC, and through the point E draw EG parallel to BC. [I. 31.
AB shall be divided at the points F, G, similarly to AC. Through D draw DHK parallel to AB. [I. 31.
Then each of the figures FH,HB is a parallelogram; therefore BH is equal to FG, and HK is equal to GB. [1.34.
Then, because HF is parallel to KC, [Construction.
one of the sides of the triangle DKC,
therefore KH is to HD as CE is to ED. [VI. 2.
But KH is equal to BG, and HD is equal to GF; therefore BG is to GF as GE is to ED. [V. 7.
Again, because FD is parallel to GE, [Construction.
one of the sides of the triangle AGE, therefore GF is to FA as ED is to DA. [VI. 2.
And it has been shewn that BG is to GF as CE is to EB. Therefore BG is to GF as CE is to ED, and GF is to FA as ED is to BA.
Wherefore the given straight line AB is divided similarly to the given divided straight line AC. q.e.f.
PROPOSITION 11. PROBLEM.
To find a third proportional to two given straight lines.
Let AB, AC be the two given straight lines: it is required to find a third proportional to AB, AC.
 Let AB, AC be placed so as to contain any angle; produce AB, AC, to the points D, E; and make BD equal to AC; [I. 3.
Let AB, AC be placed so as to contain any angle; produce AB, AC, to the points D, E; and make BD equal to AC; [I. 3.
join BC, and through D draw DE parallel to BC. [I. 31.
CE shall be a third proportional to AB, AC.
For, because BC is parallel to BE, [Construction.
one of the sides of the triangle ABE, therefore AB is to BD as AC is to CE; [VI. 2.
but BD is equal to AC; [Construction.
therefore AB is to AC as AC is to CE. [V. 7.
PROPOSITION 12. PROBLEM.
To find a fourth proportional to three given straight lines.
Let A, B, C be the three given straight lines: it is required to find a fourth proportional to A, B, C.
 Take two straight lines, DE, DF containing any angle EDF; and in these make DG equal to A, GE equal to B, and DH equal to C; [I. 3.
Take two straight lines, DE, DF containing any angle EDF; and in these make DG equal to A, GE equal to B, and DH equal to C; [I. 3.
join GH, and through E draw EF parallel to GH. [I. 31.
HF shall be a fourth propertional to A,B,C
For, because GH is parallel to EF, [Construction.
one of the sides of the triangle DEF, therefore DG is to GE as DH is to HF. [VI. 2.
But DG is equal to A, GE is equal to B, and DH is equal to C; [Construction.
therefore A is to B as C is to HF. [V. 7.
Wherefore to the three given straight lines A, B, C, a fourth proportional HF is found, q.e.f.
PROPOSITION 13. PROBLEM.
To find a mean proportional between two given straight lines.
 Let AB, BC be the two given straight lines: it is required to find a mean proportional between them.
Let AB, BC be the two given straight lines: it is required to find a mean proportional between them.
Place AB,BC in a straight line, and on AC describe the semicircle ADC; from the point B draw BD at right angles to AC. [I. 11.
BD shall be a mean proportional between AB and BC.
Join AD, DC.
Then, the angle ADC, being in a semicircle, is a right angle; [III. 31.
and because in the right-angled triangle ADC, DB is drawn from the right angle perpendicular to the base,
therefore DB is a mean proportional between AB, BC, the segments of the base. [VI. 8, Corollary.
Wherefore, between the two given straight lines. AB, BC, a mean proportional DB is found, q.e.f.
PROPOSITION 14. THEOREM.
Equal parallelograms which have one angle of the one equal to one angle of the other, have their sides about the equal angles reciprocally proportional; and parallelograms which have one angle of the one equal to one angle of the other, and their sides about the equal angles reciprocally proportional, are equal to one another.
 Let AB, BC be equal parallelograms, which have the angle FBD equal to the angle EBG: the sides of the parallelograms about the equal angles shall be reciprocally proportional, that is, DB shall be to BE as GB is to BF.
Let AB, BC be equal parallelograms, which have the angle FBD equal to the angle EBG: the sides of the parallelograms about the equal angles shall be reciprocally proportional, that is, DB shall be to BE as GB is to BF.
Let the parallelograms be placed, so that the sides DB, BE may be in the same straight line;
therefore also FB, BG are in one straight line. [I. 14.
Complete the parallelogram FE.
Then, because the parallelogram AB is equal to the parallelogram BC, [Hypothesis.
and that FE is another parallelogram,
therefore AB is to FE as BC is to FE. [V. 7.
But AB is to FE as the base DB is to the base BE, [VI. 1.
and BC is to FE as the base GB is to the base BF; [VI. 1.
therefore DB is to BE as GB is to BF. [V. 11.
 Next, let the angle FBD be equal to the angle EBG, and let the sides about the equal angles be reciprocally proportional, namely, DB to BE as GB is to BF: the parallelogram AB shall be equal to the parallelogram BC.
Next, let the angle FBD be equal to the angle EBG, and let the sides about the equal angles be reciprocally proportional, namely, DB to BE as GB is to BF: the parallelogram AB shall be equal to the parallelogram BC.
For, let the same construction be made.
Then, because DB is to BE as GB is to BF, [Hypothesis
and that DB is to BE as the parallelogram AB is to the parallelogram FE, [VI. 1.
and that GB is to BF as the parallelogram BG is to the parallelogram 'FE'; [VI. 1.
therefore the parallelogram AB is to the parallelogram FE as the parallelogram BC is to the parallelogram FE; [V. 11.
therefore the parallelogram AB is equal to the parallelogram BC. [V. 9.
Wherefore, equal parallelograms &c. q.e.d.
PROPOSITION 15. THEOREM.
Equal triangles which have one angle of the one equal to one angle of the other, have their sides about the equal angles reciprocally proportional; and triangles which have one angle of the one equal to one angle of the other, and their sides about the equM angles reciprocally proportional, are equal to one another.
 Let ABC, ADE be equal triangles, which have the angle BAC equal to the angle DAE: the sides of the triangles about the equal angles shall be reciprocally proportional; that is, CA shall be to AD as EA is to AB.
Let ABC, ADE be equal triangles, which have the angle BAC equal to the angle DAE: the sides of the triangles about the equal angles shall be reciprocally proportional; that is, CA shall be to AD as EA is to AB.
Let the triangles be placed so that the sides CA, AD may be in the same straight line,
therefore also EA, AB are in one straight line; [1. 14.
join BD.
Then, because the triangle ABC is equal to the trian-
gle ADE, [Hypothesis.
and that ABD is another triangle,
therefore the triangle ABC is to the triangle ABD as the
triangle ADE is to the triangle ABD. [V. 7.
But the triangle ABC is to the triangle ABD as the base
CA is to the base AD, [VI. 1.
and the triangle ADE is to the triangle ABD as the base
EA is to the base AB ; [VI. 1.
therefore CA is to AD as EA is to AB. [V. 11.
Next, let the angle BAC be equal to the angle DAE, and let the sides about the equal angles be reciprocally proportional, namely, CA to AD as EA is to AB: the triangle ABC shall be equal to the triangle ADE.
For, let the same construction be made.
Then, because CA is to AD' 'as EA' 'is to AB, [Hypothesis.
and that CA is to AD as the triangle ABC is to the
triangle ABD, [VI. 1.
and that EA is to AB as the triangle ADE is to the
triangle ABD, [VI. 1.
therefore the triangle ABC is to the triangle ABD as the
triangle ADE is to the triangle ABD ; [V. 11.
therefore the triangle ABC is equal to the triangle ABD [V. 9.
Wherefore, equal triangles &c. q.e.d.
PROPOSITION 16. THEOREM.
If four straight lines he proportionals, the rectangle contained by the extremes is equal to the rectangle con-tained by the means; and if the rectangle contained by the' extremes he equal to the rectangle contained by the means, the four straight lines are proportionals. Let the four straight lines AB, CD, E, F, be proportionals, namely, let AB be to CD as E is to F: the rectangle contained by AB and F shall be equal to the rectangle contained by CD and E.

From the points A, C, draw AG, CH at right angles to AB, CD; [I. 11.
make AG equal to F, and CH equal to E; [I. 3.
and complete the parallelograms BG, DH. [I.31 .
Then, because AB is to CD as E is to F, [Hyp.
and that E is equal to CH, and F is equal to AG, [Construction.
therefore AB is to CD as CH is to AG; [V. 7.
that is, the sides of the parallelograms BG, DH about the equal angles are reciprocally proportional;
therefore the parallelogram BG is equal to the parallelogram DH. [VI. 14.
But the parallelogram BG is contained by the straight lines AB and F, because AG is equal to F, [Construction.
and the parallelogram DH is contained by the straight lines CD and E, because CH is equal to E;
therefore the rectangle contained by AB and F is equal to the rectangle contained by CD and E.
Next, let the rectangle contained by AB and F be equal to the rectangle contained by CD and E: these four straight lines shall be proportional, namely, AB shall be to CD as E is to F.
For, let the same construction be made.
Then, because the rectangle contained by AB and F is equal to the rectangle contained by CD and E, [Hypothesis.
and that the rectangle BG is contained by AB and F, because AG is equal to F, [Construction.
and that the rectangle DH is contained by CD and E, because CH is equal to E, [Construction.
[Axiom 1.therefore the parallelogram BG is equal to the parallelogram DH.
[VI. 14.And these parallelograms are equiangular to one another; therefore the sides about the equal angles are reciprocally proportional;
therefore AB is to CD as CH is to AG.
[Constr.But CH is equal to E, and AG is equal to F;
[V. 7.therefore AB is to CD as E is to F.
Wherefore, if our straight lines &c. q.e.d.
PROPOSITION 17. THEOREM.
If three straight lines he proportionals, the rectangle contained by the extremes is equal to the square on the mean; and if the rectangle contained hy the extremes he equal to the square on the mean, the three straight lines are proportionals.
Let the three straight lines A, B, C be proportionals, namely, let A be to B as B is to C: the rectangle contained by A and C shall be equal to the square on B.

Take D equal to B.
[Hyp.Then, because A is to B as B is to C,
and that B is equal to D,
[V. 7.therefore A is to B as D is to C.
[VI. 16.But if four straight lines be proportionals, the rectangle contained by the extremes is equal to the rectangle contained by the means;
therefore the rectangle contained by A and C is equal to the rectangle contained by B and D.
[Construction.But the rectangle contained by B and D is the square on B because B is equal to D;
therefore the rectangle contained by A and C is equal to the square on B.
Next, let the rectangle contained by A and C be equal to the square on B: A shall be to B as B is to C,
For, let the same construction be made.
 Then, because the rectangle contained by A and C is equal to the square on B, [Hypothesis.
Then, because the rectangle contained by A and C is equal to the square on B, [Hypothesis.
and that the square on B is equal to the rectangle contained by B and D, because B is equal to D, [Construction.
therefore the rectangle contained by A and C is equal to the rectangle contained by B and D.
But if the rectangle contained by the extremes be equal to the rectangle contained by the means, the four straight lines are proportionals; [VI. 16.
therefore A is to D as B is to C.
But B is equal to D; [Construction.
Therefore A is to B as B is to C. [V. 7.
Wherefore, if three straight lines &c. q.e.d.
PROPOSITION 18. PROBLEM.
On a given straight line to describe a rectilineal figure similar and similarly situated to a given rectilineal figure.
 Let AB be the given straight line, and CDEF the given rectilineal figure of four sides: it is required to describe on the given straight line AB, a, rectilineal figure, similar and similarly situated to CDEF.
Let AB be the given straight line, and CDEF the given rectilineal figure of four sides: it is required to describe on the given straight line AB, a, rectilineal figure, similar and similarly situated to CDEF.
Join DF at the point A, in the straight line AB, make the angle BAC equal to the angle; and at the point B, in the straight line AB, make the angle ABG equal to the angle CDF;[I.23.
therefore the remaining angle AGB is equal to the remain-
ing angle CFD,
and the triangle AGB is equiangular to the triangle CFD,
Again, at the point B, in the straight line BG, make the
angle GBH equal to the angle FDE; and at the point G,
in the straight line BG, make the angle BGH equal to
the angle DFE; [1.23.
therefore the remaining angle BHG is equal to the re-
maining angle DEF,
and the triangle BHG is equiangular to the triangle DEF.
Then, because the angle AGB is equal to the angle CFD,
and the angle BGH equal to the angle DFE; [Construction.
therefore the whole angle AGH is equal to the whole
angle CFE. [Axiom 2.
For the same reason the angle ABH is equal to the
angle CDE.
And the angle BAG is equal to the angle DCF, and the
angle BHG is equal to the angle DEF.
Therefore the rectilineal figure ABHG is equiangular to
the rectilineal figure CDEF.
Also these figures have their sides about the equal angles proportionals.
For, because the triangle BAC is equiangular to the triangle
DCF, therefore BA to AC as DC is to CF. [VI. 4.
And, for the same reason, AC is to GB as CF is to FD,
and BC is to GH as DF is to FE ;
therefore, ex aequali, AG is to GH as CF is to FB. [V. 22.
In the same manner it may be shewn that AB is to BH
as CD is to DE.
And GH is to HB as FE is to ED. [VI. 4.
Therefore, the rectilineal figures ABHG and CDEF are equiangular to one another, and have their sides about the equal angles proportionals ; therefore they are similar to one another. [VI. Definition 1.
Next, let it be required to describe on the given straight
line AB, a rectilineal figure, similar, and similarly situated,
to the rectilineal figure CDKEF of five sides.
 Join DE, and on the given straight line AB describe, as in the former case, the rectilineal figure ABHG, similar, and similarly situated to the rectilneal figure CDEF of four sides. At the point B in the straight line BH, make the angle HBL equal to the angle EDK and at the point H, in the straight line BH make the angle BHL equal to the angle DEK; [I. 23.
Join DE, and on the given straight line AB describe, as in the former case, the rectilineal figure ABHG, similar, and similarly situated to the rectilneal figure CDEF of four sides. At the point B in the straight line BH, make the angle HBL equal to the angle EDK and at the point H, in the straight line BH make the angle BHL equal to the angle DEK; [I. 23.
therefore the remaining angle at L is equal to the remaining angle at K.
Then, because the figures ABHG, CDEF are similar, the angle ABH is equal to the angle CDE; [VI. Def. 1.
and the angle HBL is equal to the angle EDK [Constr.
therefore the whole angle ABL is equal to the whole angle CDK, [Axiom 2.
For the same reason the whole angle GHL is equal to the whole angle FEK.
Therefore the five-sided figures ABHG and CDKEF are equiangular to one another.
And, because the figures ABHG and CDEF are similar, therefore AB is to BH as CD is to DE [VI. Definition 1.
but BH is to BL as DE is to DK; [VI. 4.
therefore, ex aequali, AB is to BL as CD is to DK. [V. 22.
For the same reason, GH is to HL as FE is to EK.
And BL is to LH as DK is to KE. [VI. 4.
Therefore, the five-sided figures ABLHG and CDKEF are equiangular to one another, and have their sides about the equal angles proportionals;
therefore they are similar to one another. [VI. Definition 1.
PROPOSITION 19. THEOREM.
Similar triangles are to one another in the duplicate ratio of their homologous sides.
 Let ABC and DEF be similar triangles, having the angle B equal to the angle E, and let AB be to BC as DE is to EF so that the side BC is homologous to the side EF: the triangle ABC shall be to the triangle DEF in the duplicate ratio of BC to EF.
Let ABC and DEF be similar triangles, having the angle B equal to the angle E, and let AB be to BC as DE is to EF so that the side BC is homologous to the side EF: the triangle ABC shall be to the triangle DEF in the duplicate ratio of BC to EF.
Take BG a third proportional to BG and EF, so that BG may be to EF as EF is to BG; [VI. 11.
and join AG.
Then, because AB is to BC as DE is to EF, [Hypothesis.
therefore, alternately, AB is to DE as C is to EF; [V. 16.
but BC is to EF as EF is to BG; [Construction.
therefore AB is to DE as EF is to BG; [V. 11.
that is, the sides of the triangles ABG and DEF, about their equal angles, are reciprocally proportional;
but triangles which have their sides about two equal angles reciprocally proportional are equal to one another, [VI. 15.
therefore the triangle ABG is equal to the triangle DEF.
And, because BG is to EF as EF is to BG,
therefore BG has to BG the duplicate ratio of that which BC has to EF. [V. Definition 10.
But the triangle ABC is to the triangle ABG as BC is to BG; [VI. 1.
therefore the triangle ABC has to the triangle ABG the duplicate ratio of that which BC has to EF. But the triaingle ABG was shewn equal to the triangle DEF;
therefore the triangle ABC has to the triangle DEF the duplicate ratio of that which BC has to EF. [V. 7.
Wherefore, similar triangles &c. q.e.d.
Corollary. From this it is manifest, that if three straight lines be proportionals, as the first is to the third, so is any triangle described on the first to a similar and similarly described triangle on the second.
PROPOSITION 20. THEOREM.
Similar polygons may he divided into the same number of similar triangles, having the same ratio to one another that the polygons have; and the polygons are to one another in the duplicate ratio of their homologous sides.
Let ABCDE, FGHKL be similar polygons, and let AB be the side homologous to the side FG: the polygons ABCDE, FGHKL may be divided into the same number of similar triangles, of which each shall have to each the same ratio which the polygons have; and the polygon ABCDE shall be to the polygon FGHKL in the duplicate ratio of AB to FG.
Join BE, EC, GL, LH.
Then, because the polygon ABCDE is similar to the polygon FGHKL, [Hypothesis.
the angle BAE is equal to the angle GFL, and BA is to AE as GF is to FL. [VI. Definition 1.
And, because the triangles ABE and FGL have one angle of the one equal to one angle of the other, and the sides
 about these equal angles proportionals,
about these equal angles proportionals,
therefore the triangle ABE is equiangular to the triangle FGL, [VI. 6.
and therefore these triangles are similar; [VI. 4.
therefore the angle ABE is equal to the angle FGL.
But, because the polygons are similar, [Hypothesis.
therefore the whole angle ABC is equal to the whole angle
FGH, [VI. Definition 1.
therefore the remaining angle EBC is equal to the remain-
ing angle LGH. [Axiom 3.
And, because the triangles ABE and FGL are similar,
therefore EB is to BA as LG is to GF;
and also, because the polygons are similar, [Hypothesis.
therefore AB is to BC as FG is to GH ; [VI. Definition 1.
therefore, ex aequali, EB is to BC as LG is to GH; [V. 22.
that is, the sides about the equal angles EBC and LGH
are proportionals ;
therefore the triangle EBC is equiangular to the triangle
LGH; [VI. 6.
and therefore these triangles are similar. [VI. 4.
For the same reason the triangle ECD is similar to the
triangle LHK.
Therefore the similar polygons ABCDE, FGHKL may be
divided into the same number of similar triangles.
Also these triangles shall have, each to each, the same ratio which the polygons have, the antecedents being ABE, EBC, ECD, and the consequents FGL, LGH, LHK; and the polygon ABCDE shall be to the polygon FGHKL in the duplicate ratio of AB to FG.
For, because the triangle ABE is similar to the tri-
angle FGL,
therefore ABE is to FGL in the duplicate ratio of EB
to LG. [VI. 19.
For the same reason the triangle EBC is to the triangle
LGH in the duplicate ratio of EB to LG.
Therefore the triangle ABE is to the triangle FGL as the
triangle EBC is to the triangle LGH. [V. 11.
Again, because the triangle EBC is similar to the tri-
angle LGH,
therefore EBC is to LGH in the duplicate ratio of EC
to LH. [VI. 19.
For the same reason the triangle ECD is to the triangle LHK in the duplicate ratio of EC to LH.
Therefore the triangle EBC is to the triangle LGH as the triangle ECD is to the triangle LHK. [V. 11.
But it has been shewn that the triangle EBC is to the triangle LGH as the triangle ABE is to the triangle FGL.
Therefore as the triangle ABE is to the triangle FGL, so is the triangle EBC to the triangle LGH, and the triangle ECD to the triangle LHK; [V. 11.
and therefore as one of the antecedents is to its consequent so are all the antecedents to all the consequents; [V. 12.
that is, as the triangle ABE is to the triangle FGL so is the polygon ABCDE to the polygon FGHKL.
But the triangle ABE is to the triangle FGL in the duplicate ratio of the side AB to the homologous side FG; [VI. 19.
therefore the polygon ABCDE is to the polygon FGHKL in the duplicate ratio of the side AB to the homologous side FG.
Wherefore, similar polygons &c. q.e.d.
Corollary 1. In like manner it may be shewn that similar four- sided figures, or figures of any number of sides, are to one another in the duplicate ratio of their homologous sides; and it has already been shewn for triangles; therefore universally, similar rectilineal figures are to one another in the duplicate ratio of their homologous sides.
Corollary 2. If to AB and FG, two of the homologous sides, a third proportional M be taken, [VI. 11.
 then AB has to M the duplicate ratio of that which AB has to FG. [V. Definition 10.
then AB has to M the duplicate ratio of that which AB has to FG. [V. Definition 10.
But any rectilineal figure described on 'AB' is to the similar and similarly described rectilineal figure on FG in the duplicate ratio of AB to FG, [Corollary 1.
Therefore as AB is to M, so is the figure on AB to the figure on FG; [V. 11.
and this was shewn before for triangles. [VI. 19, Corollary.
Wherefore, universally, if three straight lines be propor-tionals, as the first is to the third, so is any rectilineal figure described on the first to a similar and similarly described rectilineal figure on the second.
PROPOSITION 21. THEOREM.
Rectilineal figures which are similar to the same rectilineal figure, are also similar to each other.
Let each of the rectilineal figures A and B be similar to the rectilineal figure C: the figure A shall be similar to the figure B.
 For, because A is similar to C, [Hyp.
For, because A is similar to C, [Hyp.
A is equiangular to C, and A and C have their sides about the equal angles proportionals. [VI. Def. 1.
Again, because B is similar to C, [Hyp.
B is equiangular to C, and B and C have their sides about the equal angles proportionals. [VI. Definition 1.
Therefore the figures A and B are each of them equiangular to C, and have the sides about the equal angles of each of them and of C proportionals.
Therefore A is equiangular to B, [Axiom 1.
and A and B have their sides about the equal angles proportionals; [V. 11
therefore the figure A is similar to the figure B. [VI. Def. 1.
PROPOSITION 22. THEOREM.
If four straight lines he proportionals, the similar rectilineal figures similarly described on them shall also be proportionals; and if the similar rectilineal figures similarly described on four straight lines be proportionals, those straight lines shall be proportionals.
Let the four straight lines AB, CD, EF, GH be proportionals, namely, AB to CD as EF is to GH;
and on AB, CD let the similar rectilineal figures KAB, LCD be similarly described;
and on EF, GH let the similar rectilineal figures MF, NH be similarly described:
the figure KAB shall be to the figure LCD as the figure MF is to the figure NH.
 To AB and CD take a third proportional X, and to EF and GH a third proportional O. [VI. 11.
To AB and CD take a third proportional X, and to EF and GH a third proportional O. [VI. 11.
Then, because AB is to CD as EF is to GH, [Hypothesis.
and AB is to CD as CD is to X; [Construction.
and EF is to GH as GH is to O; [Construction.
therefore CD is to X as GH is to O. [V. 11.
And AB is to CD as EF is to GH;
therefore, ex æquali, AB is to X as EF is to O. [V. 22.
But as AB is to X, so is the rectilineal figure KAB to the rectilineal figure LCD; [VI. 20, Corollary 2.
and as EF is to O, so is the rectilineal figure MF to the rectilineal figure NH; [VI. 20, Corollary 2.
therefore the figure KAB is to the figure LCD as the
figure MF is to the figure NH. [V. 11.
Next, let the figure KAB be to the similar figure LCD as the figure MF is to the similar figure NH; AB shall be to CD as EF is to GH.
Make as AB is to CD so EF to PR : [VI. 12.
and on PR describe the rectilineal figure SR, similar and
similarly situated to either of the figures MF, NH. [VI, 18.
Then, because AB is to CD as EF is to PR,
and that on AB, CD are described the similar and simi-
larly situated rectilineal figures KAB, LCD,
and on EF, PR the similar and similarly situated recti-
lineal figures MF, SR ;
therefore, by the former part of this proposition, KAB is
to LCD as MF is to SR.
But, by hypothesis, KAB is to LCD as MF is to NH;
therefore MF is to SR as MF is to NH ; [V. 11.
therefore SR is equal to NH. [V. 9.
But the figures SR and NH are similar and similarly
situated, [Construction.
therefore PR is equal to GH.
And because AB is to CD as EF is to PR,
and that PR is equal to GH ;
therefore AB is to CD as EF is to GH. [V. 7.
Wherefore, if four straight lines &c. q.e.d.
PROPOSITION 23. THEOREM.
Parallelograms with are equiangular to one another have to one another the ratio which is compounded of the ratios of their sides. Let the parallelogram AC be equiangular to the parallelogram CF, having the angle BCD equal to the angle ECG: the parallelogram AC shall have to the parallelogram CF the ratio which is compounded of the ratios of their sides.
 Let BC and CG be placed in a straight line;
Let BC and CG be placed in a straight line;
therefore DC and CE are also in a straight line; [I. 1 4,
complete the parallelogram DG;
take any straight line K, and make K to L as BC is to CG and L to M as DC to CE; [VI 12.
then the ratios of K to L and of L to M are the same with the ratios of the sides, namely, of BC to CG and of DC to CE.
But the ratio of K to M is that which is said to be compounded of the ratios of K to L and of L to M; [V. Def. A.
therefore K has to M the ratio which is compounded of the ratios of the sides.
Now the parallelogram AC is to the parallelogram CH as BC is to CG; [VI. 1.
but BC is to CG as ^is to Z; [Construction.
therefore the parallelogram AC is to the parallelogram CH as Kis to L. [V. 11.</br Again, the parallelogram CH is to the parallelogram CF as DC is to CE; [VI 1.
but DC is to CE as L is to M; [Construction.
therefore the parallelogram CH is to the parallelogram CF as L is to M. [V. 11.
Then, since it has been shewn that the parallelogram AC is to the parallelogram CH as K is to L,
and that the parallelogram CH is to the parallelogram CF as L is to M,
therefore, ex sequali, the parallelogram AC is to the parallelogram CF as K is to M. [V. 22. But K has to M the ratio which is compounded of the ratios of the sides;
therefore also the parallelogram AC has to the parallelogram CF the ratio which is compounded of the ratios of the sides.
Wherefore, parallelograms &c. q.e.d.
PROPOSITION 24. THEOREM.
Parallelograms about the diameter of any parallelogram are similar to the whole parallelogram and to one another.
Let ABCD be a parallelogram, of which AC is a diameter; and let EG and HK be parallelograms about the diameter: the parallelograms EG and HK shall be similar both to the whole parallelogram and to one another.
 For, because DC and GF are parallels,
For, because DC and GF are parallels,
the angle ADC is equal to the angle AGF. [I. 29.
And because BC and EF are parallels, the angle ABC is equal to the angle AEF. [I. 29.
And each of the angles BCD and EFG is equal to the opposite angle BAD, [I. 34.
and therefore they are equal to one another.
Therefore the parallelograms ABCD and AEFG are equiangular to one another.
And because the angle ABC is equal to the angle AEF, and the angle BAC is common to the two triangles BAC and EAF,
therefore these triangles are equiangular to one another; and therefore AB is to BC as AE is to EF. [VI. 4.
And the opposite sides of parallelograms are equal to one another;
therefore AB is to AD as AE is to AG,
and DC is to CB as GF is to FE,
and CD is to DA as FG is to GA.[V.7
Therefore the sides of the parallelograms ABCD and AEFG about their equal angles are proportional,
and the parallelograms are therefore similar to one another. [VI. Definition 1.
 For the same reason the parallelogram ABCD is similar to the parallelogram FHCK.
For the same reason the parallelogram ABCD is similar to the parallelogram FHCK.
Therefore each of the parallelograms EG and HK is similar to BD;
therefore the parallelogram EG is similar to the parallelogram HK.
Wherefore, parallelograms &c. q.e.d.
PROPOSITION 25. PROBLEM.
To describe a rectilineal figure which shall he similar to one given rectilineal figure and equal to another given rectilineal figure.
Let ABC be the given rectilineal figure to which the figure to be described is to be similar, and D that to which it is to be equal: it is required to describe a rectilineal figure similar to ABC and equal to D.

On the straight line BC describe the parallelogram BE equal to the figure ABC.
On the straight line CE describe the parallelogram CM equal to D, and having the angle FCE equal to the angle CBL; [I. 45, Corollary.
therefore BC and CF will be in one straight line, and LE and EM will be in one straight line.
Between BC and CF find a mean proportional GH, [VI. 13.
and on GH describe the rectilineal figure KGH, similar and similarly situated to the rectilineal figure ABC. [VI. 18.
KGH shall be the rectilineal figure required.
For, because BG is to GH as GH is to GF, [Construction.
and that if three straight lines be proportionals, as the first is to the third so is any figure on the first to a similar and similarly described figure on the second, [VI. 20, Cor. 2.
therefore as BC is to GF so is the figure ABC to the figure KGH.
But as BC is to CF so is the parallelogram BE to the parallelogram CM; [VI. 1.
therefore the figure ABG is to the figure KGH as the parallelogram BE is to the parallelogram GM. [V. 11.
And the figure ABG is equal to the parallelogram BE;
therefore the rectilineal figure KGH is equal to the parallelogram GM. [V. 14.
But the parallelogram GM is equal to the figure D; [Constr.
therefore the figure KGH is equal to the figure D, [Axiom 1.
and it is similar to the figure ABG. [Construction.
Wherefore the rectilineal figure KGH has heen de-scribed similar to the figure ABC, and equal to D. q.e.f.
PROPOSITION 26. THEOREM.
If two similar parallelograms have a common angle, and be similarly situated, they are about the same diameter.
 Let the parallelograms ABCD, AEFG be similar and similarly situated, and have the common angle BAD: ABCD and AEFG shall be about the same diameter.
Let the parallelograms ABCD, AEFG be similar and similarly situated, and have the common angle BAD: ABCD and AEFG shall be about the same diameter.
For, if not, let, if possible, the parallelogram BD have its diameter AHC in a different straight line from AF, the diameter of the prallelogram EG; let GF meet AHC at H, and through H draw HK parallel to AD or BC. [1. 31.
 Then the parallelograms ABCD and AKHG are about the same diameter, and are therefore similar to one another; [VI. 24.
Then the parallelograms ABCD and AKHG are about the same diameter, and are therefore similar to one another; [VI. 24.
therefore DA is to AB as GA is to AK.
But because ABCD and AEFG are similar parallelograms, [Hypothesis.
therefore DA is to AB as GA is to AE. [VI. Definition 1.
Therefore GA is to AK as GA is to AE, [V. 11. that is, GA has the same ratio to each of the straight lines AK and AE,
and therefore AK is equal to AE, [V. 9.
the less to the greater; which is impossible.
Therefore the parallelograms ABCD and AEFG must have their diameters in the same straight line, that is, they are about the same diameter.
Wherefore, if two similar parallelograms &c. q.e.d.
PROPOSITION 30. PROBLEM.
To cut a given straight line in extreme and mean ratio.
Let AB be the given straight line: it is required to cut it in extreme and mean ratio.
![]() Divide AB at the point C, so that the rectangle contained by AB, BC may be equal to the square on AC. [II.11.
Divide AB at the point C, so that the rectangle contained by AB, BC may be equal to the square on AC. [II.11.
Then, because the rectangle AB, BC is equal to the square on AC, [Construction.
therefore AB is to AC a,s AC is to CB. [VI. 17.
PROPOSITION 31. THEOREM.
In any right-angled triangle, any rectilineal figure described on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.
Let ABC be a right-angled triangle, having the right angle BAC: the rectilineal figure described on BC shall be equal to the similar and similarly described figures on BA and CA.
 Draw the perpendicular AD. [I. 12.
Draw the perpendicular AD. [I. 12.
Then, because in the rightangled triangle ABC, AD is drawn from the right angle at A, perpendicular to the base BC, the triangles ABD, CAD are similar to the whole triangle CBA,and to one another. [VI. 8.
And because the triangle CBA is similar to the triangle ABD,
therefore CB is to BA as BA is to BD. [VI. Def. 1.
And when three straight lines are proportionals, as the first is to the third so is the figure described on the first to the similar and similarly described figure on the second; [VI. 20, Corollary 2.
therefore as CB is to BD so is the figure described on CB to the similar and similarly described figure on BA;
and inversely, as BD is to BC so is the figure described on BA to that described on CB. [V. B.
In the same manner, as CD is to CB so is the figure described on CA to the similar figure described on CB.
Therefore as BD and CD together are to CB so are the figures described on BA and CA together to the figure described on CB. [V. 24.
Cut BD and CD together are equal to CB;
therefore the figure described on BC is equal to the similar and similarly described figures on BA and CA. [V. A.
PROPOSITION 32. THEOREM.
If two triangles, which have two sides of the one pro- portional to two sides of the other, he joined at one angle so as to have their homologous sides parallel to one another, the remaining sides shall he in a straight line.
Let ABC and DCE be two triangles, which have the two sides BA, AC proportional to the two sides CD, DE, namely, BA to AC as CD is to DE and let AB be parallel to DC and AC parallel to DE: BC and CE shall be in one straight line.
 For, because AB is parallel to DC, [Hypothesis.
For, because AB is parallel to DC, [Hypothesis.
and AC meets them, the alternate angles BAC, ACD are equal; [I. 29.
for the same reason the angles ACD, CDE are equal;
therefore the angle BAC is equal to the angle CDE. [Ax. 1.
And because the triangles ABC, DCE have the angle at A equal to the angle at D, and the sides about these angles proportionals, namely, BA to AC as CD is to DE, [Hyp.
therefore the triangle ABC is equiangular to the triangle DCE; [VI. 6.
therefore the angle ABC is equal to the angle DCE.
And the angle BAC was shewn equal to the angle ACD;
therefore the whole angle ACE is equal to the two angles ABC and BAC. [Axiom 2.
Add the angle ACB to each of these equals;
then the angles ACE and ACB are together equal to the angles ABC, BAC, ACB.
But the angles ABC, BAC, ACB are together equal to two right angles; [I. 32.
therefore the angles ACE and ACB are together equal to two right angles.
And since at the point C, in the straight line AC, the two straight lines BC, CE which are on the opposite sides of it, make the adjacent angles ACE,ACB together equal to two right angles,
therefore BC and CE are in one straight line. [I. 14.
Wherefore, if two triangles &c. q.e.d.
PROPOSITION 33. THEOREM.
In equal circles, angles, whether at the centres or at the circumferences, have the same ratio which the arcs on which they stand have to one another; so also have the sectors.
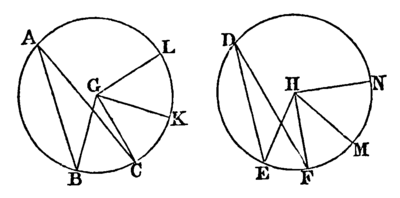
Let 'ABC and BEF be equal circles, and let BGC and EHF be angles at their centres, and BAC and EDF angles at their circumferences: as the arc BC is to the arc EF so shall the angle BGC be to the angle EHF, and the angle BAC to the angle EDF; and so also shall the sector BGC be to the sector EHF.
Take any number of arcs CK, KL, each equal to BC, and also any number of arcs FM, MN each equal to EF; and join GK, GL, HM, HN.
Then, because the arcs BC, CK, KL, are all equal, [Constr.
the angles BCG, CGK, KGL are also all equal; [III. 27.
and therefore whatever multiple the arc BL is of the arc BC, the same multiple is the angle BGL of the angle BGC.
For the same reason, whatever multiple the arc EN is of the arc EF, the same multiple is the angle EHN of the angle EHF.
And if the arc BL be equal to the arc EN, the angle BGL is equal to the angle EHN; [III. 27.
and if the arc BL be greater than the arc EN, the angle BGL is greater than the angle EHN; and if less, less.
Therefore since there are four magnitudes, the two arcs BC,EF, and the two angles BGC, EHF;
 and that of the arc BC and of the angle BGC have been taken any equimultiples whatever, namely, the arc BL and the angle BGL;
and that of the arc BC and of the angle BGC have been taken any equimultiples whatever, namely, the arc BL and the angle BGL;
and of the arc EF and of the angle EHF have been taken any equimultiples whatever, namely, the arc EN and the EHN;
and since it has been shewn that if the arc BL be greater than the arc EN, the angle BGL is greater than the angle EHN; and if equal, equal; and if less, less;
therefore as the arc BC is to the arc EF, so is the angle BGC to the angle EHF. [V. Definition 5.
But as the angle BGC is to the angle EHF, so is the angle BAC to the angle EDF, [V. 15.
for each is double of each; [III. 20.
therefore, as the arc BC is to the arc EF so is the angle BGC to the angle EHF, and the angle BAC to the angle EBF.
Also as the arc BC is to the arc EF, so shall the sector BGC be to the sector EHF.
Join BC, CK, and in the arcs BC, CK take any points X, O, and join BX, XC, CO, OK.
Then, because in the triangles BGC,CGK the two sides BG, GC are equal to the two sides CG, GK, each to each;
and that they contain equal angles; [III. 27.
therefore the base BC is equal to the base CK, and the triangle BGC is equal to the triangle CGK, [I. 4.
 And because the arc BC is equal to the arc CK, [Constr.
And because the arc BC is equal to the arc CK, [Constr.
the remaining part when BC is taken from the circumference is equal to the remaining part when CK is taken from the circumference;
therefore the angle BXC is equal to the angle COK. [III. 27.
Therefore the segment BXC is similar to the segment COK; [III. Definition 11.
and they are on equal straight lines BC, CK.
But similar segments of circles on equal straight lines are equal to one another; [III. 24.
therefore the segment BXC is equal to the segment COK.
And the triangle BGC was shewn to be equal to the triangle CGK;
therefore the whole, the sector BGC, is equal to the whole, the sector CGK [Axiom 2.
For the same reason the sector KGL is equal to each of the sectors BGC, CGK,
In the same manner the sectors EHF, FHM, MHN may be shewn to be equal to one another.
Therefore whatever multiple the arc BL is of the arc BC, the same multiple is the sector BGL of the sector BGC;
and for the same reason whatever multiple the arc EN is of the arc EF the same multiple is the sector EHN of the sector EHF.
And if the arc BL be equal to the arc EN the sector BGL is equal to the sector EHN;
and if the arc BL be greater than the arc EN the sector BGL is greater than the sector EHN; and if less, less.
Therefore, since there are four magnitudes, the two arcs BC, EF, and the two sectors BGC, EHF;
 and that of the arc BC and of the sector BGC have been taken any equimultiples whatever, namely, the arc BL and the sector BGL;
and that of the arc BC and of the sector BGC have been taken any equimultiples whatever, namely, the arc BL and the sector BGL;
and of the arc EF and of the sector EHF have been taken any equimultiples whatever, namely, the arc EN and the sector BGL;
and since it has been shewn that if the arc BL be greater than the arc EN, the sector BGL is greater than the sector EHN; and if equal, equal; and if less, less;
therefore as the arc BC is to the arc EF, so is the sector BGC to the sector EHF. [V. Definition 5.
PROPOSITION B. THEOREM.
If the vertical angle of a triangle be bisected by a straight line which likewise cuts the base, the rectangle contained by the sides of the triangle is equal to the rectangle con-tained by the segments of the base, together with the square on the straight line which bisects the angle.
Let ABC be a triangle, and let the angle BAC be bisected by the straight line AD: the rectangle BA, AC shall be equal to the rectangle BD,DC, together with the square on AD.
 Describe the circle ACB about the triangle, [IV. 5.
Describe the circle ACB about the triangle, [IV. 5.
and produce AD to meet the circumference at E,
and join EC.
Then, because the angle BAD is equal to the angle EAC, [Hypothesis.
and the angle ABD is equal to the angle ABC, for they are in the same segment of the circle, [III. 21.
therefore the triangle BAD is equiangular to the triangle EAC.
Therefore BA is to AD as BA is to AC; [VI. 4.
therefore the rectangle BA, AC is equal to the rectangle EA,AD, [VI. 16.
that is, to the rectangle BD, DA, together with the square on AD. [II. 3,
But the rectangle JSD, DA is equal to the rectangle BD,DC; [III.35.
therefore the rectangle BA, AC is equal to the rectangle BD, DC, together with the square on AD.
PROPOSITION C. THEOREM.
If from the vertical angle of a triangle a straight line, be drawn perpendicular to the base, the rectangle contained by the sides of the triangle is equal to the rectangle con-tained by the perpendicular and the diameter of the circle described about the triangle.
Let ABC be a triangle, and let AD be the perpendicular from the angle A to the base BC the rectangle BA, AC shall be equal to the rectangle contained by AD and the diameter of the circle described about the triangle.
 Describe the circle ACB about the triangle; [IV. 5.
Describe the circle ACB about the triangle; [IV. 5.
draw the diameter AE, and join EC
Then, because the right angle BDA is equal to the angle ECA in a semi-circle; [III. 31.
and the angle ABD is equal to the angle AEC, for they are in the same segment of the circle; [III. 21.
therefore the triangle ABD is equiangular to the triangle AEC.
Therefore BA is to AD as EA is to AC; [VI; 4.
therefore the rectangle BA, AC is equal to the rectangle EA,AD. [ VI. 16.
Wherefore, if from the vertical angle &c. q.e.d.
PROPOSITION D. THEOREM.
The rectangle contained by the diagonals of a quadrilateral figure inscribed in a circle is equal to both the rectangles contained by its opposite sides. Let ABCD be any quadrilateral figure inscribed in a circle, and join AC,BD: the rectangle contained by AC, BD shall be equal to the two rectangles contained by AB,CD and AD,BC.
 Make the angle ABE equal to the angle DBC; [I. 23.
Make the angle ABE equal to the angle DBC; [I. 23.
add to each of these equals the angle EBD,
then the angle ABD is equal to the angle EBC. [Axiom 2.
And the angle BDA is equal to the angle BCE, for they are in the same segment of the circle; [III.21.
therefore the triangle ABD is equiangular to the triangle EBC.
Therefore AD is to DB as EC is to CB; [VI. 4.
therefore the rectangle AD, CB is equal to the rectangle DB, EC. [VI. 16.
Again, because the angle ABE is equal to the angle DBC, [Construction.
and the angle BAE is equal to the angle BDC, for they are in the same segment of the circle; [III. 21.
therefore the triangle ABE is equiangular to the triangle DBC.
Therefore BA is to AE as BD is to DC; [VI. 4.
therefore the rectangle BA, DC is equal to the rectangle AE, BD. [VI. 16.
But the rectangle AD, CB has been shewn equal to the rectangle DB, EC;
therefore the rectangles AD, CB and BA, DC are together equal to the rectangles BD, EC and BD, AE;
that is, to the rectangle BD, AC. [II. 1.
Wherefore, the rectangle contained &c. q.e.d.

