The Mathematical Principles of Natural Philosophy (1729)/Book 1/Section 11

Section XI.
Of the motions of bodies tending to each other with centripetal forces.
I have hitherto been treatin of the attractions of bodies towards an immoveable centre; tho' very probably there is no such thing existent in nature. For attractions are made towards bodies; and the actions of the bodies attracted and attracting, are always reciprocal and equal by law 3. s that if there are two bodies neither the attracted nor the attracting body is truly at rest, but both (by cor. 4. of the laws of motion) being as it were mutually attracted, revolve about a common centre of gravity. And if there be more bodies, which are either attracted by one single one which is attracted by them again, or which, all of them, attract each other mutually; these bodies will be so moved among themselves, as that their common centre of gravity will either be at rest, or move uniformly forward in a right line. I shall therefore at present go on to treat of the motion of bodies mutually attracting each other; considering the centripetal forces as attractions; though perhaps in a physical strictness they may more truly be called impulses. But these propositions are to be considered as purely mathematical; and therefore laying aside all physical considerations, I make use of a familiar way of speaking, to make my self the more easily understood by a mathematical reader.
Proposition LVII. Theorem XX.
Two bodies attracting each other mutually, describe similar figures about their common centre of gravity, and about each other mutually.
For the distances of the bodies from their common
centre of gravity are reciprocally as the bodies;
and therefore in a given ratio to each other;
and thence by composition of ratio's, in a given
ratio the whole distance between the bodies.
Now these distances revolve about their common
term with an equable angular motion, because lying
in the same right line they never change their
inclination to each other mutually. But right lines
that are in a given ratio to each other, and revolve
about their terms with an equal angular motion, describe
upon planes, which either rest with those
terms, or move with any motion not angular, figures
entirely similar round those terms. Therefore the
figures described by the revolution of these distances
are similar. Q. E. D.
Proposition LVIII. Theorem XXI.
If two bodies attract each other mutually with forces of any kind, and in the mean time revolve about the common centre of gravity; I say that by the same forces there may be described round either body unmoved, a figure similar and equal to the figure are which the bodies so moving describe round each other mutually.

Let the bodies S and P (Pl. 20. Fig. 7.) revolve about their common centre of gravity C. proceeding from S to T and from P to Q From the given point s, let there be continually drawn sp, sq, equal and parallel to SP, TQ and the curve pqv, which the point p describes in its revolution round the immovable point s, will be similar and equal to the curves, which the bodies S and P describe about each other mutually; and therefore by theor. 20. similar to the curves ST and PQV which the same bodies describe about their common centre of gravity C; and that because the proportions of the lines SC, CP, and SP or sp, to each other, are given.
Case 1.. The common centre of gravity C (by cor. 4 of the laws of motion) is either at rest, or moves uniformly in a right line. Let us first suppose it at rest, and in s and p let there be placed two bodies, one immovable in s, the other moveable in p, similar and equal to the bodies S and P. Then let the right lines PR and pr touch the curves PQ and pq in P and p, and produce CQ and sq to R and r. And because the figures CPRQ, sprq are similars, RQ will be to rq as CP to sp, and therefore in a given ratio. Hence if the force with which the body P is attracted towards the body S, and by consequence towards the intermediate point the centre C, were to the force with which the body p is attracted towards the centre s, in the same given ratio; these forces would in equal times attract the bodies from the tangents PR, pr to the arcs PQ, pq, through the intervals proportional to them RQ, rq; and therefore this last force (tending to s) would make the body p revolve in the curve pqv, which would become similar to the curve PQV, in which the first force obliges the body P to revolve; and their revolutions would be compleated in the same times. But because those forces are not to each other in the ratio of CP to sp, but (by reason of the similarity and equality of the bodies S and s, P and p, and the equality of the distances SP, sp) mutually equal; the bodies in equal times will be equally drawn from the tangents; and therefore that the body p may be attracted through the greater interval rq, there is required a greater time, which will be in the subduplicate ratio of the intervals; because by lemma 10, the spaces described at the very beginning of the motion are in a duplicate ratio of the times. Suppose then the velocity of the body p to be to the velocity of the body P in a subduplicate ratio of the distance sp to the distance CP, so that the arcs pq, PQ, which are in a simple proportion to each other, may be described in times that are in a subduplicate ratio of the distances; and the bodies P, p, always attracted by equal forces will describe round the quiescent centres C and s similar figures PQV, pqv, the latter of which pqv is similar and equal to the figure which the body P describes round the moveable body. Q. E. D.
Case 2. Suppose now that the common centre of gravity together with the space in which the bodies are moved among themselves, proceeds uniformly in a right line; and (by cor. 6. of the laws of motion) all the motions in this space will be performed in the same manner as before; and therefore the bodies will describe mutually about each other the same figures as before, which will be thererefore similar and equal to the figure pqv. Q. E. D.
Cor. 1. Hence two bodies attracting each other with forces proportional to their distance. describe (by prop. 10.) both round their common centre of gravity, and round each other mutually, concentrical ellipses; and vice versa if such figures are described, the forces are proportional to the distances.
Cor. 2. And two bodies, whose forces are reciprocally proportional to the square of their distance describe, (by prop. 11, 12, 13.) both round their common centre of gravity and round each other mutually, conic sections having their focus in the centre about which the figures are described And vice versa, if such figures are described, the centripetal forces are reciprocally proportional to the square of the distance.
Cor. 3.. Any two bodies revolving round their common centre of gravity, describe areas proportional to the times, by radii drawn both to that centre and to other mutually.
Proposition LIX. Theorem XXII.
The periodic time of two bodies S and P revolving round their common centre of gravity C, is to the periodic time of one of the bodies P revolving round the other S remaining unmoved and describe a figure similar and equal to those which the bodies describe about each other mutually, in a subduplicate ratio of the other body S to the sum of the bodies S + P.
For by the demonstration of the last proposition,
the times in which any similar arcs PQ
and pq are described, are in a subduplicate ratio
of the distances CP and SP or sp, that is in it
subduplicate ratio of the body S to the sum of
the bodies S + P. And by composition of ratio's
the fums of the times in which all the similar
arcs PQ, and pq are described, that is, the whole
times in which the whole similar figures are described, are in the same subduplicate ratio. Q. E. D.
Proposition LX. Theorem XXIII.
If two bodies S and P, attracting each other with forces reciprocally proportional to the squares of their distance, revolve about their common centre of gravity; I say that the principal axis of the ellipsis which either of the bodies as P describesr by this motion about the other S, will be to the principal axis of the ellipsis, which the same body P may describe in the same periodical time about the other body S quiescent, as the sum of the two bodies S + P to the first of two mean proportionals between that sum and the other body S.
For if the ellipses described were equal to each other, their periodic times by the last theorem would be in a subduplicate ratio of the body S to the sum of the bodies S + P. Let the periodic time in the latter ellipsis be diminished in that ratio, and the periodic times will become equal; but by prop. 15. the principal axis of the ellipsis will be diminished in a ratio sesquiplicate to the former ratio; that is in a ratio, to which the ratio of S to S + P is triplicate; and therefore that axis will be to the principal axis of the other ellipsis. as the first of two mean proportionals between S + P and S to S + P. And inversely the principal axis of the ellipsis described about the moveable body, will be to the Principal axis of that described round the immoveable, as S + P to the first of two mean proportionals between S + P and S. Q. E. D.
Proposition LXI. Theorem XXIV.
If two bodies attracting each other with any kind of forces, and not otherwise agitated or obstructed, are moved in any manner whatsoever; those motion: will he the same, as if they did not at all attract each other mutually, but were both attracted with the same forces by a third body placed in their common centre of gravity; and the law of the attracting forces will be the same in respect of the distance of the bodies from the the common centre, as in respect of the distance between the two bodies.
For those forces with which the bodies attract
each other mutually, by tending to the bodies tend
also to the common centre of gravity lying directly
between them; and therefore are the same
as if they proceeded from an intermediate body.
Q. E. D.
And because there is given the ratio of the distance
of either body from that common centre to
the distance between the two bodies, there is given
of course the ratio of any power of one distance
to the same power of the other distance;
and also the ratio of any quantity derived in any
manner from one of the distances compounded any
how with given quantities, to another quantity, derived
in like manner from the other distance, and
as many given quantities having that given ratio
of the distances to the first. Therefore if the
force with which one body is attracted by another
be directly or inversely as the distance of the
bodies from each other, or as any power of that
distance; or lastly as any quantity derived after any
manner from that distance compounded with
given quantities; then will the same force with
which the same body is attracted to the common
centre of gravity, be in like manner directly or
inversely as the distance of the attracted body from
the common centre, or as any power of that distance,
or lastly as a quantity derived in like fort
from that distance compounded with analogous
given quantities. That is, the law of attracting
force will be the same with respect to both distances.
Q. E. D.
Proposition LXII. Problem XXXVIII.
To determine the motions of two bodies which attract each other with forces reciprocally proportional to the squares of the distance between them, and are let fall from given places.
The bodies, by the last theorem, will be moved in the same manner as if they were attracted by a third placed in the common centre of their gravity; and by the hypothesis that centre will quiescent at the beginning of their motion, and therefore (by cor. 4. of the laws of motion) will be always quiescent. The motions of the bodies are therefore to be determined (by Prob. 25.) in the same manner as if they were impelled by forces tending to that centre; and then we shall have the motions of the bodies attracting each other mutually. Q. E. I.
Proposition LXIII. Problem XXXIX.
To determine the motion: of two bodies attracting each other with forces reciprocally proportional to the squares of their distance, and going off from given places in given directions, with given velocities.
The motions of the bodies at the beginning being given, there is given also the uniform motion of the common centre of gravity, and the motion of the space which moves along with this centre uniformly in a right line, and also the very first, or beginning motions of the bodies in respect of this space. Then (by cor. 5. of the laws, and the last theorem) the subsequent motions will be performed in the same manner in that space, as if that space together with the common centre of gravity were at rest, and as if the bodies did not attract each other; but were attracted by a third body placed in that centre. The motion therefore in this moveable space of each body going off from a given place, in a given direction, with a given velocity, and acted upon by a centripetal force tending to that centre, is to be determined by prob. 9. and 26. and at the same time will be obtained the motion of the other round the same centre. With this motion compound the uniform progressve motion of the entire system of the space and the bodies revolving in it, and there will be obtained the absolute motion of the bodies in immovable space. Q. E. I.
Proposition LXIV. Problem XL.
Supposing forces with which bodies mutually attract each other to increase in a simple ratio of their distances from the centres; it it required to find the motions of several bodies among themselves.

Suppose the two first bodies T and L (Pl. 21. Fig. 1.) to have their common centre of gravity in D. These by cor. 1. theor. 21. will describe ellipses having their centres in D, the magnitudes of which ellipses are known by prob. 5.
Let now a third body S attract the two former T and L with the accelerative forces ST, SL, and lee it be attracted again by them. The force ST (by cor. 2. of the laws of motion) is resolved into the forces SD, DT; and the force SL into the forces SD and DL. Now the forces DT, DL, which are as their sum TL, and therefore as the accelerative forces with which the bodies T and L attract each other mutually, added to the forces of the bodies T and L, the first to the first, and the last to the last, compose forces proportional to the distances DT and DL as before, but only greater than those former forces; and therefore (by cor. 1. prop. 10. and cor. 1. and 8. prop. 4.) they will cause those bodies to describe ellipses as before, but with a swifter motion. The remaining accelerative forces SD and SD, by the motive forces, SD x T and SD x L which are as the bodies, attracting those bodies equally, and in the direction of the lines TI, LK parallel to DS, do not at all change their situations with respect to one another, but cause them equally to approach to the line IK; which must be imagined drawn through the middle of the body S, and perpendicular to the line DS. But that approach to the line IK will be hindered by causing the system of the bodies T and L on one side, and the body S on the other with proper velocities to revolve round the common centre of gravity C. With such a motion the body S, because the sum of the motive forces SD x T and SD x L is proportional to the distance CS, tends to the centre C, will describe an ellipsis round the same centre C; and the point D, because the lines CS and CD are proportional, will describe a like ellipsis over-against: it. But the bodies T and L, attracted by the motive forces SD x T and SD x L, the first by the first, and the last by the last equally and in the direction of the parallel lines TI and LK as was said before. will (by cor. 5. and 6. of the laws of motion) continue to describe their ellipses round the moveable centre D as before. Q. E. I.
Let there be added a fourth body V, and by the like reasoning it will be demonstrated that this body and the point C will describe ellipses about the common centre of gravity B; the motions of the bodies T, L and S round the centres D and C remaining the same as before; but accelerated. And by the same method one may add yet more bodies at pleasure. Q. E. I.
This would be the case, though the bodies T
and L artract each other mutually with accelerative
forces either greater or less than those with
which they attract the other bodies in proportion
to their distance. Let all the mutual accelerative
attractions be to each other as the distances multiplyed
into the attracting bodies; and from what has gone
before it will easily be concluded that all the bodies
will describe different ellipses with equal periodical
times about their common centre of gravity B, in
an immoveable plane. Q. E. I.
Proposition LXV. Theorem XXV.
Bodies, whose forces decrease in a duplicate ratio of their differences from their centres, may move among themselves in ellipsis; and by radii drawn to the foci may describe area's proportional to the time very nearly.
In the last proposition we demonstrated that case in which the motions will be performed exactly in ellipses. The more distant the law of the forces is from the law in that case, the more will the bodies disturb each others motions; neither is it possible that bodies attracting each other mutually according to the law supposed in this proposition should move exactly in ellipses unless keeping a certain proportion of distances from each other. However in the following cases the orbits will not much differ from ellipses.
Case 1. Imagine several lesser bodies to revolve about some very great one at different distances from it, and suppose absolute forces tending to every one of the bodies, proportional to each. And because (by cor. 4. of the laws) the common centre of gravity of them all is either at rest or moves uniformly forward in a right line, suppose the lesser bodies so small that the great body may be never at a sensible distance from that centre; and then the great body will, without any sensible error, be either at rest or move uniformly forward in a right line; and the lesser will revolve about that great one in ellipses, and by radii drawn thereto will describe areas proportional to the times; if we except the errors that may be introduced by the receding of the great body from the common centre of gravity, or by the mutual actions of the lesser bodies upon each other. But the lesser bodies may be so far diminished, as that this recess and the mutual actions of the bodies on each other may become less than any assignable and therefore so as that the orbits may come ellipses, and the areas answer to the times, without any error that is not less than any assignable. Q. E. O.
Case 2. Let us imagine a systemp of lesser bodies revolving about a very great one in the manner described, or any other system of two bodies revolving about each other to be moving uniformly forward in a right line, and in the mean time to impelled side-aways by the force of another vastly greater body situate at a great distance. And because the equal accelerative forces with which the bodies are impelled in parallel directions do not change the situation of the bodies with respect to each other, but only oblige the whole system to change its place while the parts still retain their motions among themselves; it is manifest, that no change in those motions of the attracted bodies can arise from their attractions towards the greater, unless by the inequality of the accelerative attractions, or by the inclinations of the lines towards each other, in whose directions the attractions are made. Suppose therefore all the accelerative attractions made towards the great body to be among themselves as the squares of the distances reciprocally; and then, by increasing the distance of the great body till the differences of the right lines drawn from that to the others in respect of their length, and the inclinations of those lines to each other, be less than any given, the motions of the parts of the system will continue without errors that are not less than any given. And because by the small distance of those parts from each other, the whole system is attracted as if it were but one body, it will therefore be moved by this attraction as if it were one body; that is, its centre of gravity will describe about the great body one of the conic sections (that is, a parabola or hyperbola when the attraction is but languid, and an ellipsis when it is more vigorous) and by radii drawn thereto it will describe area's proportional to the times, without any errors but those which arise from the distances of the parts, which are by the supposition exceeding small, and may be diminished at pleasure. Q. E. O.
By a like reasoning one may proceed to more compounded cases in infinitum.
Cord 1. In the second case, the nearer the very great body approaches to the system of two or more revolving bodies, the greater will the perturbation be of the motions of the parts of the system among themselves; because the inclinations of the lines drawn from that great body to those parts become greater; and the inequality of the proportion is also greater.
Cor 2. But the perturbation will be greatest of all, if we suppose the accelerative attractions of the parts of the system towards the greatest body of all are not to each other reciprocally as the squares of the distances from that great body; especially if the inequality of this proportion be greater than the inequality of the proportion of the distances from the great body. For if the accelerative force, acting in parallel directions and equally, causes no perturbation in the motions of the parts of the system, it must of course, when it acts unequally, cause a perturbation somewhere, which will be greater or less as the inequality is greater or less. The excess of the greater impulses acting upon some bodies, and not acting upon others, must necessarily change their situation among themselves. And this perturbation, added to the perturbation arising from the inequality and inclination of the lines, makes the whole perturbation greater.
Cor. 3. Hence if the parts of this system move in ellipses or circles without any remarkable perturbation; it is manifest, that if they are at all impelled by accelerative forces tending to any other bodies, the impulse is very weak, or else is impressed very near equally and in parallel directions upon all of them,
Proposition LXVI. Theorem XXVI.
If three bodies whose forces decrease in a duplicate ratio of the distances, attract each other mutually; and the accelerative attractions of any two towards the third be between themselves reciprocally as the squares of the distances and the two leass revolve about the greatest; I say that the interior of the two revolving bodies will, by radii drawn to the innermost and greatest, describe round that body, area's more proportional to the times, and a figure more approaching to that of an ellipssis having its focus in the point of concourse of the radii, if that great body be agitated by those attraction, than it would do if that great body were not attracted at all by the lesser, but remained at rest; or than it would if that great body were very much more much less attracted, or very much more or very much less agitated by the attractions.
This appears plainly enough from the demonstration of the second corollary of the foregoing proposition; but it may be made out after this manner by a way of reasoning more distinct and more universally convincing.
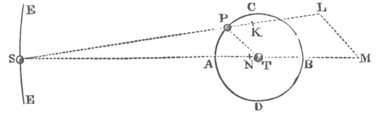
Case 1. Let the lesser bodies P and S (Pl. 21. Fig. 2.) revolve in the same plane about the greatest body T, the body P describing the interior orbit PAB, and S the exterior orbit ESE, Let SK be the mean distance of the bodies P and S; and let the accelerative attraction of the body P towards S, at that mean distance, be expressed by that line SK. Make SL to SK as the square of SK to the square of SP, and SL will be the accelerative attraction of the body P towards S at an distance SP. Join PT and draw LM parallel to it meeting ST in M; and the attraction SL will be resolved (by cor. 2. of the laws of motion) into the attractions SM, LM. And so the body P will be urged with a threefold accelerative force. One of these forces tends towards T; and arises from the mutual attraction of the bodies T and P. By this force alone the body P would describe round the body T; by the radius PT, areas proportional to the times, and an ellipsis whose focus is in the centre of the body T; and this it would do whether the body T remained unmoved, or whether it were agitated by that attraction. This appears from prop. 11. and cor. 2 & 3 of theor. 21. The other force is that of the attraction LM, which because it tends from P to T will be super-added to and coincide with the former force; and cause the area's to be still proportional to the times, by cor. 3. theor. 21. But because it is not reciprocally proportional to the square of the distance PT, it will compose when added to the former, a force varying from proportion; which variation will be the greater, by how much the proportion of this force to the former is greater, cæteris paribus. Therefore since by prop. 11. and by cor. 2. theor. 21. the force with which the ellipsis is described about the focus T ought to be directed to that focus; and to be reciprocally proportional to the square of the distance PT; that compounded force varying from that proportion will make the orbit PAB vary from the figure of an ellipsis that has its focus in the point T; and so much the more by how much the variation from that proportion is greater and by consequence by how much the proportion of the second force LM to the first force is greater, cæteris paribus. But now the third force SM, attracting the body P in a direction parallel to ST; composes with the other forces a new force which is no longer directed from P to T; and which varies so much more from this direction, by how much the proportion of this third force to the other forces is greater cæteris paribus; and therefore causes the body P to describe, by the radius TP, area's no longer proportional to the times; and therefore makes the variation from that proportionality so much greater by how much the proportion of this force to the others is greater. But this third force will increase the variation of the orbit PAB from the elliptical figure before mentioned upon two accounts; first because that force is not directed from P to T; and secondly because it is not reciprocally proportional to the square of the distance PT. These things being premised, it is manifest, that the area's are then most nearly proportional to the times, when that third force is the least possible, the rest preserving their former quantity; and that the orbit PAB does then approach nearest to the elliptical figure above-mentioned, when both the second and third, but especially the third force, is the least possible; the first force remaining in its former quantity.
Let the accelerative attraction of the towards S be expressed by the line SN; then if the accelerative attractions SM and SN were equal, these, attracting the bodies T and P equally and in parallel directions, would not at all change their situation with respect to each other. The motions of the bodies between themselves would be the same in that case as if those attractions did not act at all. by cor. 6. of the laws of motion. And by a like reasoning if the attraction SN is less than the attraction SM, it will take away out of the attraction SM the part SN, so that there will remain only the part (of the attraction) MN, to disturb the proportionality of the area's and times, and the elliptical figure of the orbit. And in like manner if the attraction SN be greater than the attraction SM, the perturbation of the orbit and proportion will be produced by the difference MN alone. After this manner the attraction SN reduces always the attraction SM to the attraction MM the first and second attractions perfectly unchanged; and therefore the area's and times come then nearest to proportionality, and the orbit PAB to the above-mentioned elliptical figure, when the attraction MN is either none, or the least that is possible; that is, when the accelerative attractions of the bodies P and T approach as near as possible to equality; that is, when the attraction SN is neither none at all, nor less than the least of all the attractions SM, but is as it were a mean between the greatest and least of all those attractions SM. that is, not much greater nor much less than the attraction SK. Q. E. D.
Case 2. Let now the lesser bodies P, S, revolve about a greater T in different planes; and the force LM acting in the direction of the line PT situate in the plane of the orbit PAB, will have the same effect as before; neither will it draw the body P from the plane of its orbit. But the other force NM acting in the direction of a line parallel to ST (and which therefore what the body S is without the line of the nodes in inclined to the plane of the orbit PAB) besides the perturbation of the motion just now spoken of as to longitude. introduces another perturbation also as to latitude, attracting the body P out of the plane of its orbit. And this perturbation, in any given situation of the bodies P and T to each other, will be as the generating force MN; and therefore becomes least when the force MN is least, that is, (as was just now shewn) where the attraction 5N is not much greater nor much less than the attraction SK. Q. E. D.
Cor. 1.. Hence it may be easily collected, that if several less bodies P, S, R, &c. revolve about a very great body T; the motion of the innermost revolving body P will be least disturbed by the attractions of the others. when the great body is as well attracted and agitated by the rest (according to the ratio of the accelerative forces) as the rest are by each other mutually.
Cor. 2. In a system of three bodies T, P, S, if the accelerative attractions of any two of them towards a third be to each other reciprocally as the squares of the distances; the body P, by the radius PT; will describe its area swifter near the conjunction A and the opposition B, than it will near the quadratures C and D. For every force with which the body P is acted on and the body T is not, and which does not act in the direction of the line PT; does either accelerate or retard the description of the area, according as it is directed, whether in consequentia or in antecedentia. Such is the force NM. This force in the passage of the body P from C to A is directed in consequentia to its motion, and therefore accelerates it; then as far as D in antecedentia, and retards the motion; then in consequentia as far as B; and lastly in antecedentia as it moves from B to C.
Cor. 3. And from the same reasoning it appears that the body P, cæteris paribus, moves more swiftly in the conjunction and opposition than in the quadratures.
Cor. 4 The orbit of the body P, cæteris paribus, is more curve at the quadratures than at the conjunction and opposition. For the swifter bodies move, the less they deflect from a rectilienar path. And besides the force KL, or NM, at the conjunction and opposition, is contrary the force with which the body T attracts the body P; and therefore diminishes that force; but the body P will deflect the less from a rectilinear path the less it is impelled towards the body T.
Cor. 5 Hence the body P cæteris paribus goes farther from the body T at the quadratures than at the conjunction and opposition. This is said however, supposing no regard had to the motion of eccentricity. For if the orbit of the body P be eccentrical, its eccentricity (as will be shewn presently by cor. 9.) will be greatest when the apsides are in the syzygies; and thence it may sometimes comme to pass, that the body P in its near approach to the farther apsis, may go farther from the body T at the syzygies, than at the quadratures.
Cor. 6. Because the centripetal force of the central body T, by which the body P is retained in its orbits, is increased at the quadratures by the addition caused by the force LM, and diminished at the syzigies by the subduction caused by the force KL; and by reason the force KL is greater than LM is more diminished than increased; and moreover since that centripetal force (by cor. 1. prop. 4.) is in a ratio compounded of the simple ratio of the radius TP directly, and the duplicate ratio of the periodical time inversely; it is plain that this compounded ratio is diminished by the action of the force KL; and therefore that the periodical time, supposing the radius of the orbit PT to remain the same, will be increased. and that in the subduplicate of that ratio in which the centripetal force is diminished and therefore supposing this radius increased or diminished, the periodical time will be increased more or diminished less than in the sesquiplicate ratio of this radius, by cor. 6. prop. 4. If that force of the central body should gradually decay, the body P being less an less attracted would go farther and farther from the centre T; and on the contrary if it were increased it would draw nearer to it. Therefore if the action of the distant body S, by which that force is diminished, were to increase and decrease by turns; the radius TP will be also increased and diminished by turns; and the periodical time will be increased and diminished in a ratio compounded of the sesquiplicate ratio of the radius, and of the subduplicate of that ratio in which the centripetal force of the central body T is diminished or increased by the increase or decrease of the action of the distant body S.
Cor. 7. It also follows from what was before said down, that the axis of the ellipsis described by the body P, or the line of the apsides, does as to its angular motion go forwards and backwards by turns, but more forwards than backwards, and by the excess of its direct motion, is in the whole carried forwards. For the force with which the body P is urged to the body T at the quadratures, where the force MN vanishes, is compounded of the force LM and the centripetal force with which the body T attracts the body P. The first force LM, if the distance PT be increased. is increased in nearly the same proportion with that distance, and the other force decreases in the duplicate ratio of that distance; and therefore the sum of these two forces decrease in a less than the duplicate ratio of the distance PT and therefore by cor. 1. prop. 45. will make the line of the apsides, or, which is the same thing, the upper apsis, to go backward. But at the conjunction and opposition the force with which the body P is urged towards the body T is the difference of the force KL, and of the force with which the body T attracts the body P; and that difference, because the force KL is very nearly increased in the ratio of the distance PT; decrease in more than the duplicate ratio of the distance PT; and therefore by cor. 1. prop. 45. causes the line of the apsides to go forwards. In the places between the syzygies and the quadratures, the motion of the line of the apsides depends upon both these causes conjunctly, to that it either goes forwards or backwards in proportion to the excess of one of these causes above the other. Therefore since the force KL in the syzygies is almost twice as great as the force LM in the quadratures, the excess will be on the side of the force KL, and by consequence the line of the apsides will be carried forwards. The truth of this and the foregoing corollary will be more easily understood by conceiving the system of the two bodies T and P, to be surrounded on every side by several bodies S, S, S, &c. disposed about the orbit ESE. For by the actions of these bodies the action of the body T will be diminished on every side, and decrease in more than a duplicate ratio of the distance.
Cor. 8. But since the progress or regress of the apsides depends upon the decrease of the centripetal force, that is, upon its being in a greater or less ratio than the duplicate ratio of the distance TP, in the passage of the body from the lower apsis to the upper; and upon a like increase in its return to the lower apsis again; and therefore becomes greatest where the proportion of the force at the upper apsis to the force at the lower apsis recedes farthest from the duplicate ratio of the distances inversely; it is plain that when the apsides are in the syzygies, they will, by reason of the subducting force KL or NM - LM, go forward more swiftly; and in the quadratures by the additional force LM go backward more slowly. When the velocity of the progress or slowness of the regress is continued for a long time, this inequality becomes exceeding great.
Cor. 9. If a body is obliged, by a force reciprocally proportional to the square of its distance from any centre, to revolve in an ellipsis round that centre; and afterwards in its descent from the upper apsis to the lower apsis, that force by a perpetual accession of new force is increased more than a duplicate ratio of the diminished distance; it is manifest that the body being impelled always towards the centre by the perpetual accession of this new force, will incline more towards that centre than if it were urged by that force alone which decreases in a duplicate ratio of the diminished distance; and therefore will describe an orbit interior to that elliptical orbit, and at the lower apsis approaching nearer to the centre than before. Therefore the orbit by the accession of this new force will become more eccentrical. If now, while the body is returning from the lower to the upper apsis, it shoulcl describe by the same degrees by which it increased before, the body would return to its first distance; and therefore if the force decreases in a yet greater ratio, the body, being now less attracted than before, will ascent to a still greater distance, and so the eccentricity of the orbit will be increased still more. Therefore if the ratio of the increase and decrease of the centripetal force be augmented each revolution, the eccentricity will be augmented also; and on the contrary, if that ratio decrease it will be diminished. Now therefore in the system of the bodies T, P, S, when the apsides of the orbit PAB are in the quadratures, the ratio of that increase and decrease is least of all, and becomes greatest when the apsides are in the syzygies. If the apsides are placed in the quadratures, the ratio near the apsides is less, and near the sizygies greater, than the duplicate ratio of the distances, and from that greater ratio arises a direct motion of the line of the apsidess as was just now said. But if we consider the ratio of the whole increase or decrease in the progress between the apsides, this is less than the duplicate ratio of the distances. The force in the lower is to the force in the upper apsis, in less than a duplicate ratio of the distance of the upper apsis from the focus of the ellipsis to the distance of the lower apsis from the same focus; and contrary wise, when the apsides are placed in the syzigies the force in the lower apsis is to the force in the upper apsis in a greater than a duplicate ratio of the distances. For the forces LM in the quadratures added to the forces of the body T compose forces in a less ratio, and the forces KL in the syzygies subducted from the forces of the body T leave the forces in a greater ratio. Therefore the ratio of the whole increase and decrease in the passage between the apsides, is least at the quadratures and greatest at the syzygies; and therefore in the passage of the apsides from the quadratures to the syzygies it is continually augmented, and increases the eccentricity of the ellipsis; and in the passage from the syzygies to the quadratures it is perpetually decreasing, and diminishes the eccentricity.
Cor. 10. That we may give an account of the errors as to latitude, let us suppose the plane of the orbit EST to remain immovable; and from the cause of the errors above explained it is manifest, that of the two force NM, ML, which are the only and entire cause of them, the force ML acting always in the plane of the orbit PAB never disturbs the motions as to latitude; and that the force NM, when the nodes are in the syzigies, acting also in the same plane of the orbit, does not at that time affect those motions. But when the nodes are in the quadratures, it disturbs them very much, and attracting the body P perpetually out of the plane of its orbit, it diminishes the inclination of the plane in the passage of the body from the quadratures to the syzygies, and again increases the same in the passage from the syzygies to the quadratures. Hence it comes to pass that when the body is in the syzygies the inclination is then least of all, and returns to the first magnitude nearly, when the body arrives at the next node. But if the nodes are situate at the octants after the quadratures, that is between C and A, D and B, it will appear from what was just now shewn that in the passage of the body P from either node to the ninetieth degree from thence, the inclination of the plane is perpetually diminished; then in the passage through the next 45 degrees. to the next quadrature. the inclination is increased; and afterwards again, in its passage through another 45 degrees to the next node, it is diminished. Therefore the inclination is more diminished than increased, and is therefore always less in the subsequent node than in the preceding one. And by a like reasoning, the inclination is more increased than diminished, when the nodes are in the other octants between A and D, B and C. The inclination therefore is the greatest of all when the nodes are in the syzygies. In their passage from the syzygies to the quadratures the inclination is diminished at each appulse of the body to the nodes; and becomes least of all when the nodes are in the quadratures, and the body in the syzygies; then it increases by the same degrees by which it decreased before; and when the nodes come to the next syzygies returns to its former magnitude.
Cor. 11. Because when the nodes are in the quadratures the body P is perpetually attracted from the plane of its orbit; and because this attraction is made towards S in its passage from the node C through the conjunction A to the node D; and to the contrary part in its passage from the node D through the opposition B to the node C; it is manifest that in its motion from the node C, the body recedes continually from the former plane CD of its orbit till it comes to the next node; and therefore at that node, being now at its greatest distance from the first plane CD, it will pass through the plane of the orbit EST not in D, the other node of that plane, but in a point that lies nearer to the body S, which therefore becomes a new place of the node in antecedentia to its former place. And by a like reasoning, the nodes will continue to recede in their passage from this node to the next. The nodes therefore when situate in the quadratures recede perpetually, and at the syzygies, where no perturbation can be produced in the motion as to latitude, are quiescent; in the intermediate places they partake of both conditions, and recede more slowly; and therefore being always either retrograde or stationary, they will be carried backwards, or in antecedentia, each revolution.
Cor. 12. All the errors described in these corollaries are a little greater at the conjunction of the bodies P, S, than at their opposition; because the generating forces NM and ML are greater.
Cor. 13. And since the causes and proportions of the errors and variations mentioned in these corollaries do not depend upon the magnitude of the body S, it follows that all things before demonstrated will happen, if the magnitude of the body S be imagined so great as that the system of the two bodies P and T may revolve about it. And from this increase of the body S, and the consequent increase of its centripetal force from which the errors of the body P arise, it will follow that all thess errors, at equal distances, will be greater in this case, than in the other where the body S revolves about the system of the bodies P and T.
Cor. 14. But since the forces NM, ML, when the body S is exceedingly distant, are very nearly as the force SK and the ratio of PT to ST conjunctly; that is, if both the distance PT and the absolute force of the body S be given, as ST reciprocally; and since those forces NM, ML are the causes of all the errors and effects treated of in the foregoing corollaries; it is manifest, that all those effects, if the system of bodies T and P continue as before, and only the distance ST and the absolute force of the body S be changed, will be very nearly in a ratio compounded of the direct ratio of the absolute force of the body S, and the triplicate inverse ratio of the distance ST. Hence if the system of bodies T and P revolve about a distant body S; those forces NM, ML and their effects will be (by cor. 2. and 6. prop. 4.) reciprocally in a duplicate ratio of the periodical time. And thence also if the magnitude of the body S be proportional to its absolute force, those forces NM, ML, and their effects, will be directly as the cube of the apparent diameter of the distant body S viewed from T, and so vice versa. For these ratio's are the same as the compounded ratio above-mentioned.
Cor. 15. And because if the orbits ESE and PAB, retaining their figure, proportions and inclination to each other, should alter their magnitude; and the forces of the bodies S and T should either remain, or be changed in any given ratio; these forces (that is, the force of the body T which obliges the body P to deflect from a rectilinear course into the orbit PAB, and the force of the body S, which causes the body P to deviate from that orbit) would act always in the same manner, and in the same proportion; it follows that all the effects will be similar and proportional, and the times of those effects proportional also; that is, that all the linear errors will be as the diameters of the orbits, the angular errors the same as before; and the times of similar linear errors, or equal angular errors as the periodical times of the orbits.
Cor. 16. Therefore if the figures of the orbits and their inclination to each other be given, and the magnitudes, forces, and distances of the bodies be any how changed; we may, from the errors and times of those errors in one case, collect very nearly the errors and times of the errors in any other case. But this may be done more expeditiously by the following method. The forces NM, ML, other things remaining unaltered, are as the radius TP; and their periodical effects (by cor. 2. lem. 10.) are as the forces, and the square of the periodical time of the body P conjunctly. These are the linear errors of the body P; and hence the angular errors as they appear from the centre T (that is the motion of the apsfides and of the nodes, and all the apparent errors as to longitude and latitude) are in each revolution of the body P, as the square of the time of the revolution very nearly. Let these ratio's be compounded with the ratio's in cor. 14. and in any system of bodies T, P, S, where P revolves about T very near to it, and T revolves about S at a great distance, the angular errors of the body P, observed from the centre T, will be in each revolution of the body P as the square of the periodical time of the body P directly, and the square of the periodical time of the body T inversely. And therefore the mean motion of the line of the apsides will be in a given ratio to the mean motion of the nodes; and both those motions will be as the periodical time of the body P directly, and the square of the periodical time of the body T inversely. The increase or diminution of the eccentricity and inclination of the orbit PAB makes no sensible variation in the motions of the apsides and nodes, unless that increase or diminution be very great indeed.
Cor. 17. Since the line LM becomes sometimes greater and sometimes less than the radius PT, let the mean quantity of the force LM be expressed by that radius PT; and then that mean force will be to the mean force SK or SN (which may be also expressed by ST) as the length PT to the length ST. But the mean force SN or ST, by which the body T is retained in the orbit it describes about S, is to the force with which the body P is retained in its orbit about T, in a ratio compounded of the ratio of the radius ST to the radius PT and the duplicate ratio of the periodical time of the body P about T, to the periodical time of the body T about S. And ex æquo, the mean force LM is to the force by which the body P is retained in its orbit about T (or by which the same body P might revolve at the distance PT in the same periodical time about any immovable point T) in the same duplicate ratio of the periodical times. The periodical times therefore being given, together with the distance PT; the mean force LM is also given; and that force being given; there is given also the force MN very nearly, by the analogy of the lines PS, and MN.
Cor. 18. By the same laws by which the body P revolves about the body T, let us suppose many fluid bodies to move round T at equal distances from it; and to be so numerous that they may all become contiguous to each other, so as to form a fluid annulus or ring, of a round figure and concentrical to the body T; and the several parts of this annulus, performing their motions by the same law as the body P, will draw nearer to the body T and move swifter in the conjunction and opposition of themselves and the body S, than in the quadratures. And the nodes of this annulus, or its intersections with the plane of the orbit of the body S, or T, will rest at the syzygies; but out of the syzygies they will be carried backward, or in antecedentia; with the greatest swiftness in the quadratures, and more slowly in other places. The inclination of this annulus also will vary, and its axis will oscillate each revolution, and when the revolution is compleated will return to its former situation, except only that it will be carried round a little by the præcession of the nodes.
Cor. 19. Suppose now the sphærical body T; consisting of some matter not fluid, to be enlarged, and to extend it self on every side as far as that annulus, and that a channel were cut all round it; circumference containing water; and that this sphere revolves uniformly about its own axis in the same periodical time. This water being accelerated and retarded by turns (as in the last corollary) will be swifter at the syzysigies, and slower at the quadratures than the surface of the globe, and so will ebb and flow in its channel after the manner of the Sea. If the attraction of the body S were taken away; the water would acquire no motion of flux and reflux by revolving round the quiescent centre of the globe. The case is the same of a globe moving uniformly forwards in a right line, and in the mean time revolving about its centre. (by cor. 5. of the laws of motion) and of a globe uniformly attracted from its rectilinear course (by cor. 6. of the same laws.) But let the body S come to act upon it, and by its unequable attraction the water will receive this new motion. For there will be a stronger attraction upon that part of the water that is nearest to the body, and a weaker upon that part which is more remote. And the force LM will attract the water downwards at the quadratures, and depress it as far as the syzygies; and the force KL will attract it upwards in the syzygies, and withhold its descent, and make it rise as far as the quadratures; except only in so far as the motion of flux and reflux may be directed by the channel of the water. and be a little retarded by friction.
Cor. 20. If now the annulus becomes hard, and the globe is diminished, the motion of flux and reflux will cease; but the oscillating motion of the inclination and the præcession of the nodes will remain. Let the globe have the same axis with the annulus and perform its revolutions in the same times, and at its surface touch the annulus within, and adhere to it; then, the globe partaking of the motion of the annulus, this whole compages will oscillate, and the nodes will go backward. For the globe, as we shall shew presently, is perfectly indifferent to the receiving of all impressions. The greatest angle of the inclination of the annulus single, is when the nodes are in the syzygies. Thence in the progress of the nodes to the quadratures, it endeavours to diminish its inclination and by that endeavour impresses a motion upon the whole globe. The globe retains this motion impressed, till the annulus by a contrary endeavour destroys that motion and impresses a new motion in a contrary direction. And by this means the greatest motion of the decreasing inclination happens when the nodes are in the quadratures; and the least angle of inclination in the octants after the quadratures; and again, the greatest motion of reclination happens when the nodes are in the syzygies; and the greatest angle of declination in the octants following. And the case is the same of a globe without this annulus, if it be a little higher or a little denser in the æquatorial than in the polar regions. For the excess of that matter in the regions near the equator supplies the place of the annulus. And though we should suppose the centripetal force of this globe to be any how increased so that all its parts were to tend downwards, as the parts of our Earth gravitate to the centre, yet the phænomena of this and the preceding corollary would scarce be altered; except that the places of the greatest and least height of the water will be different. For the water is now no longer sustained and kept in its orbit by its centrifugal force, but by the channel in which it flows. And besides the force LM attracts the water downwards most in the quadratures, and the force KL or NM - LM attracts it upwards most in the syzygies. And these forces conjoined cease to attract the water downwards, and begin to attract it upwards in the octants before the syzygies; and cease to attract the water upwards, and begin to attract the water downwards in the octants after the syzygies. And thence the greatest height of the water may happen about the octants after the syzygies; and the least height about the octants after the quadratures; excepting only so far as the motion of ascent or descent impressed by these forces may by the vis insita of the water continue a little longer, or be stopt a little sooner by impediments in its channel.
Cor. 21. For the same reason that redundant matter in the æquatorial regions of a globe causes the nodes to go backwards, and therefore by the increase of that matter that retrogradation is increased, by the diminution is diminished, and by the removal quite ceases; it follows, that if more than that redundant matter be taken away, that is, if the globe be either more depressed, or of a more rare consistence near the æquator than near the poles, there will arise a motion of the nodes in consequentia.
Cor. 22. And thence from the motion of the nodes is known the constitution of the globe. That is if the globe retains unalterably the same poles; and the motion (of the nodes) be in antecedentia, there is a redundancy of the matter near the equator; but if in consequentia, a deficiency. Suppose an uniform and exactly sphærical globe to be first at rest in a free space; then by some impulse made obliquely upon its superficies to be driven from its place, and to receive a motion, partly circular and partly right forward. Because this globe is perfectly indifferent to all the axes that pass through its centre, nor has a greater propensity to one axis or to one situation of the axis than to any others it is manifest that by its own force it will never change its axis, or the inclination of it. Let now this globe be impelled obliquely by a new impulse in the same part of its superficies as before; and since the effect of an impulse is not at all changed by its coming sooner or later, it is manifest at these two impulses successively impressed will produce the same motion, as if they were impressed at the same time; that is, the same motion as if the globe had been impelled by a simple force compounded of them both (by cor. 2. of the laws) that is a simple motion about an axis of a given inclination. And the case is the same if the second impulse were made upon any other place of the æquator of the first motion; and also if the first impulse were made upon any place in the equator of the motion which would be generated by the second impulse alone; and therefore also when both impulses are made in any places whatsoever; for these impulses will generate the same circular motion, as if they were impressed together and at once in the place of the intersections of the equators of those motions, which would be generated by each of them separately. Therefore a homogeneous and perfect globe will not retain several distinct motions, but will unite all those that are irnpressed on it, and reduce them into one; revolving, as far as in it lies, always with a simple and uniform motion about one single given axis with an inclination perpetually invariable. And the inclination of the axis, or the velocity of the rotation will not be changed by centripetal force. For if the globe be supposed to be divided into two hemispheres, by any plane whatsoever passing through its own centre and the centre to which the force is directed; that force will always urge each hemisphere equally; and therefore will not incline the globe any way as to its motion round its own axis. But let there be added any where between the pole and the æquator a heap of new matter like a mountain, and this by its perpetual endeavour to recede from the centre of its motion, will disturb the motion of the globe, and cause its poles to wander about its superficies, describing circles about themselves and their opposite points; Neither can this enormous evagation of the poles be corrected, unless by placing that mountain either in one of the poles, in which case by cor. 21. the nodes of the æquator will go forwards; or in the equatorial regions, in which case by cor. 20. the nodes will go backward; or lastly by adding on the other side of the axis a new quantity of matter, by which the mountain may be balanced in its motion; and then the nodes will either go forwards or backwards. as the mountain and this newly added matter happen to be nearer to the pole or to the equator.
Proposition LXVII. Theorem XXVII.
The same laws of attraction being supposed, I say that the exterior body S does, by radii drawn to the point O, the common centre of gravity of the interior bodies P and T, describe round that centre areas more proportional to the times, and an orbit more approaching to the form of an ellipsis having its focus in that centre, than it can describe round the innermost and greatest body T by radii drawn to that body.

For the attractions of the bodies S (Pl. 21. Fig. 3.) towards T and P compose its absolute attraction. which is more directed towards O the common centre of gravity of the bodies T and P, than it is to the greatest body T; and which is more in a reciprocal proportion to the square of the distance SO, than it is to the square of the distance ST; as will easily appear by a little consideration.
Proposition LXVIII. Theorem XXVIII.
The same laws of attraction supposed, I say that the exterior body S will, by radii drawn to O the common centre of gravity of the interior bodies P and T, descbribe round that centre, area's more proportional to the times, and an orbit more approaching to the form of an ellipsis having its focus in that centre, if the innermost and greatest body be agitated by these attractions as well as the rest, than it would do if that body were either at rest are not attracted, or were much more or much less attracted or much lire or much less agitated.
This may be demostrated after the same mamner
as prop. 66. but by a more prolix reasoning,
which I therefore pass over. It will be sufficient
to consider it after this manner. From the demonstration
of the last proposition it is plain, that
the centre, towards which the body S is urged by
the two forces conjunctly, is very near to the common
centre of gravity of those two other bodies.
If this centre were to coincide with that common
centre, and moreover the common centre of gravity
of all the three bodies were at rest; the body
S on one side, and the common centre of gravity
of the other two bodies on the other side.
would describe true ellipses about that quiescent
common centre. This appears from cor. 2. prop.
58. compared with what was demonstrated in
prop. 64 and 65. Now this accurate elliptical
motion will be distributed a little by the distance
of the centre of the two bodies from the centre
towards which the third body S is attracted. Let
there be added moreover a motion to the common
centre of the three, and the perturbation will be
increased yet more. Therefore the perturbation is
least when the common centre of the three bodies
is at rest; that is, when the innermost and
greatest body T is attracted according to the same
law as the rest are; and is always greatest, when
the common centre of the three, by the diminution
of the motion of the body T; begins to be
moved, and is more and more agitated.
Cor. And hence if more lesser bodies revolve about the great one, it may easily be inferred that the orbits described will approach nearer to ellipses, and the descriptions of area's will be more nearly equable, if all the bodies mutually attract and agitate each other with accelerative forces that are as their absolute forces directly, and the squares of the distances inversely; and if the focus of each orbit be placed in the common centre of gravity of all the interior bodies; (that is, if the focus of gravity and innermost orbit be placed in the centre of gravity of the greatest and innermost body; the focus of the second orbit in the common centre of gravity of the two innermost bodies; the focus of the third orbit in the common centre of gravity of the three innermost; and so on) than if the innermost body were at rest, and was made the common focus of all the orbits.
Proposition LXIX. Theorem XXIX.
In a system of several bodies A, B, C, D, &c. if any one of thos bodies or A, attract all the rest, B, C, D, &c. with accelerative forces that are reciprocally as the squares of the distances from the attracting body; the absolute forces of the attractive bodies A and B will be to each other, as those very bodies A and B to which these forces belong.
For the accelerative attractions of all the bodies B, C, D, towards A are by the supposition equal to each other at equal distances; and in like manner the accelerative attractions of all the bodies towards B are also equal to each other at equal distances. But the absolute attractive force of the body A is to the absolute attractive force of the body B, as the accelerative attraction of all the bodies towards A to the accelerative attraction of all the bodies towards B at equal distances and so is also the accelerative attraction of the body B towards A, to the accelerative attraction of the body A towards B. But the accelerative attraction of the body B towards A is to the accelerative attraction of the body A towards B as the mass of the body A to the mass of the body B; because the motive forces which (by the 2d, 7th, and 8th definition) are as the accelerative forces and the bodies attracted conjunctly, are here equal to one another by the third law. Therefore the absolute attractive force of the body A is to the absolute attractive force of the body B as the mass of the body A to the mass of the body B. Q. E. D.
Cor. Therefore if each of the bodies of the
system A, B, C, D, &c. does singly attract all the
rest with accelerative forces that are reciprocally as
the squares of the distances from the attracting
body; the absolute forces of all those bodies will
be to each other as the bodies themselves.
Cor. 2. By a like reasoning if each of the bodies of the system A, B, C, D, &c. do singly attract all the rest with accelerative forces, which are either reciprocally or directly in the ratio of any power whatever of the distances from the attracting body; or which are defined by the disŧances from each of the attracting bodies according to any common law; it is plain that the absolute forces of those bodies are as the bodies themselves.
Cor. 3. In a system of bodies whose forces decrease in the duplicate ratio of the distances, if the lesser revolve about one very great one in ellipses, having their common focus in the centre of that great body, and of a figure exceeding accurate; and moreover by radiu drawn to that great body describe area's proportional to the times exactly; the absolute forces of those bodies to each other will be either accurately or very nearly in the ratio of the bodies. And so on the contrary. This appears from cor. of prop. 68. compared with the first corollary of this prop.
Scholium.
These propositions naturally lead us to the analogy there is between centripetal forces, and the central bodies to which those forces use to be directed. For it is reasonable to suppose that forces which are directed to bodies should depend upon the nature and quantity of those bodies, as we see they do in magnetical experiments. And when such cases occur, we are to compute the attractions of the bodies by aligning to each of their particles its proper force, and then collecting the sum of them all. I here use the word attraction in general for any endeavour, of what kind soever, made by bodies to approach to each other; whether that endeavour arise from the action of the bodies themselves as tending mutually to, or agitating each other by spirits emitted; or whether it arises from the action of the æther or of the air, or of any medium whatsoever, whether corporeal or incorporeal, any how impelling bodies placed therein towards each other. In the same general sense I use the word impulse, not defining in this treatise the species or physical qualities of forces, but investigating the quantities and mathematical proportions of them; as I observtd before in the definitions. In mathematics we are to investigate the quantities of forces with their proportions consequent upon any conditions supposed; then when we enter upon physics, we compare those proportions with the phænomena of Nature; that we may know what conditions of those forces answer to the several kinds of attractive bodies. And this preparation being made, we argue more safely concerning the physical species, causes, and proportions of the forces. Let us see then with what forces sphærical bodies consisting of particles endued with attractive powers in the manner above spoken of must act mutually upon one another; and what kind of motions will follow from thence.