The Solar System/Chapter 1
THE SOLAR SYSTEM
I
OUR SOLAR SYSTEM
In the long perspective of knowledge, whichIts position in space and in knowledge. begins with the close at hand and stretches to the infinitely remote, the solar system marks a middle distance. Between the intimacy possible with objects on this Earth and the distant recognition of the universe of suns, it furnishes an acquaintanceship combining something of the interest of the one with the grandeur of the other.
Our knowledge about the solar system hasIts constituents. greatly increased during the last quarter of a century; and first in the recognition of what makes part of it. To our solar system we now know belongs every heavenly body we see except the fixed stars and the nebulæ. Not only are the Sun, Moon, and planets members of it, but meteors, shooting-stars, and comets we have found to be so, too. That all of these bodies are part and parcel of what the Sun controls, I shall first proceed to show you; for it is proper that we should recognize the members of the system before considering the system's constitution and the several characters of its constituents.
In many text-books you shall find it still statedObsolete views. that these flaming portents, the cometæ or long-haired stars,—for the ancients saw tresses where we prosaically see tails,—one of which, on the average, startles a generation into wonder, are visitors to us from other stars. So also we were taught that the strange stones that fall to us from the sky, and we call meteorites, were bits of some body from far interstellar space. Such knowledge belongs now to the history of science, not to science itself; for these bodies carry with them their badge of membership: it shows in the orbits they describe. So, when we pass through a comet's tail, or pick up a piece of meteoric iron, we now recognize that we have to do, not with a stranger, but with our own kith and kin. Man may gaze at matter beyond the solar system, but man has never yet touched it.
Proof of community lies in the character of the paths.Path the proof of oneness. Planet and particle alike turn out to travel in ellipses, and ellipticity betrays association. How the orbit labels the occupant we shall see, on finding the paths the planets pursue and why they pursue them. The orbits of the planets are then the first point to consider.
To begin with the Sun. Observation shows notEarth travels in an ellipse. only that the Sun changes its place in the heavens, but changes its size as well. To measurement through a smoked glass, it seems to contract in summer and expand in winter. Plotting the directions it successively takes in the form of a spider, and taking the legs inversely proportionate to the diameters at the times, we find an ellipse, in one of whose foci lies the Sun. The Earth, then, goes round the Sun in an ellipse.
To find the path of a planet, we first get itsSo do the other planets. synodic period, or period with regard to the Sun. Then, from a sufficient number of observations of synodic periods to give their mean, we obtain the sidereal period, or period with reference to the stars.
By considering the angular motions, the two periods are easily seen to be connected by the following equation:—
Where E = the Earth's period; S = the Planet's synodic period; P = the Planet's sidereal period.
From two bearings separated by a sidereal period, we get a quadrilateral, of which, knowing parts enough to solve, we derive the planet's distance from the Sun at the moment. We now
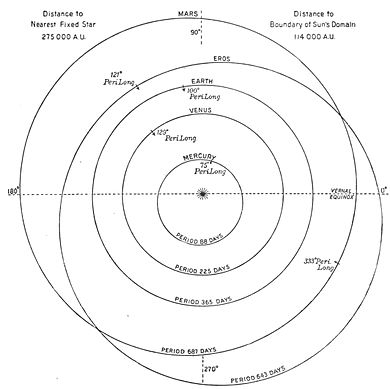
Fig. I. Inner Planets.
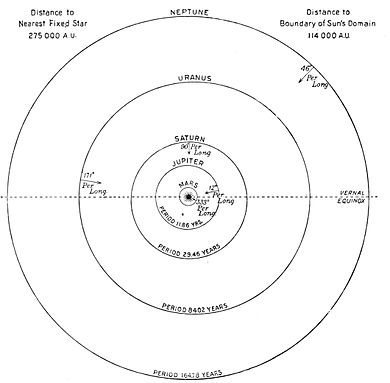
Fig. II. Outer Planets.
have for the planet what we had for the Sun,—direction and distance at a given time. Dotting these data upon the apparent path, Kepler proved that the orbit of Mars was an ellipse. Mars was the first of the planets thus to have its orbit found; following it the others yielded similarly to the genius of the man. All the planets, then, move in ellipses about the Sun.
Thus we have obtained the accompanying plan of the system.
Kepler discovered two more relations: first,Kepler's laws. that the radius vector of any planet swept over equal areas in equal times; and, second, that the cubes of the major axes of the orbits of any two planets were as the squares of their periodic times. The latter is not exactly true, but becomes so if we take the masses at work into account.
From these three "laws," Newton showed that the force governing the motions of the planets was in each case directed to the Sun, and was as the inverse square of the distance from him. Reversely he showed that such being the law of gravitation, the orbits must all be conic sections.
But conic sections are of two kinds,—ellipses Ellipses and hyperbolas. or closed curves, and hyperbolas or curves that do not return into themselves. Clearly permanent members of a system must travel in the first of these two classes of curves, visitors only in the second. Here, then, we have an instant criterion for distinguishing bodies that belong to our system from those that visit it from without.
Which of the two orbits a body is pursuing may be determined either by actually finding the body's path or by finding the distance of the body from the Sun and its speed at the moment. For an interesting equation connects the speed with the distance, giving the major axis of the orbit, upon which alone the class of curve depends. This equation is
Suppose a body at p moving along the curve whose tangent is pt with acceleration f always directed to s. Then , the resolved part of the acceleration along the tangent, is f cos ψ.
The resolved part of the velocity v along sp is , and
c can be determined from the actual velocity at some point in the orbit (at the end of the minor axis, for instance, in the ellipse), and from this we can find that
The velocity in the hyperbola thus exceeds that in the ellipse, and the dividing line between the two classes of curves is clearly when the second term is zero.
Consequently
Now the planets all move in ellipses. They are therefore under the Sun's control and form part of his system.
Occasionally stones fall out of the sky on toMeteors. the earth. Suddenly a flash occurs overhead, a detonation follows, and then if the observer be near enough, a mass of stone or iron is seen to bury itself in the ground. This is a meteorite, aerolite, or bolide, a far wanderer come at last to rest.
The flash, the report, and the fused exterior of the mass found are due to the meteor's striking against our air. The bodies enter the upper atmosphere at speeds of from ten to forty miles a second, and such speeds are equivalent to immersing them in a blow-pipe flame of a temperature of many thousands of degrees. For the temperature of a gas is as the mean velocity-square of its molecules, and the rush of the meteor produces the same effect as if the molecules of the air were moving and the air therefore very hot.
Its outward condition is a consequence of thePreviously cold. last stage in its journey, but its inner state at times continues to bear witness to a previous condition. If the mass be large, time does not suffice to fuse more than its exterior, and the interior retains the cold of interplanetary space. As Young tells us, one of the fragments of the Dhurmsala meteorite in India was found in moist earth, half an hour or so after its fall, coated with ice!
But their speed is the real tell-tale upon theirTheir orbits short ellipses. past. An ingenious investigation by the late Professor Newton, whose specialty was these very things, proved that ninety per cent., and probably all of the meteorites for which we have sufficient data, were traveling, before their encounter with the earth, in orbits not parabolic, but elliptic, like those of the short-period comets, and were moving direct. They come to us, therefore, not from the stars, but from the Sun's own domain. They, too, then are members of the system.
Most interesting is their constitution in itsTheir origin. bearing upon their origin. Some are stone, some iron—meteoric iron joined with nickel. Now the iron meteorites are saturated with occluded gases, which can be extracted from them by suitable processes, and which cannot have been occluded originally except in the molten interior of a sun, intense heat and excessive pressure being necessary; and as they are now ungathered in remnants of our own once nebulous mass, they must betray what that nebulous mass was to begin with; for in their subsequent history there has been nothing to make them what they are. They cannot have come from our present sun, since it became a sun, as their orbits conclusively show. They must have come from the sun our system had before the catastrophe, which caused the nebula which caused our Sun, occurred. They antedate the creation of the nebula itself which our nebular hypothesis posits as the beginning of things. They are old with an age which staggers imagination; older in cycles of evolution, if not in years, than anything we see in the countless spangles of a winter's night in the blue-black firmament of sky. Before the silent tale they tell, history shrinks into yesterday, the Earth's career into the day before, and the evolving of the solar system itself into modernity. Through that strange Widmannstättian fretwork that marks their surface like the lacing of frost-work on a window-pane, we seem to be gazing past the iron bars into the immensity, not of space alone, but of eternity.
Next to meteors, and doubtless close to themShooting-stars. in kind, come shooting-stars. Superficial distinctions have caused them to be classed apart, but in all likelihood size alone separates the two.
In the case of shooting-stars, we have the flash, the lingering scarf of light left when the body itself has eluded us, but no sound is heard, and nothing reaches the earth.
The visitants come, too, in swarms. They haveMeteor-streams. their times and seasons. Different nights of the year are consecrate to special flights; and the successive years bring back the same flights like birds that honk overhead at the same recurrent season of the year.
Such regularity has caused them to be noted and studied, and we have now a score of well-recognized congeries of shooting-stars or meteoric streams, known, for example, as the Leonids, the Perseids, the Andromedes. Each swarm has its radiant or perspective point from which all its members seem to come. From this radiant it derives its name, the Leonids seeming to come from a point in the constellation Leo, the Orionids from the constellation of Orion, and the Lyrids from the Lyre.
Each of these swarms enters our atmosphereTheir speeds. with cosmic speed, all the shooting-stars of one swarm travelling at the same rate; but each swarm has its own distinctive velocity. The Andromedes move relatively slowly,—eleven miles a second,—and are reddish. They overtake us; this accounts for their sluggishness, and their sluggishness explains their color. They are only red-hot. The Perseids move with medium velocity. They strike us on the quarter at twenty-five miles a second, and they are yellow. The Leonids, or November meteors par excellence, meet us head on at forty-three miles an hour, their swiftness giving them a bluish-green tint or a white heat.
To Professor Newton again we owe our firstTheir orbits elliptic. step to knowledge of them. After the shower of the Leonids in 1866, he determined, from all the observations upon them, five orbits which they might have pursued; and then Adams, of Neptunian fame, from the motion of their node, showed that only one of the five, an orbit with a period of thirty-three years, would satisfy the problem. Thus was explained the similar shower of 1833 and the yet earlier one of 1799, seen by Humboldt. We should have had them again in 1900, but that Jupiter probably interfered.
In the same way, the Andromedes prove to travel in an orbit whose period is thirteen years, and whose aphelion lies just outside the orbit of Jupiter. So, also, the Perseids pursue a closed orbit, but a much larger one, which takes them far beyond the orbit of Neptune.
Shortly after Newton and Adams had worked out the path of the November meteors, Schiaparelli attacked the orbit of the Perseids, or AugustAssociation of meteor-streams with comets. meteors, and to the astonishment of the scientific world brought out the surprising fact that they

Fig. III. Meteor Streams.
travelled in an orbit substantially coincident with that of the great comet of 1862, known as Tuttle's comet (1862 III.). About the same time, Leverrier published his orbit of the Leonids, and nearly simultaneously Oppolzer, the great comet computer, published his of Tempel's comet of 1866 (1866 I.), and the two were found to be practically identical. Here were two identities which could hardly be the result of chance. Researches since have added to the number of such comet-meteor associations. Professor Herschel catalogues seventy-six; and four pairs—the Leonids and Tempel's comet, the Perseids and Tuttle's comet, the Andromedes and Biela's comet, and the Lyrids and the comet of 1861 (1861 I.)—are shown in the diagram on the opposite page.
Thus are comets and meteors connected. ButComets become meteor-streams. we know more about their connection than this simple fact of association. We know that the one becomes the other, for we have seen the process of transformation take place practically under our very eyes. Biela's comet was for many returns a well-ordered member of Jupiter's comet-family, of which family we shall have more to say in the fifth chapter. Up to 1839 it had returned with due regularity and without incident. In 1846, it again appeared on time, but thereupon proceeded to do something very strange and then unheard-of. In mid-career it split. It was first seen on November 28, and presented the appearance of the usual comet. By December 19 it had become pear-shaped, and on January 13 it divided, the two halves at first separating, and thenceforth travelling side by side at a distance of one hundred and sixty thousand miles for the subsequent four months during which they continued visible. A bridge of light sometimes spanned the interval between them.
In 1852 the two returned. The distance between the pair had now increased to one million five hundred thousand miles, and they travelled thus during the time of their visibility.
Neither has ever been seen since; but in 1872, just when the Earth was passing the track of the lost heavenly twins, on November 27, occurred a brilliant star-shower. The German astronomer, Klinkerfues, was so impressed with the belief that this must be the remains of the comet, and that the comet itself, or what was left of it, would be seen exactly opposite the radiant, that he telegraphed at once to Pogson, the government astronomer at Madras, India: "Biela touched Earth November 27; search near Theta Centauri." Pogson looked. Clouds at first prevented, but on the third morning it was fair, and he saw in the predicted place a comet with a round head and a faint tail moving as it should have done. The next morning he observed it still better, and in its proper place. Oppolzer, by assuming the major axis, showed that this may have been Biela's comet.
Since then, other comets have been observed to split up, due to the action of the planets near which they chance to pass; and Callandreau has shown that the event ought not to be so very uncommon.
Another point connected with these meteorMeteor streams attendant upon planets . streams must be noticed. Each of them is associated with the orbit of some particular planet. The planet in some sense shares with the Sun a control over the stream. It cannot cause the stream to circle round itself, but it can, and does, cause it to pay periodic obeisance to its might. The stream's perihelion remains at the Sun, but its aphelion becomes its periplaneta. It sweeps about the planet at the one end of its path somewhat as it sweeps round the Sun at the other.
The Andromedes are thus dependent on Jupiter, the Leonids on Uranus; while the Perseids and the Lyrids go out to meet the unknown planet which circles at a distance of about forty-five astronomical units from the Sun.
It may seem to you strange to speak thus confidently of what no mortal eye has seen, but the finger of the sign-board of phenomena points so clearly as to justify the definite article. The eye of analysis has already suspected the invisible.
In our identification of the members of ourConspicuous comets. system we have thus got steadily farther and farther away. We began with the planets. Then we attacked the less evident and more erratic bodies, and we found that the nearest of them, the meteorites, were after all fellow-members, and circled quite near us, their orbits being comparable with, and possibly not alien to, the short-period comets.
Next we found the shooting-stars, the meteor streams, to be sun-controlled but travelling farther yet out into space, and connected with comets known to be periodic. We have now to take another step outward to the comets non-periodic, among which the most conspicuous of those visitants are numbered.
Non-periodic we may call them pending investigation. For their orbits are so vast that we know but vaguely what their major axes are.
Some four hundred of these stars with tressesParabolic comets. have been seen from the earliest times of which we have records to the present day. Not a year passes that several are not discovered, but conspicuous ones are not over-common. In the last forty years there has been but one of superlative mien, and that was twenty years ago. The present generation has no conception of what a comet worthy the name can be. One of my first recollections 
Fig. IV. Conspicuous Comets.
From this fact of a practical parabolicity ofTheir orbits. path many astronomers have argued the exterritoriality of these bodies, and early in the last century Laplace set himself the problem of finding the probability of hyperbolic to elliptic orbits on the theory that they all came to the Sun from stellar space. In spite of several mistakes in his work, first pointed out by Gauss, he reached a conclusion which is correct in quality: that the number of hyperbolic orbits to elliptic should be very small, less than one in the whole number already seen, on the tacit assumption that the Sun was at rest.
But the Sun is not at rest. It is traveling atConclusion as to connection with the solar system. the rate of eleven miles a second towards a point in the constellation Hercules, carrying its retinue with it; and this motion quite alters the result. Instead of a great preponderance of elliptic orbits, the solution shows in this case a large excess of hyperbolic ones. And in most of the orbits the hyperbolicity would be marked, not faint and doubtful. To Schiaparelli we owe the first suggestion of this fact, and, in 1895, to Fabry, of the observatory of Marseilles, a very elegant and conclusive memoir on the subject.[1]
In view of this we see that comets behave not as they would, did they come to us as visitors from other stars, but just as they should, considered as distant members of our own system. Comets, then, are also all co-members of the system.
That there is quite room enough within theThe Sun's domain. Sun's paramount domain for their gigantic orbits becomes evident when we consider the distance to which that domain extends. Measured even on the vast scale of our solar system, the gap which sunders it from the nearest fixed star is something enormous. Two hundred and seventy-five thousand times our distance from the sun is the space that divides us from the next sun, the star α Centauri. This distance is found by noting the shift in the star's position due to the extreme swing of the Earth in her orbit called the annual parallax. It is a very minute displacement at most, and requires perhaps the most delicate of all astronomical refinement to detect. Incidentally it affords conclusive evidence of itself that the Earth goes round the Sun, not the Sun round the Earth.
Fortunately α Centauri, our nearest stellarα Centauri. neighbour, is a double star, a binary system, and thus of itself affords us information of the region over which it exercises control. Assuming that gravity acts there just as it does here,—any other possible assumption implies that the force depends on the orientation, which does not seem rational,[2]—we can deduce from the motion of the pair their united mass. It comes out twice that of our Sun. Now, as gravity is as , we have, calling the whole distance from us to them a, the following quadratic to give us d, the boundary distance between the two domains, our Sun's and α Centauri's,
Neptune, the farthest known planet at present, is but thirty astronomical units away, or about only of the distance to the limit of the Sun's domain. How nestled we all are under the Sun's protecting wing is evident. It is no wonder that the remotest comets seem almost infinitely distant at their aphelion, though part and parcel of the brood.
Coming back now from these chill outerThe several planets. confines of the Sun's territory to the inner family circle gathered about the hearth or focus of all these ellipses, occupied by the Sun,—for such is the literal meaning of the word "focus,"—we must note how the main bodies and yet smaller particles are severally ranged about it.
Humboldt divided the planets into two groups :Terrestrial and major planets. the terrestrial planets and the major planets, and this classification one shall still find in many a text-book. But it has long since ceased to contain even a specious distinction. The so-called terrestrial planets differ among themselves quite as much as any of them do from the major planets. From our present knowledge it would be much nearer the mark to divide the eight into pairs, Mercury and Venus, the Earth and Mars, Jupiter and Saturn, Uranus and Neptune ; yet even between the members of each pair are notable differences, to say nothing of the asteroids which throng the space betwixt Jupiter and Mars.
Of the differences, it will be the province of the succeeding chapters to speak ; but before doing so, let us take a bird's-eye view of the whole.
Our own Solar System has one characteristic,Solar System a single-star one. a general family trait, which distinguishes it from many that lie round about it in space ; for we may not doubt that the stars are centres to systems of their own. We have not only analogy to guide us to this deduction, but we already have glints of evidence of the fact. Our system differs, how ever, from many of its neighbours in being a single-sun system. This is a very important and fundamental distinction. To begin with, it makes cosmic principles much easier to understand. We think celestial mechanics abstruse enough as they are, but ours are child's play to the complications which two suns, to say naught of three or four, would introduce into any system over which they jointly held sway. It is problems of this nature which Professor Darwin and other modern analysts are trying to unravel. Difficult as the conceptions are, it is a question whether life itself would not be quite as difficult, under such conditions. Take our nearest stellar neighbour, α Centauri, for instance, and consider what a planet circling round either or both of its suns would be called upon to undergo. Certainly our orderly succession of phenomena would be seriously disturbed to the consequent inconsequency of development upon its surface. Day and night would become meaningless terms, and organisms would have to put up with variations which make imagination stare.
For fashioning worlds like the terrestrial, a single-star system is, in general, a prerequisite.
This oneness is due to the system's originalDue to small initial moment of momentum. small moment of momentum. A minimum moment of momentum is caused by the centralization of the mass; a maximum by its equal division into two or more. If we calculate the moment of momentum of the Solar System to-day, and compare it with that of any binary system, we shall find it in comparison almost vanishingly small.
The system, 61 Cygni, with only one fifth of its mass, has a moment of momentum two hundred and fifty times as great, and that of α Centauri, which has twice the mass, has two thousand times the moment.
This means that in the region of space, which made room to the solar nebula, the individual motions must have been either small or equally large in all directions, the negative motions almost exactly cancelling out with the positive ones.
- ↑ Annales de la Faculté des Sciences de Marseille.
- ↑ Binaries move in apparent ellipses. Parallel projection keeps an ellipse an ellipse and the centre the centre. From the general polar equation of a conic and the differential equation of the orbit,
,it appears that the only laws of force which do not depend on θ, that is, on the orientation, are , which is negatived by the fact that no star has yet been found in the centre of the apparent ellipse, and , which is thus the only law possible which is rational. It is thus ably put by Moulton (Celestial Mechanics, 1902).















