The Solar System/Chapter 5

by Percival Lowell

V
JUPITER AND HIS COMETS

Jupiter exemplifies choas.Chaos describes Jupiter at present; the seething something between sun and world. The planet is either a sun in its senility or an earth in its babyhood, as you are pleased to regard it. For the one state passes by process of development into the other.

A semi-sun.Viewed as a sun, it lacks little except light; viewed as a world, it wants everything except that lack of luminosity. It is, as Virgil described another giant, informe ingens cui lumen ademptum. Its density is almost exactly that of the Sun itself. Either, therefore, its bulk is chiefly atmosphere round a kernel of planet, which is Professor Darwin's conclusion, or its smaller mass is offset by its lesser heat, causing a like condensation of the two globes. On the latter supposition, though not luminous, it is still hot. This would bear out and confirm the inference, from the brick-red color between its belts, that its surface is at a red heat.

Almost precisely the same is true of Saturn; the body of that planet, too, being a faint cherry red. Jupiter, however, we see much the better of the two, and we may describe it as typifying both.

Both are bulky; their masses to their volumes being such that their mean densities are respectively somewhat greater (1.28%) and somewhat less than water (.69%). Both are in rapid rotation; particles on their equators traveling with speeds comparable with their orbital velocities. Both, in consequence, are strikingly flattened into oblate spheroids whose elliptic curves instantly strike the eye. In the disks of both we look only upon atmosphere and cloud. Lack of solidity, speed of self-movement, cloudy condition, are all so many signs of—youth. In relative—if not in absolute—age, both planets are still very young.

Semi-suns in several senses, the two planets are three-quarters way in their journey from nebula to world. In their traits both more closely resemble the Sun than the Earth. Indeed, with the trifling exception of not shining, the disk of Jupiter or of Saturn bears a very remarkable analogy to the solar.

Ruddy glow.In a large telescope and in good seeing, Jupiter is a color-picture as beautiful as it is marked. A deep pink flush suffuses the planet's equatorial regions. It probably betokens the parts of the true surface that are laid bare. For that the color is due to the selective absorption of the higher regions of the planet's air is negatived by the spectroscope, which shows dark bands in the red.

Rotation.In spite of its enormous bulk, Jupiter turns on its axis with such speed that its figure is flattened by $\scriptstyle {\frac {1}{15.5}}$. Its mean time of rotation is 9^h 55^m. We are forced to say its mean time, not because the markings cannot be accurately timed, nor because of any change in the planet's moment of momentum, but because the planet does not rotate as a whole. Different parts of it go round at different rates. Speaking broadly, the nearer the equator the greater the speed. Between the equator and latitude 30° there is a difference of six minutes in the rotation period. But the several belts have each its own period, and this does not always accord with the latitude. In addition, particular spots on the same longitude have particular spins, and pass by each other at speeds from seven miles to four hundred miles an hour. White markings travel faster than dark markings close beside them. Thus the white masses around the great red spot drift by it. The spot itself has changed its rate by six seconds in as many years. It is pretty evident that Jupiter is chaotic.

Rotation of Saturn.The same is the case with Saturn. Stanley Williams, in 1893, found for the Saturnian regions between 6° N. and 2° S., 10^h13^m, and for those between 17° N. and 27° N., 10^h15^m. Not only did latitudes differ in rate, but different longitudes went each at its own pace.

Sun's rotation.Something similar is true of the Sun. At the Sun's solar equator the spin is swifter than on either side of it; and the rate decreases steadily from the equator towards the poles. Spots near the equator go round in 25 days (25.23 days), spots in latitude 30° in 26½ days, in latitude 40°, 27 days, while in latitude 45° they take fully two days longer than in 0°. Now Willsing and Professor Sampson, of Durham University, have shown that such a state of things should result in the process of condensing from nebula to star. In the nebula, if the density varied from place to place, which, on the doctrine of chances, would certainly be the case, the several parts would revolve round their common centre of gravity at various rates. As the nebula condensed, such parts as held together would tend to equalize their individual motions through friction, until a common rotation was brought about. But this would consume a long time; in the mean while, the equatorial parts would outstrip the others. In the midst of the equalizing process the Sun, Jupiter, and Saturn now seem to be.

Jupiter has cloud layers.Jupiter, however, has progressed beyond the Sun in that the outer layers of his substance have cooled down enough to condense into cloud, due, possibly, to the planet's smaller mass. On the surface of the Sun things are still kept largely uniform by the terrific heat, and the slower rotation lets us perceive no latitudinal layers. On the contrary, Jupiter's disk is striated with belts of various tone and tint, according almost exactly to the parallels; while the albedo, or relative brightness of the disk, 62 per cent, of absolute whiteness, indicates that most of it is cloud.

Jupiter's clouds self-raised not Sun-raised.These clouds are quite unlike our terrestrial ones. Jupiter's clouds are not Sun-raised, but self-raised condensations. On the one hand, the Sun's action there, only $\scriptstyle {\frac {1}{27}}$ of what it is here, is impotent to produce the effect we see; on the other, the cloud zones show a persistence quite disregardant of the Sun. They are not ephemeral like ours, but long-lived, lasting for weeks, months, and even years. They must, therefore, be Jove-caused.

Disk darkens toward limb.In another feature Jupiter resembles the Sun. Its disk darkens to the limb. None of the smaller planets do this. The only thing capable of producing such effect is a layer of atmosphere surrounding the disk of considerable depth. Jupiter's atmosphere is dense, and the absorption to which a ray of light would be subjected in passing in from the Sun and then out to us would increase from centre to circumference, and thus dim the edges of the disk.

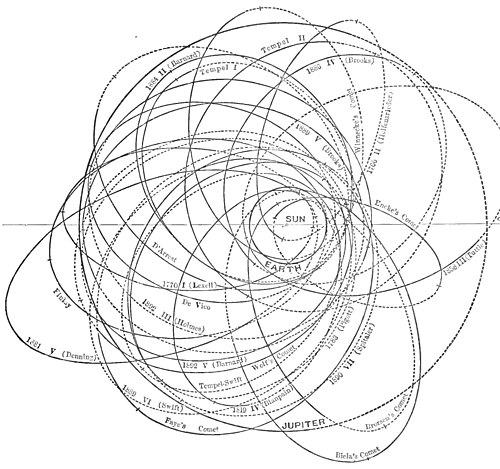
Comets associated with Jupiter.Jupiter has two families of bodies connected with him; one an own one of satellites, the other with an adopted one of comets. With his satellites we made acquaintance in the last chapter; we must now be introduced to his comets.

Thirty-two comets circle near the planet and agree in the following distinguishing characteristics:—

1. Their aphelia hug Jupiter's orbit.

2. Their ascending nodes occur close to it.

3. Their motion is direct.

Association suggests capture.At some time in the past, therefore, each of these comets must have passed close to Jupiter, the comet and the planet chancing to arrive together at the node. At that epoch the comet must have suffered great disturbance at the hands of the planet, and its previous orbit have been radically changed.

D'Alembert, accordingly, suggested that Jupiter had captured these comets, and Laplace

FIG. XIII. JUPITER'S FAMILY OF COMETS.

extended the idea; but to Professor H. A. Newton we owe the most important research in the matter. In two striking memoirs (1878 and 1893), he showed that Jupiter was quite capable of such capture; but he started with the assumption that comets were not denizens of the Sun's domain, so he considered only parabolic comets.

Comets all belong to the solar system We now know that all comets probably that man has ever seen are part and parcel of the Sun's retinue. They do not come to us from outer space, but are stable, if erratic, members of the solar system. In the light of this fact, we may profitably reconsider the subject.

Jupiter's sphere of influence. Picture a comet, coming in to the Sun from space, to pass close to the planet in its journey, Within a certain distance of Jupiter, the planet's pull becomes so great that it is mechanically more exact to regard the comet as obeying Jupiter and perturbed by the Sun; and if the approach be very close, we may neglect in a first approximation the Sun's effect during the passage. This region is called Jupiter's sphere of influence, and is of the general shape of an ellipsoid, whose longest diameter follows the planet's path. The mean radius of the ellipsoid is three tenths of the Earth's orbit, no inconsiderable distance, and the extreme radii differ as 1 to 1.19.

Relative orbit about a planet an hyperbolaAs the comet is traveling, when it enters the planet's sphere or influence, with Sun-imposed velocity, its speed, even if the orbit be elliptic of small major axis, will exceed what Jupiter could cause. It will, in general, approach Jupiter with Jovian hyperbolic velocity, and its relative orbit about the planet will be an hyperbola. Jupiter, therefore, cannot completely possess itself of the comet.

Comet accelerated or retarded according as it passes behind.The general equation of the relative motion I shall not bother you with. But certain deductions from it I think you will find of interest. In the first place, it appears that the comet will be accelerated or retarded, according as it passes behind or in front of the planet. This may be seen directly from the consideration that if it pass in front of the planet, it accelerates the latter, and since action and reaction are equal and opposite, it must itself be retarded; contrariwise, if it pass behind the planet.

Parabola made into ellipse by retardation.Suppose now the comet to have been pursuing a parabolic path before the encounter; then the least retardation will make of its orbit an ellipse; for whether a body move in an ellipse, a parabola, or an hyperbola is a question simply of its speed at a given distance, shown by the well-known equation,—

$\textstyle v^{2}=\mu ({\frac {2}{r}}-{\frac {1}{a}}).$

Into hyperbola by acceleration.Similarly, the least acceleration will throw it into an hyperbola, and it will pass out of the solar system, never to return.

For an original elliptic orbit, this is not necessarily the case. A comet pursuing such a path may have its velocity increased and yet not pass out of the system. In many cases, however, it would so result, and we can thus perceive how comets might come to us from other systems from purely internal forces there.

Jupiter's maximum effect in shortening comet's major axis The maximum effect in retarding the comet's motion occurs when the comet approaches Jupiter in such a direction and with such a relative speed as to be turned back upon the planet's path, and to leave the planet in the direction of the planet's quit, with a relative speed equaling the planet's own. It is then left stock-still to fall into the Sun.

Jupiter's absolute maximum effect Jupiter can do more than this. Though to leave a comet stock-still to drop into the Sun, thus shortening the major axis to one half its own, is its maximum effect in the way of contracting the orbit, its power over the comet exceeds such limit. The planet can actually prevent a comet bound round the Sun from attaining its object. It can cause the comet to make itself in place of the Sun the goal of its pilgrimage, and sweeping round the planet, to go back into space without visiting the Sun at all.

Consider the hyperbola the planet causes the comet to describe. What the planet does is to

Jupiter's bulk limits his power.swing the incoming asymptote of this hyperbola through a certain angle. Clearly, the closer the perijove of the relative orbit, the greater this angle

The comet's direction may be turned from OA to OB; or OA′ to OB′; or OA″ to OB″,according as it approaches along OA, OA′ or OA″, P being the planet.

FIG. XIV. RELATIVE ORBITS.

of swing, as the planet gets a greater pull upon the particle. If the comet were not coming too fast and Jupiter's own body did not get in the way, the comet could be turned straight back whence it came. Practically, Jupiter's bulk does get in its way, and the limit of the planet's power lies below such direct reversal; nevertheless, it is sufficient in many positions to cause the comet to sweep round and dart away from the Sun with a speed such as to carry it beyond the Sun's control.

The planet's greatest effect in turning the comet is shown in three different conditions of approach. The comet enters along the unbroken lines and leaves by the broken ones.

Deflective power.You will notice that Jupiter's power is solely one of deflection. He cannot vie with the Sun directly in a tug of war; but he can deflect the comet and thus use the very speed imparted by the Sun against the Sun's attraction. It is like the Japanese jiu-jitsu, or scientific wrestling, of which the art consists in so adroitly turning another's strength against himself as to make the man's own momentum cause his fall.

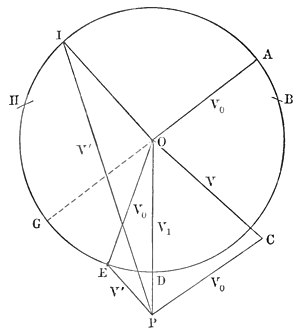
Triangle of velocities.Considering the case in this wise, we shall have the key to all of Jupiter's control. Form a triangle of velocities, of which the one side shall represent Jupiter's motion in amount and direction, a second the comet's, and the third the relative motion of the one body about the other; then draw a circle with the last for radius from the meeting-point of the planet's and comet's true motions, and join any other point of it to its centre. This second radius will represent the outgoing asymptote of the relative orbit, according to the planet's pull, while the line joining its peripheral end to Jupiter will be the comet's subsequent motion in amount and direction.

From this you will perceive that the comet's subsequent career depends upon the actual speed with which, the angle under which, and the nearness to which, it approaches the planet. If it creep upon the planet from behind, it is more likely to be captured than if it meet it head on; and if it be traveling slowly, it is more likely to be caught than if it were going fast.

Direct orbits made retrograde.Any one of many things may happen. If it pass behind the planet, its actual speed is increased, and either it is sent clean out of the system, or it is at least put farther from capture than before. If it pass before the planet and in such a way that its relative speed about the planet exceeds the planet's own motion, and it is turned round through a sufficient angle, it may, from a previously direct path about the Sun, be diverted into a retrograde one. In this case, it will commonly have a small velocity after the encounter and retrograde in a small ellipse.

FIG. XV. ACTION OF JUPITER.

$\scriptstyle V$ represents in amount and direction the comet's actual velocity in space. $\scriptstyle V_{1}$ similarly denotes that of the planet, the two bodies meeting one another under the angle $\scriptstyle VOV_{1}$. $\scriptstyle V_{0}$ will then represent the relative motion, in amount and direction, with which the comet approaches the planet.

The action of the planet is to turn the relative motion of the comet through an angle, say AOE, OA representing the in-coming asymptote of the relative orbit, OE the out-going one. EP or V' will then represent the absolute motion in space of the comet after the encounter. Similarly, if the comet passed behind the planet and was turned through the angle AOI, PI would be the new absolute velocity of the comet on leaving the planet.

The critical angle.If however, its entering speed and approaching angle, which we will call $\scriptstyle \omega$, are such that $\scriptstyle \cos {\omega }<{\frac {1}{2}}.{\frac {v}{v_{1}}},$ where $\scriptstyle v$ is its actual velocity,$\scriptstyle v_{1}$ that of the planet ; then its relative velocity ,$\scriptstyle v_{o}$, can never be greater than $\scriptstyle v_{1}$ and the resulting orbit never can become retrograde. This angle we will call the critical angle, and designate it by the symbol $\scriptstyle \chi$.

Now $\scriptstyle \omega$ we can calculate for each of the comets of Jupiter's family from their known present paths. Furthermore, since Jupiter's only effect is to swing the outgoing asymptote of the relative orbit round $\scriptstyle v_{0}$ can never be changed, and the future possible values of $\scriptstyle \omega$ have a superior limit $\scriptstyle \omega '$, which they can never pass. This also we can calculate. Doing this, and calculating also the value of $\scriptstyle \chi$ for each comet, we find the table on the opposite page.

ω and ω' both less than χ in all comets of Jupiter's family.

From the table, it appears that in every one of comets of Jupiter's family, $\scriptstyle \omega$ is within the critcal angle.

Furthermore, that $\scriptstyle \omega '$, the maximum value which $\scriptstyle \omega$ may attain under the perturbative effect of the planet, owing to the swing of the asymptotes of the hyperbolic relative orbit of the planet, is also always within $\scriptstyle \chi$

PLATE XI.		JUPITER'S COMET FAMILY
Galle's Cat. No.	Discoverer.	Inclination of orbit to ecliptic.	Major axis.	Perihelion.	Apelion	α Angle between comet's path and Jupiter.	ω′ maximum value possible for ω.	χ Critical angle.	σ Angle of stability.
64	. . . . . . . .	+ 2.9	6.14	1.1	5.0	0	0	0	0
85	. . . . . . . .	+ 1.9	6.18	.9	5.3	18.7	30.1	73.6
100	Helfenzrieder*	+ 8.0	5.88	.4	5.5	37.9	43.4	76.1
102	Lexell*	+ 1.6	6.35	.7	5.7	36.6	38.9	72.4	8.8
105	Biela	+17.1	7.10	1.0	6.1	41.3	41.4	68.5	21.1
113	Pigott*	+45.1	6.52	1.5	5.0
117	Encke	+13.6	4.42	.3	4.1
158	Winnecke	+10.7	6.32	.8	5.5	32.1	36.0	72.7	6.6
159	Blanpain*	+ 9.0	5.71	.9	4.8
200	Faye	+11.4	7.61	1.7	5.9	28.9	29.0	66.6	23.1
201	De Vico	+ 2.9	6.20	1.2	5.0
210	Bronsen	+30.9	6.29	.7	5.6	45.7	46.0	73.0	0.0
230	D'Arrest	+14.2	6.89	1.2	5.7	31.8	33.2	69.5	19.7
259	Tuttle*	+19.5	7.06	1.1	5.9	37.8	38.0	68.7	21.0
293	Tempel	+ 6.4	6.37	1.6	4.8
300	Tempel–Swift	+ 5.5	6.20	1.1	5.1
311	Tempel	+12.7	5.98	1.3	4.7
348	. . . . . . . .	+ 6.8	8.43	.7	7.7	55.3	61.0	6.40	24.3
358	Barnard*	+ 5.4	6.11	1.3	4.8
359	Wolf	+25.3	7.15	1.6	5.5	32.8	33.0
368	Brooks*	+12.9	6.32	1.3	5.0
371	Finlay	+ 3.0	7.08	1.0	6.1	38.0	38.0	68.3	21.5
388	Brooks	+ 6.1	7.37	1.9	5.4	15.8	20.0	68.7	21.2
389	. . . . . . . .	+10.2	8.36	1.4	7.0	41.7	43.0	67.5	22.5
396	Spitaler*	+12.8	6.87	1.8	5.1			64.2	24.4
404	Holmes	+20.8	7.23	2.1	5.1
406	Barnard*	+31.2	6.78	1.4	5.4	34.4	36.0	70.1	18.5
412	. . . . . . . .	+ 5.6	7.80	1.1	6.6	41.6	42.0	65.9	23.6
417	. . . . . . . .	+ 3.0	7.36	1.2	6.2	33.6	34.0	67.5	22.5
424	. . . . . . . .	+11.3	7.00	1.5	5.5	24.6	27.0	69.0	20.5
426	. . . . . . . .	+13.7	6.92	1.1	5.8	34.4	35.0	69.4	19.9
446	. . . . . . . .	+29.9	7.23	.9	6.3	49.5	50.0	68.0	22.0
⁠
Average	. . . . . . . .	12.9	6.73	1.2

Therefore, of the comets of Jupiter's comet-family, not only is none now retrograde, but none can ever become so unless some other body interfere with it.

ω nearly equals ω' in almost all cases.A singular coincidence characterizes the values $\scriptstyle \omega$ and $\scriptstyle \omega '$ In all but two cases,$\scriptstyle \omega$nearly equals $\scriptstyle \omega '$, as if for some reason $\scriptstyle \omega$ were always trying to attain this maximum as a condition of stable equilibrium. In ten cases out of twenty, or in one half of the whole, the approach is within less than ½°.

Potential relative velocity remains unchanged.It is to be noticed that in orbits potentially retrograde, the potential direct velocity is also greatest; so that both on the score of retrogradation and of greater direct velocity, comets pursuing such orbits are more subject to expulsion.

Comets of high potential relative velocity the first to disappear.In course of time, comets possessing a high potential velocity must be weeded out of the sysem sooner or later, they must meet the planet under conditions of approach which convert their high potential velocity into an actual one. This will happen the sooner for comets in proportion to their velocity possibilities. It therefore will occur more speedily for originally parabolic comets than for elliptic ones of short period; but it will require some time even for them. Either, then, Jupiter's present comet family has been of very slow growth, and each comet remains for a long time in the family, or it is made up only of short-period comets drawn from the immediate neighborhood.

Comets ephemeral things.Now, comets appear to be ephemeral things, being easily disintegrated into meteor swarms, and never abiding long in one stay. Thus the latter supposition seems on the face of it the more likely.

We may conclude provisionally that Jupiter's comet family came from the neighborhood.

Jupiter has cleared his neighborhood.It is certain that Jupiter has swept his neighborhood of such comets as do not fulfill the criterion of the angle $\scriptstyle \chi$; that is, of all the comets actually or potentially retrograde. If we consider the comet aphelia of short-period comets, we shall notice that they are clustered about the path of Jupiter and the path of Saturn, thinning out to a neutral ground between, where there are none. Two thirds way from Jupiter's orbit to Saturn's, space is clear of them, the centre of the gap falling at 8.4 astronomical units from the Sun.

Let us consider the mean comet; that is, a comet having the mean inclination of parabolic comets, the mean perihelion distance of the comets of Jupiter's family, such being the distance most likely to disclose them to us, and let this mean comet have successively aphelion distances from Jupiter's orbit to Saturn's.

Mean inclination of comets: theoretical.The mean inclination we may take either as the mean of comets coming to us from all parts of space indifferently or as the mean of such parabolic comets as have actually been observed.

If we suppose the inclinations of the cometary orbits to be equally distributed through space, then the poles of the orbits will likewise be strewn uniformly over the celestial sphere. If α be the angle made by a pole with the pole of the ecliptic, the mean inclination of the poles can be found by multiplying the number of poles at any inclination, which is as the strip of surface yielding it, by that inclination, and then dividing the integral of this for the whole sphere by the surface of the sphere. The strip of surface at any inclination a is $\scriptstyle 2\pi r^{2}\sin {\alpha }.d{\alpha }$. Whence the average inclination in radians is

$\scriptstyle {\frac {\int _{0}^{\pi }{2\pi r^{2}\sin {\alpha }.\alpha .d\alpha }}{\int _{0}^{\pi }2\pi r^{2}\sin {\alpha }.d\alpha }}=1$

or i= 57°.3.

Mean inclination observed.The second mean inclination or actual mean of all the parabolic orbits observed is i = 52°.4. It is worthy of notice how near the two are, showing that the parabolic comets come to us, practically, indifferently from all parts of space.

Calculating $\scriptstyle \omega$ and $\scriptstyle \chi$ for the successive aphelia, we find that, on the first supposition, $\scriptstyle \omega$ passes $\scriptstyle \chi$ at 8.4 astro, units; on the second, at 8.75 ditto. It is Jupiter, then, that has swept this space of comets.

Family larger than we see.Only a small fraction of Jupiter's comet family can ever come within our ken; for any comet whose perihelion lay outside of two astronomical units must, perforce, escape recognition. Invisibility would be caused both by the comet's distance from us and by its distance from the Sun, for the commotion set up in these bodies, as they near the Sun, is chiefly responsible for the display they make.

The family undoubtedly consists of many more comets with greater perihelion distance.

Jupiter is not the only planet that has a comet-family. All the large planets have the like. Saturn has a family of two, Uranus also of two, Neptune of six; and the spaces between these planets are clear of comet aphelia; the gaps prove the action.

Nor does the action, apparently, stop there. Plotting the aphelia of all the comets that have been observed, we find, as we go out from the Sun, clusters of them at first, representing, respectively, Jupiter's, Saturn's, Uranus', and Nep-

FIG. XVI. COMET APHELIA

tune's family; but the clusters do not stop with Neptune. Beyond that planet is a gap, and then at 49 and 50 astronomical units we find two more aphelia, and then nothing again till we reach 75 units out.

This can hardly be accident; and if not chance, it means a planet out there as yet unseen by man, but certain sometime to be detected and added to the others. Thus not only are comets a part of our system now recognized, but they act as finger-posts to planets not yet known.

We have thus examined the case of an old planet,—Mercury; of a middle-aged one,—Mars; of a youthful one,—Jupiter; and we have ended by envisaging the yet unchristened.