Translation:On the Theory of the Michelson Experiment
On the Theory of the Michelson Experiment.
By M. Laue.
The goal of the following investigation is to discuss the objections against the Michelson experiment given by Budde[1] in his Karlsruhe lecture, in a more closely way as it was possible in the discussion immediately after his lecture. The most severe of these objections concern the question, as to how to calculate the phase differences shown by the light ray in its given path at different points, in a system of moving bodies. This criticism of him is placed by us at the beginning. Part II is then concerned with the influence exerted by the thickness of the separation plate; part III is concerned with the location (occupied by the interferometer during the experiments) relative to Earth's velocity.
I.
Budde objects against the previously given representations (based on the one given by Lorentz) of the Michelson experiment, that there is a principal mistake in the calculation of the phase difference at which the interference takes place. Since these representations mostly neglect the thickness of the separating plate, we also want to allow us to proceed the same way here; the principal things won't be changed by that. Additionally, part II will rectify the things missed here.
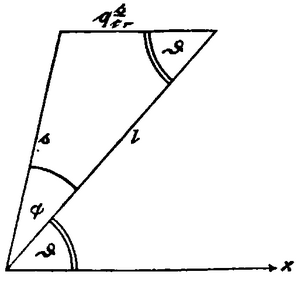
In his book concerning the relativity principle[2], the author of this response has based the criticized representation on the theorem that light traverses a distance moving with velocity , where the relative velocity is the vector difference from its absolute velocity and from . This theorem shall at first be proven extensively here. There, we use a reference system , which is to be referred to as the aether in the sense of the absolute theory, and as a valid system in the sense of relativity theory. Besides, we introduce a coordinate system
| (1) |
moving with velocity in -direction. It may not confused with a second valid reference system in the sense of relativity theory; all length and time indications are rather exclusively to be related to the measures valid in the resting system . Therefore, the following considerations are also valid in all electromagnetic theories for moving bodies. The moving distance , for which the light propagation shall be studied, shall be extended from the origin of the axes-cross to a point . Its direction is that of the relative velocity .
As mentioned above, it shall be
| ; | (2) |
if we represent these vectors by distances, then the latter are mutually located as in Fig. 1. Now, if the periodic term of light excitation for a plane wave (related to ) is
| (3) |
then are direction cosines of , so that
| (4) |

when is the angle between and the -direction. Yet according to (1) it is
| (5) |
At the starting point of distance , the oscillation is thus represented by
| , | (6) |
at endpoint by
| (7) |
According to a known theorem of analytical geometric, it is however
| (8) |
where denotes the angle between and . Furthermore it can be seen from the figure, that
| (9) |
Thus expression (7) becomes equal to
| (10) |
when
| (11) |
denotes the relative oscillation number (relative to a co-moving point). The comparison of (6) and (10) shows, that the phases traverse the moving distance with relative velocity defined by (2). It is after all quite illustrative, that the displacement of a "wave crest" (sit venia verbo) happens with respect to the moving distance with this relative velocity.
Now, the ray shall be reflected in by a mirror, so that it now traverses in its relative optical path the distance in the opposite direction. The returning wave is represented at the origin of the moving system in analogy to (6) by
| , | (12) |
at point in analogy to (10) by
| , | (13) |
is given from the construction of Fig. 1, except that its direction is opposite to that of ; is a number still to be specified. That the relative frequency is maintained at the reflection, follows from the presence of linear limiting conditions, which connect the incident wave with the reflected one. They can only be satisfied, when the periodic functions (10) and (13) representing both waves at point , are mutually connected by[3]
| (14) |
would be the phase transition at the reflection; if one neglects this, as it is done by Budde – this assumption is without influence on the result –, one additionally finds from (14)
| (15) |
Thus according to (12), the returning oscillation is represented in the origin by
| (16) |
i.e., the phases require the time to traverse distance back and forth. Herein lies in my view the irrefutable justification of the present theory.
The question remains undecided, whether (for the calculation of the phase difference) one has to divide the difference of the times calculated for both in this way, by the relative period:
| (17) |
or by the absolute period present at the end:
| ; | (18) |
as to this effect of second order, the difference between them plays no role.
It is completely identical with the given procedure for time calculations, when one speaks about traversing the absolute optical path with velocity . Because the absolute optical path emerges from distance and velocity by the construction in Fig. 2., which is similar to Fig 1, so that
| (19) |
A third procedure would be,
to divide distance by the relative wave length
| (20) |
According to (6) and (16),
directly gives the phase difference present in the zero point between the waves traveling for- and backwards. Since is conserved at every reflection, varies proportional to .
Instead of these three valid procedures, Budde employs a fourth one; he divides any absolute optical path by the corresponding wave length
| (21) |
The sum of two of such ratios shall represent the phase difference between the waves traveling for- and backwards for one of the points of the separating plate. and vary from distance to distance in accordance with Doppler's principle.
Already in the supplement to my discussion remarks[4] (of the two possibilities mentioned there, the second one applies here) I have alluded to the fact, that such a sum is not proportional to the traversing time of the phases, and that therefore the difference of two such sums (at that place simply written as , in which the distances related to the second ray, are calculated negatively) are not in any relation to the phase difference. The reply of Budde[5], that it is always , is indeed correctly per se, but it doesn't affect my objection; not every traversing time is to be divided by the corresponding period , but the division is to be executed in all of them through period or being present at the end (see above).
In the discussion, however, Budde has supported his way of calculation by a figure not printed, which should have given a scheme for the appearance of two wave trains, which (starting from one point) eventually encounter again on different ways in terms of their absolute optical path and with some changes of wave length. For example, if one wave train has a length of 166 and the other one 166½ wave lengths, then they interfere with phase difference ; thus is his conclusion. However, what shall this figure represent? Evidently the spatial distribution of the oscillations in a certain moment. Yet this is not the case, since the absolute optical path is replaced by the same velocity as the apparatus. The different parts of the paths traversed by the wave train, therefore have no meaning for the representation of the oscillation state in a certain moment. It is not even necessary, that light excitation is simultaneously present on all these parts at all. At great arm lengths and great velocity, this wouldn't be the case.[6]
If one wants to correctly describe the thought on which the figure is based, then one has to draw the relative optical paths with the wave trains lying upon them, and by that one comes to the third of the previous procedures, at which one divides every distance by the relative wave length lying upon them, and to sum up the ratios.
Besides this principal objection against Budde's way of calculation, we also must express still another objection against a single point of this calculation, from which (despite its subordinate importance) nevertheless the correctness of the result is depending.
Budde namely sets in equation (1) the ratio of the absolute wave lengths before and after the reflection of the moving mirror ( and )[7], up to terms of third and higher order.
there, is the angle formed by the motion of the mirror with its normal directed in the direction of the side of light, and is the angle of incidence. As to how this equation came about, cannot exactly be seen from Budde's specification. It seems to me, that it is already incorrect in the terms of second order, as well as for the special values of appearing at the interferometer of Michelson.
To show this, we start from the formulas given by Abraham[8] for the Doppler effect and the reflection law at a moving mirror. Abraham's equation (11b) then says:
| (22) |
while according to his equation (15e)
| (23) |
There, means the ratio from the velocity component of the mirror in the direction of its normal, and , and are the cosines of the angles of incidence and reflection. Thus it is
| (24) |
From (23) we take by differentiation with respect to at constant , that
and in case , in which ,
.
Thus the series expansion holds:
| (25) |
However, from (22) and from (24) and (25) it follows:
which doesn't agree with Budde's equation – also in the special case that = 45°.
II.
We now come to speak about the influence exerted by the finite thickness of the separating plate. It is certainly to be appreciated, that Budde alludes to the necessity to study its influence as well. However, he surely overlooks at this occasion an essential part in the installation of the interferometer. In his Fig. 1 he namely shows, that (in his opinion) both surfaces of these plates are reflecting uniformly, and when he explains that the rays (emerging from one ray at the separation) are passing at a certain distance from each other at the end, then also this is based on the same opinion. Yet this is by no means correct. The reflection ability with respect to any interferometer at one side of the plate (the side can change depending on the circumstances), is rather increased[9] by silvering thus far, so that the reflected and passing ray have approximately the same brightness. The reflection at the other side which is not silvered, is comparatively unimportant. The purpose of this measure mainly consists in suppressing (as far as possible) the plan-parallel rings occurring otherwise at the plates, which would superimpose the planned interference fringes in a disturbing way. However, in this way, one of both beams traverses the plate two times after the separation, the other one not at all. The compensating plate which must be traversed two times by the latter, serves to balance this. And although we (as with Budde) aren't required to include it to the essential parts of the apparatus, it may be at least included in our considerations, since it was actually there.
Before this, we have to allude to a point in Budde's calculation, from which the result is essentially depending, and which seems problematic to us. Already when Budde begins:[10] "Then the relative velocity in glass, at which the first beam arrives in , is . The relative velocity in glass is thus ", then this is surely an unjustified generalization of the theorem being valid for resting bodies, that the speed of light within bodies is related to that in vacuum inversely as the refraction index ( namely is presupposed as the value for the refraction index in glass). If it is assumed that this were correct, then one shall change (maintaining the direction of the beam) the direction of the limiting surface; by that, also the direction of the beam incident from vacuum is changing, thus also the relative velocity of light upon it is changing; thus this is also the case for the velocity in glass according to the generalized theorem, which is evidently impossible when the beam direction is maintained. This theorem is actually not in agreement with any of the electromagnetic theories of moving bodies.
If we now want to compare with each other the statements of the absolute theory and of relativity theory concerning the influence of the plate thickness under consideration of terms of second order in , then this would be a quite difficult task, because the absolute theory is only developed under consideration of terms of first oder.[11] However, the fortunate remark of Budde helps us here, by which the ratio of the plate thickness to the length of the arms of the interferometer, is of the same magnitude as . Thus if one wants to calculate the times required by the phases to traverse both plates, then one only needs to consider the terms proportional to themselves. Because in all statements concerning terms of first order in , both theories are in full agreement.[12] The influence of plate thickness thus cannot lead to a decision between them. Additionally, one understands without further ado, that it doesn't change anything according to relativity theory, when one replaces an infinitely thin separating plate in the apparatus by a plate of thickness , and simultaneously turns on the compensating plate.
That all relevant reflections at the separating plate occur at the same surface, has by the way the success, that the beam displacement , of which Budde speaks, vanishes. By that, all consequences and modifying proposals connected with that seem irrelevant to me. By another reason, however, all mutually corresponding beams don't coincide at the end; namely because in the experiment discussed, not fringes of equal inclination, but such ones of equal thickness are produced at a layer of air, whose one surface is formed by one mirror, and whose other surface is formed by a mirror image of the other mirror drawn at the separating plate. Nevertheless these beams come to interfere when one adjusts the telescope to this layer of air.[13]
III.
Contrary to both remarks previously discussed, we have to admit the validity of the third remark of Budde. The velocity of Earth against the aether indeed has an unknown component: the velocity by which Earth is moving against the aether. That this one is sometimes identified in the literature with the known motion of the sun against the fixed stars, is an assumption which only finds weak support by the fact, that there is presently no reason to ascribe to the complete system of fixed stars a motion relative to the aether. Nevertheless, in the sense of the absolute theory, we can say something about the amount of the velocity in question: it cannot be essentially greater than the velocity of Earth against the Sun. Otherwise, some of the effects of second order must have been observed at terrestrial or astronomical observations in the planetary system, which according to this theory must be present at almost all electromagnetic and optical phenomena. Thus the two possibilities remain to discuss, first, that the velocity of sun–aether is of the same magnitude as the velocity earth–planetary system, and second, that the latter is essentially greater.
In the second of these cases, we can evidently totally neglect the first velocity. However, in accordance with the first of these two possibilities, one has to add a component of same magnitude to the velocity between earth and the planetary-system; then in general a velocity of same order arises again, so that the ordinary assumption concerning the amount of the velocity earth–aether remains correct in terms of magnitude. The direction of the resulting velocity is, however, unknown to a large extent, we can only say that it must considerably change in the course of a year. Although Morley and Miller[14] have apparently overlooked this, there is still no reason to doubt the conclusiveness of their experiment. Because one hundredth of the expected fringe displacement couldn't be missed in the observation. To explain the lack of this in the course of so many repeated experiments, by an unfortunate accident with respect to the direction of the velocity earth–aether, is an assumption of much too low probability.
Munich, Institute for Theoretical Physics, March 1912.
(Received March 25, 1912.)
- ↑ E. Budde, this journal. 12. 979, 1911.
- ↑ M. Laue, Das Relativitätsprinzip (Braunschweig 1911), p. 14.
- ↑ M. Abraham, Ann. d. Phys. 14, 236, 1904.
- ↑ This journal, 12, 990, 1911.
- ↑ The same page, last line.
- ↑ For example, one shall try to represent the path traversed by a phase, not only schematically in one dimension, but with the direction corresponding to the device. The separating line of the apparatus must necessarily be drawn in two positions, so that the figure impossibly can represent the state in this moment.
- ↑ The change in the mode of denotation with respect to Budde's lecture, has the purpose to avoid confusions with the path lengths .
- ↑ M. Abraham, Ann. d. Phys. 14, 236, 1904. Here, relativity theory is not used, yet all results also apply to it.
- ↑ A. A. Michelson, Light waves and their uses, pag. 40 (Chicago 1903). The silvering is also indicated in Fig. 1. in Morley a. Miller, Phil. Mag. 9, 680, 1905.
- ↑ l. c., p. 983, left below.
- ↑ H. A. Lorentz, Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern. Leiden 1895. (Reprint: Leipzig 1906.)
- ↑ Only at magnetizable bodies a difference exists, which possibly stems, however, from a incompleteness of the formulation of the absolute theory, see. H. Minkowski, Gött. Nachr. 1908, p. 53, § 9.
- ↑ M. Laue, Ann. d. Phys. 33, 186, 1910.
- ↑ Morley a. Miller, Phil. Mag. 9, 680, 1905.
![]()
![]() This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
| Original: |
This work is in the public domain in the United States because it was published before January 1, 1929. The longest-living author of this work died in 1960, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 63 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
Public domainPublic domainfalsefalse |
|---|---|
| Translation: |
This work is released under the Creative Commons Attribution-ShareAlike 3.0 Unported license, which allows free use, distribution, and creation of derivatives, so long as the license is unchanged and clearly noted, and the original author is attributed.
Public domainPublic domainfalsefalse |














































































