Translation:The Theory of Relativity and Lobachevskian Geometry
The Theory of Relativity and Lobachevskian Geometry
By V. Varićak
In a lecture on the first period of the development of non-euclidean geometry, that was held by me on March 16, 1907 in the ceremonious year session of the Yugoslav Academy of Sciences and Arts at Agram,[1] I also mentioned the investigations concerning the admissible curvature measure of space or the length of the absolute unit distance of hyperbolic space.
All lengths with which we are concerned vanish against the unit distance and therefore the formulas of Lobachevskian geometry reduce themselves in regions of our empirical space to expressions of ordinary euclidean geometry. To make clear the relation of those geometries by an analogy from physics, I alluded to the relation of the mechanics of electrons to Newtonian mechanics.[2]
The Lorentz-Fitzgerald hypothesis of electron contraction led me to the assumption, whether this contraction could be interpreted as a consequence of geometrical anisotropy of space. It seemed to me that this contraction is analogues to the deformation of lengths in a very familiar interpretation of Lobachevskian geometry.[3] Now it seems that my assumption of the connection of non-euclidean geometry with relativity theory can be realized. The appearance of a work by Herglotz[4] urged me to immediately publish the following remarks, as his work in one point partially goes into the same direction as the related investigations of mine. The actual content of my report is of course completely different.
1. The substitution
[edit]This substitution paved me the way to the non-euclidean interpretation of relativity theory. Now, subsequently I noticed that Minkowski[5] once put
that is the expression of the velocity relation as tangens hyperbolicus, but he didn't pay further attention to the middle term of this relation.
J. J. Thomson[6] has expressed the relation of the electron's velocity to the velocity of light as the sinus of a certain angle θ. If I define this angle as a complement to the parallel angle belonging to length U, then I again arrive at that substitution. The various ways upon which we arrive at this substitution, are increasing the confidence in it.
During the composition of velocities and enclosing the angle α, we have to construct the Lobachevskian triangle with sides and with the enclosed angle π-α. The length U of measure unit u is attributed to the velocity v by the relation
| (1) |
Following the English style of writing denotes the inverse function of the hyperbolic tangent. Now we want to investigate whether this definition is not in sharp contrast to the ordinary illustration of velocities. The distances proportional to the relevant velocities are used in ordinary mechanics as representing the velocities of uniform motions. Formula (1) leads to the same result at the limits of our ordinary experience. Only at velocities nearly comparable to the velocity of light, a notable difference occurs that quickly leads to infinite distortion. As unit distance we use the path of light in one second. Then
| (2) |
If we take v = 1 km/sec at first, then
| (3) |
If we neglect everything after the first term on the right-hand side, then we commit an error that not even exerts an influence upon the 10th decimal. So by our definition, we have for a velocity of 1 km/sec a length of 1 km as the representative.
If we take the velocity of 100 km/sec which is in any case an extremely high velocity in ordinary mechanics, then it is given and the representative length U is by the way about 3mm greater then 100km. The velocity of 100000 km/sec corresponds to a length of 103700 km.
We additionally consider two velocities of β-rays calculated in the famous experiments of Kaufmann, and to which the velocity relations 0,7202 and 0,9326 are connected. They amount ca. 216060 and 279780 km/sec and they were represented by the lengths of 272400 and 503400 km.
For v = c we have U = ∞.
In graphical illustration these relations can be easily summarized.

If we take u as abscissa and as ordinate, then (1) will be represented by curve T. The straight line G or the first term in the infinite row (2), corresponds to the ordinary definition . The straight line is the inflexion tangent of T in O, so it fits well to the curve in the very far surrounding of the coordinate origin.
Fig. 1 can provide us good services for the composition of velocities. In addition to the resultant length U we can immediately take the corresponding velocity v from the figure.
If the velocities and enclose the angle α = 0, i.e. if they lie in the same direction, then . The resultant velocity follows from the formula
or
Although the resultant is smaller as the sum of the components, it will be represented (as in ordinary mechanics) by a length equal to the sum of the lengths representing the components. It is namely in this case .
The figure in the 6th Göttingen lecture by Poincaré is not in agreement with this definition.[7]
If we compose two equal velocities to which corresponds the length , then the resultant will be represented by the length .
2. Lorentz-Einstein transformation as translation
[edit]We take this transformation in the form as it was given by me.[8]
| (4) |
The variables x, y, z, l I interpret as homogeneous Weierstrass coordinates in Lobachevskian three-dimensional space. If X, Y, Z are Lobachevskian right angled coordinates, ξ, η ζ the perpendiculars that fall from point M upon the planes of the right angles coordinate system, and r is the distance of that point from the coordinate origin, then we get the following equations from the easily constructed figure
| (5) |
| (6) |
| (7) |
| (8) |
These Weierstrass coordinates satisfy, as it is easily seen, the quadratic equation[9]
| (9) |
This is therefore the invariant of first kind of the transformation defined by equations (4), or by
| (10) |
If we take
| (11) |
then we get to distance areas[10]
| (12) |
and
| (13) |
Their center planes are the coordinate planes XZ and XY.
The Lorentz-Einstein transformation can be interpreted as a translation through the intersection line of these two equidistant areas.
To simplify matters we put Z = 0 and thus the Weierstrass coordinates of a point in the plane become
| (14) |
The Lorentz-Einstein transformation
| (15) |
defines the motion along the distance line Y = b, having the X-axis as its center line. The parameter b is arbitrary.
The displacement by the distance s along that equidistant line is defined by the equations[11]
| (16) |

Here, s is the arc of that distance line. If u is its projection in the X-axis, then
| (17) |
thus
| (18) |
By multiplication of the first equations by
it is given
| (19) |
According to Fig. 2 we have in addition
| (20) |
or
| (21) |
If we consider equations (14), then we can bring (19) and (20) into the form
and those are of course the equations (15) of the Lorentz-Einstein transformation.
3. Local time
[edit]If M and are two observers moving with uniform but different velocities, then each of them can claim with the same justification, the he is at rest relative to empty space. However, that the observer in M is using a different time calculation as the observer in , can be seen from the figure above, because r is different from . The hyperbolic cosine of the radius vector of the point, at which the observer is located, is according to our conception his local time. The conception of the new notion of time[12] will be essentially simplified by our interpretation. It nearly acts intuitive. It only remains to investigate, if it is able to accomplish the same as the simple and suggestive coordinate transformation of Minkowski.
Point M can take any location on that distance line. We take it so that u will be equal to its abscissa, i.e., point M falls into the intersection point of the distance line with the ordinate axis, or we move the coordinate origin to .

The space-time transformation that is caused by a uniform motion of velocity will be completely characterized by the Weierstrass coordinates of point M. We have to put NN' = ON = u. This special case that is illustrated in Fig. 3, forces us to take the hyperbolic cosine of its Lobachevskian abscissa as the time unit of the observer at a certain point of the distance line.
For the observers in M and (Fig. 2) are the related time units
| (22) |
We see from the right angled triangle OMN and , that
or
| (23) |
is constant. If we again take observer in the intersection line of the distance line with the ordinate axis (Fig. 3), then his time unit is , while the time unit τ of the observer in M will be equal to . It is thus
| (24) |
Formula (23) gives
| (25) |
and that is the result of Einstein's investigation.[13]
The relation that is illustrated in formula (23) and Fig. 3 will be distorted, if we make a displacement of the coordinate origin upon the ordinate axis. The line ceases to be a distance line with the abscissa axis as center line. The -axis comes more and more closer to it, intersects it and then leaves it into infinity. The -axis goes away in the same manner. The Lines have the ordinate axis Y as their common perpendicular, thus in Lobachevskian geometry they move the further away from each other, the further they were elongated.

4. Uniform motion
[edit]During translations along the distance lines to the X-axis, the bunch of perpendiculars to the X-axes remain unchanged and vice versa. The invariants of second kind of the infinitesimal transformation (10) are those perpendiculars
| (26) |
as it is
In Lobachevskian right angled coordinates the equation of the perpendicular in the point (u,0) is
| (27) |
If we substitute this in formulas (14), then we have
and from this we immediately obtain equation (26).
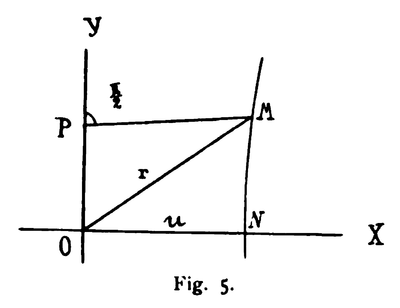
During uniform motion the relation between the unit of distance and the unit of time is equal to the unit of velocity. Thus it is
or
The image of uniform motion is the perpendicular to the X-axis (Fig. 5). By the coordinate transformation as indicated in Fig. 4, also the uniformity of motion is canceled.
According to Minkowski the world line illustrating uniform motion, is the straight line in the xt-plane trough the coordinate origin.
In this connection the following thought of Palagyi[14] is interesting: "What we consider as the path traveled by the material point within a space imagined as stationary, is only the apparent path of the point; the real path results from the construction of the right angled parallelogram of the apparent path and the elapsed time ... This had to be a consequence of the fact, that even the state of rest was interpreted by us as uniform motion, and specifically as a motion in the subjective dimension of time. Thus by the parallelogram we put together this subjective component with the objective component that is given by the apparent path, and thus we get the real path traveled by the point in streaming space.
This real way together with the time ray constitutes an angle φ, that I call the time angle of uniform motion."
The velocity was expressed by him by the tangent of time angle φ.
The image of accelerated motion is the distance line. To its intersection with the ordinate axis we attribute the velocity 0; in its additional points we have
The velocity increases together with the distance up to the velocity of light.
5. The principle of Doppler
[edit]In my first work on the non-euclidean interpretation of relativity theory[15] I transformed the first formula of Einstein for the Doppler principle into the form
| (28) |
We take two equidistant lines (Fig. 6) with the X-axis as their common center line and with the parameters . The arcs of those two distance lines limited by the Y-axis and the perpendicular to the X-axis in point C, are
Thus it is
| (29) |

The relation between frequencies and can be illustrated in the general case as the relation of the arcs of two distance lines between common perpendiculars.
For φ = 0 we have . The distance lines go over into the limiting circles with the common axes, and we have
| (30) |
Fig. 7 corresponds to that case.

In euclidean geometry the distance lines and the limiting circles are reduced to parallels to the given straight line. The expressions for Doppler's principle in ordinary mechanics can be easily illustrated by intersections of parallel transversals between the legs of an angle.
6. Aberration
[edit]The light ray T strikes the X-axis under the angle φ. To find the direction of the deflected light ray, we have to draw a Lobachevskian parallel from N to T. The aberration equation is
| (31) |
The construction of the needed parallel is executed in Fig. 8 as follows.[16]

As point U always lies between S and R, it can be easily seen from the figure that in relativity theory is smaller than of ordinary mechanics.
In Einstein's formula for aberration,
| (32) |
we denote the cosines on the left-hand side and in the numerator of the fraction by corresponding sines, then we square and get in this way after some transformations
| (33) |
During the motion of earth in its orbit relative to the fixed stars as reference frame we have .[17] For such small velocities we can neglect , and then we obtain
| (34) |
Formula (34) and formula (32), in which we will take instead of , give
| (35) |
from which we can, in accordance with the ordinary theory, easily find the formula
| (36) |
By comparison of formulas (33) and (34) we find
| (37) |
However, if we take in Fig. 3 , then we can put
| (38) |
If would even be better, if Fig. 1 of my first treatise is used. Then we can take
| (39) |
7. Light pressure
[edit]The following remarks are related to Einstein's formulas located in § 8 of his first paper on the relativity principle[18]. We can easily see that
| (40) |
and this can be interpreted, as earlier , by using Fig. 6.
For light pressure, Einstein gave the formula
| (41) |
We transform them at first into the form
from which we easily obtain
| (42) |
If we take a Lobachevskian right angled triangle with hypotenuse and an acute angle , then we obtain for the side adjacent to angle α, the expression
| (43) |
hence
| (44) |
- Agram, February 12, 1910
(Received February 18, 1910)
- ↑ Published in "Rad jugoslavenske akademije" 169, 110-194, 1907.
- ↑ l.c., p. 172.
- ↑ My remarks on that interpretation were published in "Rad jugoslavenske akademije" 154, 81-131, 1903. With this interpretation is also conerned A. Schwarz: Zur Theorie der reellen linearen Transformationen und der Lobatschefskijschen Geometrie, Wien, Sitzungsb., II. Abt., 99, 1890. Bonolas, Index operum ad geometriam absolutam spectantium, in Klausenburger Festschrift, is not mentioned in that treatise.
- ↑ Herglotz, Über den vom Standpunkt des Relativitätsprinzips aus als "starr" zu bezeichnenden Körper. Ann. der Phys. 31, 383, 1910
- ↑ Minkowski, Die Grundgleichungen usw., Göttinger Nachrichten, p. 59, 1908
- ↑ Lodge, Elektronen, p. 120
- ↑ H. Poincaré, Sechs Vorträge aus der reinen Mathematik und mathematischen Physik, 1910, p. 52
- ↑ This journal. 11, 93, 1910
- ↑ For these coordinates see Liebmann, Nichteuklidische Geometrie, p. 166, and Killing, Die nichteuklidischen Raumformen.
- ↑ The general equation of the distance area was given by me in a treatise in "Rad jugoslavenske akademije" 175, 215-240, 1908. There, the middle plane was defined by the ends ξ, η and the angle α. For the determination of the plane see my work: Zur nichteuklidischen analytischen Geometrie in Attil del IV congresso dei matematici, Roma 1909, 2, 213-226.
- ↑ Concerning the transformation of the Lobachevskian plane see my relevant papers in "Rad jugoslavenske akademije" 165, 50-80, 236-344, 1906, or the short excerpt from it in Jahresber. d. deutsch. Mathematikerver. 17, 70-83, 1908.
- ↑ Planck, Acht Vorlesungen über theoretische Physik, p. 117, says that this new conception of the notion of time surpasses in boldness everything previously suggested in speculative natural phenomena and even in the philosophical theories of knowledge: non-euclidean geometry, which only comes seriously into consideration in pure mathematics, would be child's play in comparison.
- ↑ A. Einstein, Zur Elektrodynamik bewegter Körper. Ann. d. Phys. 17, 904, 1905
- ↑ Palagyi, Neue Theorie des Raumes und der Zeit, 1901, p. 45.
- ↑ This journal. 11. 93, 1910
- ↑ Lobatschevskij-Engel, Zwei geometrische Abhandlungen, p. 256
- ↑ Brill, Einführung in die Mechanik, 1909, p. 206.
- ↑ Ann. der Phys. 17, 913-915. 1905
![]()
![]() This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
| Original: |
This work is in the public domain in the United States because it was published before January 1, 1929. The longest-living author of this work died in 1942, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 81 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
Public domainPublic domainfalsefalse |
|---|---|
| Translation: |
This work is released under the Creative Commons Attribution-ShareAlike 3.0 Unported license, which allows free use, distribution, and creation of derivatives, so long as the license is unchanged and clearly noted, and the original author is attributed.
Public domainPublic domainfalsefalse |






























































































