1911 Encyclopædia Britannica/Map
MAP, a representation, on a plane and a reduced scale, of part or the whole of the earth’s surface. If specially designed to meet the requirements of seamen it is called a chart, if on an exceptionally large scale a plan. The words map and chart are derived from mappa and charta, the former being the Latin for napkin or cloth, the latter for papyrus or parchment. Maps were thus named after the material upon which they were drawn or painted, and it should be noted that even at present maps intended for use in the open air, by cyclists, military men and others, are frequently printed on cloth. In Italian, Spanish and Portuguese the word mappa has retained its place, by the side of carta, for marine charts, but in other languages both kinds of maps[1] are generally known by a word derived from the Latin charta, as carte in French, Karte in German, Kaart in Dutch. A chart, in French, is called carte hydrographique, marine or des côtes; in Spanish or Portuguese carta de marear, in Italian carta da navigare, in German Seekarte (to distinguish it from Landkarte), in Dutch Zeekaart or Paskaart. A chart on Mercator’s projection is called Wassende graadkaart in Dutch, carte réduite in French. Lastly, a collection of maps is called an atlas, after the figure of Atlas, the Titan, supporting the heavens, which ornamented the title of Lafreri’s and Mercator’s atlases in the 16th century.
Classification of Maps.—Maps differ greatly, not only as to the scale on which they are drawn, but also with respect to the fullness or the character of the information which they convey. Broadly speaking, they may be divided into two classes, of which the first includes topographical, chorographical and general maps, the second the great variety designed for special purposes.
Topographical maps and plans are drawn on a scale sufficiently large to enable the draughtsman to show most objects on a scale true to nature.[2] Its information should not only be accurate, but also conveyed intelligibly and with taste. Exaggeration, however, is not always to be avoided, for even on the British 1 in. ordnance map the roads appear as if they were 130 ft. in width.
Chorographical (Gr. χώρα, country or region) and general maps are either reduced from topographical maps or compiled from such miscellaneous sources as are available. In the former case the cartographer is merely called upon to reduce and generalize the information given by his originals, to make a judicious selection of place names, and to take care that the map is not overcrowded with names and details. Far more difficult is his task where no surveys are available, and the map has to be compiled from a variety of sources. These materials generally include reconnaissance survey of small districts, route surveys and astronomical observations supplied by travellers, and information obtained from native sources. The compiler, in combining these materials, is called upon to examine the various sources of information, and to form an estimate of their value, which he can only do if he have himself some knowledge of surveying and of the methods of determining positions by astronomical observation. A knowledge of the languages in which the accounts of travellers are written, and even of native languages, is almost indispensable. He ought not to be satisfied with compiling his map from existing maps, but should subject each explorer’s account to an independent examination, when he will frequently find that either the explorer himself, or the draughtsman employed by him, has failed to introduce into his map the whole of the information available. Latitudes from the observations of travellers may generally be trusted, but longitudes should be accepted with caution; for so competent an observer as Captain Speke placed the capital of Uganda in longitude 32° 44′ E., when its true longitude as determined by more trustworthy observations is 32° 26′ E., an error of 18′. Again, on the map illustrating Livingstone’s “Last Journals” the Luapula is shown as issuing from the Bangweulu in the north-west, when an examination of the account of the natives who carried the great explorer’s remains to the coast would have shown that it leaves that lake on the south.
The second group includes all maps compiled for special purposes. Their variety is considerable, for they are designed to illustrate physical and political geography, travel and navigation, trade and commerce, and, in fact, every subject connected with geographical distribution and capable of being illustrated by means of a map. We thus have (1) physical maps in great variety, including geological, orographical and hydrographical maps, maps illustrative of the geographical distribution of meteorological phenomena, of plants and animals, such as are to be found in Berghaus’s “Physical Atlas,” of which an enlarged English edition is published by J. G. Bartholomew of Edinburgh; (2) political maps, showing political boundaries; (3) ethnological maps, illustrating the distribution of the varieties of man, the density of population, &c.; (4) travel maps, showing roads or railways and ocean-routes (as is done by Philips’ “Marine Atlas”), or designed for the special use of cyclists or aviators; (5) statistical maps, illustrating commerce and industries; (6) historical maps; (7) maps specially designed for educational purposes.
Scale of Maps.—Formerly map makers contented themselves with placing upon their maps a linear scale of miles, deduced from the central meridian or the equator. They now add the proportion which these units of length have to nature, or state how many of these units are contained within some local measure of length. The former method, usually called the “natural scale,” may be described as “international,” for it is quite independent of local measures of length, and depends exclusively upon the size and figure of the earth. Thus a scale of 1: 1,000,000 signifies that each unit of length on the map represents one million of such units in nature. The second method is still employed in many cases, and we find thus:—
| 1 | in. | = | 1 | statute mile (of 63,366 in.) | corresponds to | 1 | : | 63,366 | ||||
| 6 | in. | = | 1 | ,, | ,, | ,, | ,, | 1 | : | 10,560 | ||
| 1 | in. | = | 5 chains (of 858 in.) | . | . | ,, | 1 | : | 4,890 | |||
| 1 | in. | = | 1 nautical mile (of 73,037 in.) | . | ,, | 1 | : | 73,037 | ||||
| 1 | in. | = | 1 verst (of 42,000 in.) | . | . | ,, | 1 | : | 42,000 | |||
| 2 Vienna in. = 1 Austrian mile (of 288,000 in.) | ,, | 1 | : | 144,000 | ||||||||
| 1 | cm. | = | 500 metres (of 100 cm.) | . | . | ,, | 1 | : | 50,000 | |||
In cases where the draughtsman has omitted to indicate the scale we can ascertain it by dividing the actual length of a meridian degree by the length of a degree measure upon the map. Thus a degree between 50° and 51° measures 111,226,000 mm.; on the map it is represented by 111 mm. Hence the scale is 1:1,000,000 approximately.
The linear scale of maps can obviously be used only in the case of maps covering a small area, for in the case of maps of greater extension measurements would be vitiated owing to the distortion or exaggeration inherent in all projections, not to mention the expansion or shrinking of the paper in the process of printing. As an extreme instance of the misleading character of the scale given on maps embracing a wide area we may refer to a map of a hemisphere. The scale of that map, as determined by the equator or centre meridian, we will suppose to be 1:125,000,000, while the encircling meridian indicates a scale of 1:80,000,000; and a “mean” scale, equal to the square root of the proportion which the area of the map bears to the actual area of a hemisphere, is 1:112,000,000. In adopting a scale for their maps, cartographers will do well to choose a multiple of 1000 if possible, for such a scale can claim to be international, while in planning an atlas they ought to avoid a needless multiplicity of scales.
Map Projections are dealt with separately below. It will suffice therefore to point out that the ordinary needs of the cartographer can be met by conical projections, and, in the case of maps covering a wide area, by Lambert’s equal area projection. The indiscriminate use of Mercator’s projection, for maps of the world, is to be deprecated owing to the inordinate exaggeration of areas in high latitudes. In the case of topographical maps sheets bounded by meridians and parallels are to be commended.
The meridian of Greenwich has been universally accepted as the initial meridian, but in the case of most topographical maps of foreign countries local meridians are still adhered to—the more important among which are:—
| Paris (Obs. nationale) | . | . | 2° 20′ 14″ E. | of Greenwich. | ||
| Pulkova (St Petersburg) | . | 30° 19′ 39″ E. | ,, | |||
| Stockholm | . | . | . | . | 18°3′ 30″ E. | ,, |
| Rome (Collegio Romano) | . | 12° 28′ 40″ E. | ,, | |||
| Brussels (Old town) | . | . | 4° 22′ 11″ E. | ,, | ||
| Madrid . | . | . | . | . | 3° 41′ 16″ W. | ,, |
| Ferro (assumed) | . | . | . | 20°0′0″ W. | of Paris. | |
The outline includes coast-line, rivers, roads, towns, and in fact all objects capable of being shown on a map, with the exception of the hills and of woods, swamps, deserts and the like, which the draughtsman generally describes as “ornament.” Conventional signs and symbols are universally used in depicting these objects.
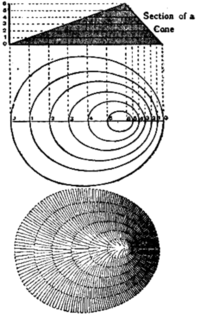
Delineation of the Ground.—The mole-hills and serrated ridges of medieval maps were still in almost general use at the close of the 18th century, and are occasionally met with at the present day, being cheaply produced, readily understood by the unlearned, and in reality preferable to the uncouth and misleading hatchings still to be seen on many maps. Far superior are those scenographic representations which enable a person consulting the map to identify prominent landmarks, such as the Pic du Midi, which rises like a pillar to the south of Pau, but is not readily discovered upon an ordinary map. This advantage is still fully recognized, for such views of distant hills are still commonly given on the margin of marine charts for the assistance of navigators; military surveyors are encouraged to introduce sketches of prominent landmarks upon their reconnaissance plans, and the general public is enabled to consult “Picturesque Relief Maps”—such as F. W. Delkeskamp’s Switzerland (1830) or his Panorama of the Rhine. Delineations such as these do not, however, satisfy scientific requirements. All objects on a map are required to be shown as projected horizontally upon a plane. This principle must naturally be adhered to when delineating the features of the ground. This was recognized by J. Picard and other members of the Academy of Science whom Colbert, in 1668, directed to prepare a new map of France, for on David Vivier’s map of the environs of Paris (1674, scale 1:86,400) very crude hachures bounding the rivers have been substituted for the scenographic hills of older maps. Little progress in the delineation of the ground, however, was made until towards the close of the 18th century, when horizontal contours and hachures regulated according to the angle of inclination of all slopes, were adopted. These contours intersect the ground at a given distance above or below the level of the sea, and thus bound a series of horizontal planes (see fig. 1). Contours of this kind were first utilized by M. S. Cruquius in his chart of the Merwede (1728); Philip Buache (1737) introduced such contours or isobaths (Gr. ἶσος, equal; βαθύς, deep) upon his chart of the Channel, and intended to introduce similar contours or isohypses (ὕψος, height) for a representation of the land. Dupain-Triel, acting upon a suggestion of his friend M. Ducarla, published his La France considérée dans les différentes hauteurs de ses plaines (1791), upon which equidistant contours at intervals of 16 toises found a place. The scientific value of these contoured maps is fully recognized. They not only indicate the height of the land, but also enable us to compute the declivity of the mountain slopes; and if minor features of ground lying between two contours—such as ravines, as also rocky precipices and glaciers—are indicated, as is done on the Siegfried atlas of Switzerland, they fully meet the requirements of the scientific man, the engineer and the mountain-climber. At the same time it cannot be denied that these maps, unless the contours are inserted at short intervals, lack graphic expression. Two methods are employed to attain this: the first distinguishes the strata or layers by colours; the second indicates the varying slopes by shades or hachures. The first of these methods yields a hypsographical, or—if the sea-bottom be included, in which case all contours are referred to a common datum line—a bathy hypsographical map. Carl Ritter, in 1806, employed graduated tints, increasing in lightness on proceeding from the lowlands to the highlands; while General F. von Hauslab, director of the Austrian Surveys, in 1842, advised that the darkest tints should be allotted to the highlands, so that they might not obscure details in the densely peopled plains. The desired effect may be produced by a graduation of the same colour, or by a polychromatic scale—such as white, pale red, pale brown, various shades of green, violet and purple, in ascending order. C. von Sonklar, in his map of the Hohe Tauern (1:144,000; 1864) coloured plains and valleys green; mountain slopes in five shades of brown; glaciers blue or white. E. G. Ravenstein’s map of Ben Nevis (1887) first employed the colours of the spectrum, viz. green to brown, in ascending order for the land; blue, indigo and violet for the sea, increasing in intensity with the height or the depth. At first cartographers chose their colours rather arbitrarily. Thus Horsell, who was the first to introduce tints on his map of Sweden and Norway (1:600,000; 1835), coloured the lowlands up to 300 ft. in green, succeeded by red, yellow and white for the higher ground; while A. Papen, on his hypsographical map of Central Europe (1857) introduced a perplexing range of colours. At the present time compilers of strata maps generally limit themselves to two or three colours, in various shades, with green for the lowlands, brown for the hills and blue for the sea. On the international map of the world, planned by Professor A. Penck on a scale of 1:1,000,000, which has been undertaken by the leading governments of the world, the ground is shown by contours at intervals of 100 metres (to be increased to 200 and 500 metres in mountainous districts); the strata are in graded tints, viz. blue for the sea, green for lowlands up to 300 metres, yellow between 300 and 500 metres, brown up to 2000 metres, and reddish tints beyond that height.
The declivities of the ground are still indicated in most topographical maps by a system of strokes or hachures, first devised by L. Chr. Müller (Plan und Kartenzeichnen, 1788) and J. G. Lehmann, who directed a survey of Saxony, 1780–1806, and published his Theorie der Bergzeichnung in 1799. By this method the slopes are indicated by strokes or hachures crossing the contour lines at right angles, in the direction of flowing water, and varying in thickness according to the degree of declivity they represent (cf. for example, the map of Switzerland in this work). The light is supposed to descend vertically upon the country represented, and in a true scale of shade the intensity increases with the inclination from 0° to 90°; but as such a scale does not sufficiently differentiate the lesser inclinations which are the most important, the author adopted a conventional scale, representing a slope of 45° or more, supposed to be inaccessible, as absolutely black, the level surfaces, which reflect all the light which falls upon them, as perfectly white, and the intervening slopes by a proportion between black and white, as in fig. 2.
The main principles of this system have been maintained, but its details have been modified frequently to suit special cases. Thus the French survey commission of 1828 fixed the proportion of black to white at one and a half times the angle of slope; while in Austria, where steep mountains constitute an important feature, solid black has been reserved for a slope of 80°, the proportion of black to white varying from 80:0 (for 50°) to 8:72 (for 5°). On the map of Germany (1:100,000) a slope of 50° is shown in solid black while stippled hachures are used for gentle slopes up to 10°. Instead of shading lines following the greatest slopes, lines following the contours and varying in their thickness and in their intervals apart, according to the slope of the ground to be represented, may be employed. This method affords a ready and expeditious means of sketching the ground, if the draughtsman limits himself to characteristically indicating its features by what have been called “form lines.” This method can be recommended in the case of plotting the results of an explorer’s route, or in the case of countries of which we have no regular survey (cf. the map of Afghanistan in this work).Instead of supposing the light to fall vertically upon the surface it is often supposed to fall obliquely, generally at an angle of 45° from the upper left-hand corner. It is claimed for this method that it affords a means of giving a graphic representation of Alpine districts where other methods of shading fail. The Dufour map of Switzerland (1:100,000) is one of the finest examples of this style of hill-shading. For use in the field, however, and for scientific work, a contoured map like Siegfried’s atlas of Switzerland, or, in the case of hilly country, a map shaded on the assumption of a vertical light, will prove more useful than one of these, notwithstanding that truth to nature and artistic beauty are claimed on their behalf.
Instead of shading by lines, a like effect may be produced by mezzotint shading (cf. the map of Italy, or other maps, in this work, on a similar method), and if this be combined with contour lines very satisfactory results can be achieved. If this tint be printed in grey or brown, isohypses, in black or red, show distinctly above it. The same combination is possible if hills engraved in the ordinary manner are printed in colours, as is done in an edition of the 1-inch ordnance map, with contours in red and hills hachured in brown.
Efforts have been made of late years to improve the available methods of representing ground, especially in Switzerland, but the so-called stereoscopic or relief maps produced by F. Becker, X. Imfeld, Kümmerly, F. Leuzinger and other able cartographers, however admirable as works of art, do not, from the point of utility, supersede the combination of horizontal contours with shaded slopes, such as have been long in use. There seems to be even less chance for the combination of coloured strata and hachures proposed by K. Peucker, whose theoretical disquisitions on aerial perspective are of interest, but have not hitherto led to satisfactory practical results.[3]
The above remarks apply more particularly to topographic maps. In the case of general maps on a smaller scale, the orographic features must be generalized by a skilful draughtsman and artist. One of the best modern examples of this kind is Vogel’s map of Germany, on a scale of 1:500,000.
Selection of Names and Orthography.—The nomenclature or “lettering” of maps is a subject deserving special attention. Not only should the names be carefully selected with special reference to the objects which the map is intended to serve, and to prevent overcrowding by the introduction of names which can serve no useful object, but they should also be arranged in such a manner as to be read easily by a person consulting the map. It is an accepted rule now that the spelling of names in countries using the Roman alphabet should be retained, with such exceptions as have been familiarized by long usage. In such cases, however, the correct native form should be added within brackets, as Florence (Firenze), Leghorn (Livorno), Cologne (Cöln) and so on. At the same time these corrupted forms should be eliminated as far as possible. Names in languages not using the Roman alphabet, or having no written alphabet should be spelt phonetically, as pronounced on the spot. An elaborate universal alphabet, abounding in diacritical marks, has been devised for the purpose by Professor Lepsius, and various other systems have been adopted for Oriental languages, and by certain missionary societies, adapted to the languages in which they teach. The following simple rules, laid down by a Committee of the Royal Geographical Society, will be found sufficient as a rule; according to this system the vowels are to be sounded as in Italian, the consonants as in English, and no redundant letters are to be introduced. The diphthong ai is to be pronounced as in aisle; au as ow in how; aw as in law. Ch is always to be sounded as in church, g is always hard; y always represents a consonant; whilst kh and gh stand for gutturals. One accent only is to be used, the acute, to denote the syllable on which stress is laid. This system has in great measure been followed throughout the present work, but it is obvious that in numerous instances these rules must prove inadequate. The introduction of additional diacritical marks, such as ˉ and ˘, used to express quantity, and the diaeresis, as in aï, to express consecutive vowels, which are to be pronounced separately, may prove of service, as also such letters as ä, ö and ü, to be pronounced as in German, and in lieu of the French ai, eu or u.
The United States Geographic Board acts upon rules practically identical with those indicated, and compiles official lists of place-names, the use of which is binding upon government departments, but which it would hardly be wise to follow universally in the case of names of places outside America.
Measurement on Maps
Measurement of Distance.—The shortest distance between two places on the surface of a globe is represented by the arc of a great circle. If the two places are upon the same meridian or upon the equator the exact distance separating them is to be found by reference to a table giving the lengths of arcs of a meridian and of the equator. In all other cases recourse must be had to a map, a globe or mathematical formula. Measurements made on a topographical map yield the most satisfactory results. Even a general map may be trusted, as long as we keep within ten degrees of its centre. In the case of more considerable distances, however, a globe of suitable size should be consulted, or—and this seems preferable—they should be calculated by the rules of spherical trigonometry. The problem then resolves itself in the solution of a spherical triangle.
In the formulae which follow we suppose l and l ′ to represent the latitudes, a and b the co-latitudes (90°−l or 90°−l ′), and t the difference in longitude between them or the meridian distance, whilst D is the distance required.
If both places have the same latitude we have to deal with an isosceles triangle, of which two sides and the included angle are given. This triangle, for the convenience of calculation, we divide into two right-angled triangles. Then we have sin 12 D = sin a sin 12t, and since sin a = sin (90°−l) = cos t, it follows that
sin 12 D = cos l sin 12t.
If the latitudes differ, we have to solve an oblique-angled spherical triangle, of which two sides and the included angle are given. Thus,
cos t =cos D - cos a cos bsin a sin b
| cos D | = cos a cos b + sin a sin b cos t |
| = sin l sin l ′ + cos l cos l ′ cos t. |
In order to adapt this formula to logarithms, we introduce a subsidiary angle p, such that cot p = cot l cos t; we then have
In the above formulae our earth is assumed to be a sphere, but when calculating and reducing to the sea-level, a base-line, or the side of a primary triangulation, account must be taken of the spheroidal shape of the earth and of the elevation above the sea-level. The error due to the neglect of the former would at most amount to 1%, while a reduction to the mean level of the sea necessitates but a trifling reduction, amounting, in the case of a base-line 100,000 metres in length, measured on a plateau of 3700 metres (12,000 ft.) in height, to 57 metres only.
These orthodromic distances are of course shorter than those measured along a loxodromic line, which intersects all parallels at the same angle. Thus the distance between New York and Oporto, following the former (great circle sailing), amounts to 3000 m., while following the rhumb, as in Mercator sailing, it would amount to 3120 m.
These direct distances may of course differ widely with the distance which it is necessary to travel between two places along a road, down a winding river or a sinuous coast-line. Thus, the direct distance, as the crow flies, between Brig and the hospice of the Simplon amounts to 4.42 geogr. m. (slope nearly 9°), while the distance by road measures 13.85 geogr. m. (slope nearly 3°). Distances such as these can be measured only on a topographical map of a fairly large scale, for on general maps many of the details needed for that purpose can no longer be represented. Space runners for facilitating these measurements, variously known as chartometers, curvimeters, opisometers, &c., have been devised in great variety. Nearly all these instruments register the revolution of a small wheel of known circumference, which is run along the line to be measured.
The Measurement of Areas is easily effected if the map at our disposal is drawn on an equal area projection. In that case we need simply cover the map with a network of squares—the area of each of which has been determined with reference to the scale of the map—count the squares, and estimate the contents of those only partially enclosed within the boundary, and the result will give the area desired. Instead of drawing these squares upon the map itself, they may be engraved or etched upon glass, or drawn upon transparent celluloid or tracing-paper. Still more expeditious is the use of a planimeter, such as Captain Prytz’s “Hatchet Planimeter,” which yields fairly accurate results, or G. Coradi’s “Polar Planimeter,” one of the most trustworthy instruments of the kind.[4]
When dealing with maps not drawn on an equal area projection we substitute quadrilaterals bounded by meridians and parallels, the areas for which are given in the “Smithsonian Geographical Tables” (1894), in Professor H. Wagner’s tables in the geographical Jahrbuch, or similar works.
It is obvious that the area of a group of mountains projected on a horizontal plane, such as is presented by a map, must differ widely from the area of the superficies or physical surface of those mountains exposed to the air. Thus, a slope of 45° having a surface of 100 sq. m. projected upon a horizontal plane only measures 59 sq. m., whilst 100 sq. m. of the snowclad Sentis in Appenzell are reduced to 10 sq. m. A hypsographical map affords the readiest solution of this question. Given the area A of the plane between the two horizontal contours, the height h of the upper above the lower contour, the length of the upper contour l, and the area of the face presented by the edge of the upper stratum l.h = A1, the slope α is found to be tan α = h.l / (A − A1); hence its superficies, A = A2 sec α. The result is an approximation, for inequalities of the ground bounded by the two contours have not been considered.
The hypsographical map facilitates likewise the determination of the mean height of a country, and this height, combined with the area, the determination of volume, or cubic contents, is a simple matter.[5]
Relief Maps are intended to present a representation of the ground which shall be absolutely true to nature. The object, however, can be fully attained only if the scale of the map is sufficiently large, if the horizontal and vertical scales are identical, so that there shall be no exaggeration of the heights, and if regard is had, eventually, to the curvature of the earth’s surface. Relief maps on a small scale necessitate a generalization of the features of the ground, as in the case of ordinary maps, as likewise an exaggeration of the heights. Thus on a relief on a scale of 1:1,000,000 a mountain like Ben Nevis would only rise to a height of 1.3 mm.
The methods of producing reliefs vary according to the scale and the materials available. A simple plan is as follows—draw an outline of the country of which a map is to be produced upon a board; mark all points the altitude of which is known or can be estimated by pins or wires clipped off so as to denote the heights; mark river-courses and suitable profiles by strips of vellum and finally finish your model with the aid of a good map, in clay or wax. If contoured maps are available it is easy to build up a strata-relief, which facilitates the completion of the relief so that it shall be a fair representation of nature, which the strata-relief cannot claim to be. A pantograph armed with cutting-files[6] which carve the relief out of a block of gypsum, was employed in 1893–1900 by C. Perron of Geneva, in producing his relief map of Switzerland on a scale of 1:100,000. After copies of such reliefs have been taken in gypsum, cement, statuary pasteboard, fossil dust mixed with vegetable oil, or some other suitable material, they are painted. If a number of copies is required it may be advisable to print a map of the country represented in colours, and either to emboss this map, backed with papier-mâché, or paste it upon a copy of the relief—a task of some difficulty. Relief maps are frequently objected to on account of their cost, bulk and weight, but their great use in teaching geography is undeniable.
Globes.[7]—It is impossible to represent on a plane the whole of the earth’s surface, or even a large extent of it, without a considerable amount of distortion. On the other hand a map drawn on the surface of a sphere representing a terrestrial globe will prove true to nature, for it possesses, in combination, the qualities which the ingenuity of no mathematician has hitherto succeeded in imparting to a projection intended for a map of some extent, namely, equivalence of areas of distances and angles. Nevertheless, it should be observed that our globes take no account of the oblateness of our sphere; but as the difference in length between the circumference of the equator and the perimeter of a meridian ellipse only amounts to 0.16%, it could be shown only on a globe of unusual size.
The method of manufacturing a globe is much the same as it was at the beginning of the 16th century. A matrix of wood or iron is covered with successive layers of papers, pasted together so as to form pasteboard. The shell thus formed is then cut along the line of the intended equator into two hemispheres, they are then again glued together and made to revolve round an axis the ends of which passed through the poles and entered a metal meridian circle. The sphere is then coated with plaster or whiting, and when it has been smoothed on a lathe and dried, the lines representing meridians and parallels are drawn upon it. Finally the globe is covered with the paper gores upon which the map is drawn. The adaption of these gores to the curvature of the sphere calls for great care. Generally from 12 to 24 gores and two small segments for the polar regions printed on vellum paper are used for each globe. The method of preparing these gores was originally found empirically, but since the days of Albert Dürer it has also engaged the minds of many mathematicians, foremost among whom was Professor A. G. Kästner of Göttingen. One of the best instructions for the manufacture of globes we owe to Altmütter of Vienna.[8]
Larger globes are usually on a stand the top of which supports an artificial horizon. The globe itself rotates within a metallic meridian to which its axis is attached. Other accessories are an hour-circle, around the north pole, a compass placed beneath the globe, and a flexible quadrant used for finding the distances between places. These accessories are indispensable if it be proposed to solve the problems usually propounded in books on the “use of the globes,” but can be dispensed with if the globe is to serve only as a map of the world. The size of a globe is usually given in terms of its diameter. To find its scale divide the mean diameter of the earth (1,273,500 m.) by the diameter of the globe; to find its circumference multiply the diameter by π (3.1416).
Map Printing.—Maps were first printed in the second half of the 15th century. Those in the Rudimentum novitiarum published at Lübeck in 1475 are from woodcuts, while the maps in the first two editions of Ptolemy published in Italy in 1472 are from copper plates. Wood engraving kept its ground for a considerable period, especially in Germany, but copper in the end supplanted it, and owing to the beauty and clearness of the maps produced by a combination of engraving and etching it still maintains its ground. The objection that a copper plate shows signs of wear after a thousand impressions have been taken has been removed, since duplicate plates are readily produced by electrotyping, while transfers of copper engravings, on stone, zinc or aluminium, make it possible to turn out large editions in a printing-machine, which thus supersedes the slow-working hand-press.[9] These impressions from transfers, however, are liable to be inferior to impressions taken from an original plate or an electrotype. The art of lithography greatly affected the production of maps. The work is either engraved upon the stone (which yields the most satisfactory result at half the cost of copper-engraving), or it is drawn upon the stone by pen, brush or chalk (after the stone has been “grained”), or it is transferred from a drawing upon transfer paper in lithographic ink. In chromolithography a stone is required for each colour. Owing to the great weight of stones, their cost and their liability of being fractured in the press, zinc plates, and more recently aluminium plates, have largely taken the place of stone. The processes of zincography and of algraphy (aluminium printing) are essentially the same as lithography. Zincographs are generally used for producing surface blocks or plates which may be printed in the same way as a wood-cut. Another process of producing such blocks is known as cerography (Gr. κηρός), wax. A copper plate having been coated with wax, outline and ornament are cut into the wax, the lettering is impressed with type, and the intaglio thus produced is electrotyped.[10] Movable types are utilized in several other ways in the production of maps. Thus the lettering of the map, having been set up in type, is inked in and transferred to a stone or a zinc-plate, or it is impressed upon transfer-paper and transferred to the stone. Photographic processes have been utilized not only in reducing maps to a smaller scale, but also for producing stones and plates from which they may be printed. The manuscript maps intended to be produced by photographic processes upon stone, zinc or aluminium, are drawn on a scale somewhat larger than the scale on which they are to be printed, thus eliminating all those imperfections which are inherent in a pen-drawing. The saving in time and cost by adopting this process is considerable, for a plan, the engraving of which takes two years, can now be produced in two days. Another process, photo- or heliogravure, for obtaining an engraved image on a copper plate, was for the first time employed on a large scale for producing a new topographical map of the Austrian Empire in 718 sheets, on a scale of 1:75,000, which was completed in seventeen years (1873–1890). The original drawings for this map had to be done with exceptional neatness, the draughtsman spending twelve months on that which he would have completed in four months had it been intended to engrave the map on copper; yet an average chart, measuring 530 by 630 mm., which would have taken two years and nine months for drawing and engraving, was completed in less than fifteen months—fifty days of which were spent in “retouching” the copper plate. It only cost £169 as compared with £360 had the old method been pursued.
For details of the various methods of reproduction see Lithography; Process, &c.
History of Cartography
A capacity to understand the nature of maps is possessed even by peoples whom we are in the habit of describing as “savages.” Wandering tribes naturally enjoy a great advantage in this respect over sedentary ones. Our arctic voyagers—Sir E. W. Parry, Sir J. Ross, Sir F. L. MacClintock and others—have profited from rough maps drawn for them by Eskimos. Specimens of such maps are given in C. F. Hall’s Life with the Esquimaux (London, 1864). Henry Youle Hind, in his work on the Labrador Peninsula (London, 1863) praises the map which the Montagnais and Nasquapee Indians drew upon bark. Similar essays at map-making are reported in connexion with Australians, Maoris and Polynesians. Tupaya, a Tahitian, who accompanied Captain Cook in the “Endeavour” to Europe, supplied his patron with maps; Raraka drew a map in chalk of the Paumotu archipelago on the deck of Captain Wilkes’s vessel; the Marshall islanders, according to Captain Winkler (Marine Rundschau, Oct. 1893) possess maps upon which the bearings of the islands are indicated by small strokes. Far superior were the maps found among the semi-civilized Mexicans when the Spaniards first discovered and invaded their country. Among them were cadastral plans of villages, maps of the provinces of the empire of the Aztecs, of towns and of the coast. Montezuma presented Cortes with a map, painted on Nequen cloth, of the Gulf coast. Another map did the Conquistador good service on his campaign against Honduras (Lorenzana, Historia de nueva España, Mexico, 1770; W. H. Prescott, History of the Conquest of Mexico, New York, 1843). Peru, the empire of the Incas, had not only ordinary maps, but also maps in relief, for Pedro Sarmiento da Gamboa (History of the Incas, translated by A. R. Markham, 1907) tells us that the 9th Inca (who died in 1191) ordered such reliefs to be produced of certain localities in a district which he had recently conquered and intended to colonize. These were the first relief maps on record. It is possible that these primitive efforts of American Indians might have been further developed, but the Spanish conquest put a stop to all progress, and for a consecutive history of the map and map-making we must turn to the Old World, and trace this history from Egypt and Babylon, through Greece, to our own age.
The ancient Egyptians were famed as “geometers,” and as early as the days of Rameses II. (Sesostris of the Greeks, 1333–1300 B.C.) there had been made a cadastral survey of the country showing the rows of pillars which separated the nomens as well as the boundaries of landed estates. It was upon a map based upon such a source that Eratosthenes (276–196 B.C.) measured the distance between Syene and Alexandria which he required for his determination of the length of a degree. Ptolemy, who had access to the treasures of the famous library of Alexandria was able, no doubt, to utilize these cadastral plans when compiling his geography. It should be noted that he places Syene only two degrees to the east of Alexandria instead of three degrees, the actual meridian distance between the two places; a difference which would result from an error of only 7° is the orientation of the map used by Ptolemy. Scarcely any specimens of ancient Egyptian cartography have survived. In the Turin Museum are preserved two papyri with rough drawings of gold mines established by Sesostris in the Nubian Desert.[11] These drawings have been commented upon by S. Birch, F. Chabas, R. J. Lauth and other Egyptologists, and have been referred to as the two most ancient maps in existence. They can, however, hardly be described as maps, while in age they are surpassed by several cartographical clay tablets discovered in Babylonia. On another papyrus in the same museum is depicted the victorious return of Seti I. (1366–1333) from Syria, showing the road from Pelusium to Heroopolis, the canal from the Nile with crocodiles, and a lake (mod. Lake Timsah) with fish in it. Apollonius of Rhodes who succeeded Eratosthenes as chief librarian at Alexandria (196 B.C.) reports in his Argonautica (iv. 279) that the inhabitants of Colchis whom, like Herodotus (ii., 104) he looks upon as the descendants of Egyptian colonists, preserved, as heirlooms, certain graven tablets (κύρβεις) on which land and sea, roads and towns were accurately indicated.[12] Eustathius (since 1160 archbishop of Thessalonica) in his commentary on Dionysius Periegetes, mentions route-maps which Sesostris caused to be prepared, while Strabo (i., 1. 5) dwells at length upon the wealth of geographical documents to be found in the library of Alexandria.
A cadastral survey for purposes of taxation was already at work in Babylonia in the age of Sargon of Akkad, 3800 B.C. In the British Museum may be seen a series of clay tablets, circular in shape and dating back to 2300 or 2100 B.C., which contain surveys of lands. One of these depicts in a rough way lower Babylonia encircled by a “salt water river,” Oceanus.
Development of Map-making among the Greeks.[13]—Ionian mercenaries and traders first arrived in Egypt, on the invitation of Psammetichus I. about the middle of the 7th century B.C. Among the visitors to Egypt, there were, no doubt, some who took an interest in the science of the Egyptians. One of the most distinguished among them was Thales of Miletus (640–543 B.C.), the founder of the Ionian school of philosophy, whose pupil, Anaximander (611–546 B.C.) is credited by Eratosthenes with having designed the first map of the world. Anaximander looked upon the earth as a section of a cylinder, of considerable thickness, suspended in the centre of the circular vault of the heavens, an idea perhaps borrowed from the Babylonians, for Job (xxvi. 7) already speaks of the earth as “hanging upon nothing.” Like Homer he looked upon the habitable world (οἰκουμένη) as being circular in outline and bounded by a circumfluent river. The geographical knowledge of Anaximander was naturally more ample than that of Homer, for it extended from the Cassiterides or Tin Islands in the west to the Caspian in the east, which he conceived to open out into Oceanus. The Aegean Sea occupied the centre of the map, while the line where ocean and firmament seemed to meet represented an enlarged horizon.
Anaximenes, a pupil of Anaximander, was the first to reject the view that the earth was a circular plane, but held it to be an oblong rectangle, buoyed up in the midst of the heavens by the compressed air upon which it rested. Circular maps, however, remained in the popular favour long after their erroneousness had been recognized by the learned.
Even Hecataeus of Miletus (549–472 B.C.), the author of a Periodos or description of the earth, of whom Herodotus borrowed the terse saying that Egypt was the gift of the Nile, retained this circular shape and circumfluent ocean when producing his map of the world, although he had at his disposal the results of the voyage of Scylax of Caryanda from the Indus to the Red Sea, of Darius’ campaign in Scythia (513), the information to be gathered among the merchants from all parts of the world who frequented an emporium like Miletus, and what he had learned in the course of his own extensive travels. Hecataeus was probably the author of the “bronze tablets upon which was engraved the whole circuit of the earth, the sea and rivers” (Herod, v. 49), which Aristagoras, the tyrant of Miletus, showed to Cleomenes, the king of Sparta, in 504, whose aid he sought in vain in a proposed revolt against Darius, which resulted disastrously in 494 in the destruction of Miletus. The map of the world brought upon the stage in Aristophanes’ comedy of The Clouds (423 B.C.), whereon a disciple of the Sophists points out upon it the position of Athens and of other places known to the audience, was probably of the popular circular type, which Herodotus (iv. 36) not many years before had derided and which was discarded by Greek cartographers ever after. Thus Democritus of Abdera (b. c. 450, d. after 360), the great philosopher and founder, with Leucippus, of the atomic theory, was also the author of a map of the inhabited world which he supposed to be half as long again from west to east, as it was broad.
Dicaearcus of Messana in Sicily, a pupil of Aristotle (326–296 B.C.), is the author of a topographical account of Hellas, with maps, of which only fragments are preserved; he is credited with having estimated the size of the earth, and, as far as known he was the first to draw a parallel across a map.[14] This parallel, or dividing line, called diaphragm (partition) by a commentator, extended due east from the Pillars of Hercules, through the Mediterranean, and along the Taurus and Imaus (Himalaya) to the eastern ocean. It divided the inhabited world, as then known, into a northern and a southern half. In compiling his map he was able to avail himself of the information obtained by the bematists (surveyors who determined distances by pacing) who accompanied Alexander the Great on his campaigns; of the results of the voyage of Nearchus from the Indus to the Euphrates, and of the “Periplus” of Scylax of Caryanda, which described the coast from between India and the head of the Arabian Gulf. On the other hand he unwisely rejected the results of the observations for latitude made by Pytheas in 326 B.C. at his native town, Massilia, and during a subsequent voyage to northern Europe. In the end the map of Dicaearcus resembled that of Democritus.
Scientific geography profited largely from the labours of Eratosthenes of Cyrene, whom Ptolemy Euergetes appointed keeper of the famous library of Alexandria in 247 B.C., and died in that city in 195 B.C. He won fame as having been the first to determine the size of the earth by a scientific method. Having determined the difference of latitude between Alexandria and Syene which he erroneously believed to lie on the same meridian, and obtained the distance of those places from each other from the surveys made by Egyptian geometers, he concluded that a degree of the meridian measured 700 stadia.[15]
Eratosthenes is the author of a treatise which deals systematically with the geographical knowledge of his time, but of which only fragments have been preserved by Strabo and others. This treatise was intended to illustrate and explain his map of the world. In this task he was much helped by the materials collected in his library. Among the travellers of whose information he was thus able to avail himself were Pytheas of Massilia, Patroclus, who had visited the Caspian (285–282 B.C.), Megasthenes, who visited Palibothra on the Ganges, as ambassador of Seleucus Nicator (302–291 B.C.), Timosthenus of Rhodes, the commander of the fleet of Ptolemy Philadelphus (284–246 B.C.) who wrote a treatise “On harbours,” and Philo, who visited Meroe on the upper Nile. His map formed a parallelogram measuring 75,800 stadia from Usisama (Ushant island) or Sacrum Promontorium in the west to the mouth of the Ganges and the land of the Coniaci (Comorin) in the east, and 46,000 stadia from Thule in the north to the supposed southern limit of Libya. Across it were drawn seven parallels, running through Meroe, Syene, Alexandria, Rhodes, Lysimachia on the Hellespont, the mouth of the Borysthenes and Thule, and these were crossed at right angles by seven meridians, drawn at irregular intervals, and passing through the Pillars of Hercules, Carthage, Alexandria, Thapsacus on the Euphrates, the Caspian gates, the mouth of the Indus and that of the Ganges. The position of all the places mentioned was supposed to have been determined by trustworthy authorities. The inhabited world thus delineated formed an island of irregular shape, surrounded on all sides by the ocean, the Erythrean Sea freely communicating with the western ocean. In his text Eratosthenes ignored the popular division of the world into Europe, Asia and Libya, and substituted for it a northern and southern division, divided by the parallel of Rhodes, each of which he subdivided into sphragides or plinthia—seals or plinths. The principles on which these divisions were made remain an enigma to the present day.
This map of Eratosthenes, notwithstanding its many errors, such as the assumed connexion of the Caspian with a northern ocean and the supposition that Carthage, Sicily and Rome lay on the same meridian, enjoyed a high reputation in his day. Even Strabo (c. 30 B.C.) adopted its main features, but while he improved the European frontier, he rejected the valuable information secured by Pytheas and retained the connexion between the Caspian and the outer ocean. In the extreme east his information extended no further than that of Eratosthenes, viz. to India and Taprobane (Ceylon) and the Sacae (Kirghiz).
Hipparchus, the famous astronomer, on the other hand, (c. 150 B.C.) proved a somewhat captious critic. He justly objected to the arbitrary network of the map of Eratosthenes. The parallels or climata[16] drawn through places, of which the longest day is of equal length and the decimation (distance) from the equator is the same, he maintained, ought to have been inserted at equal intervals, say of half an hour, and the meridians inserted on a like principle. In fact, he demanded that maps should be based upon a regular projection, several descriptions of which he had adopted for his star maps. He moreover accuses Eratosthenes, (whose determination of a degree he accepts without hesitation) with trusting too much to hypothesis in compiling his map instead of having recourse to latitudes and longitudes deduced by astronomical observations. Such observations, however, were but rarely available at the time. A few latitudes had indeed been observed, but although Hipparchus had shown how longitudes could be determined by the observation of eclipses, this method was in reality not available for want of trustworthy time-keepers. The determination of an ocean surrounding the inhabited earth he declared to be based on a mere hypothesis and that it would be equally allowable to describe the Erythraea as a sea surrounded by land. Hipparchus is not known to have compiled a map himself.
About the same time Crates of Mallus (d. 145 B.C.) embodied the views of the Stoic school of philosophy in a globe which has become typical as one of the insignia of royalty. On this globe an equatorial and a meridional ocean divide our earth into four quarters, each inhabited, thus anticipating the discovery of North and South America and Australia.[17]
The period between Eratosthenes and Marinus of Tyre was one of great political importance. Carthage had been destroyed (146 B.C.), Julius Caesar had carried on his campaign in Gaul (58–51 B.C.), Egypt had been occupied (30 B.C.), Britannia conquered (A.D. 41–79), and the Roman empire had attained its greatest extent and power under the emperor Trajan (A.D. 98–117). But although military operations added to our knowledge of the world, scientific cartography was utterly neglected.
Among Greek works written during this period there are several which either give us an idea of the maps available at that time, or furnish information of direct service to the compiler of a map. Among the latter a Periplus or coastal guide of the Erythrean Sea, which clearly reveals the peninsular shape of India (A.D. 90) and Arrian’s Periplus Ponti Euxeni (A.D. 131) which Festus Avienus translated into Latin. Among travellers Eudoxus of Cyzicus occupies a foremost rank, since, between 115–87 B.C. he visited India and the east coast of Africa, which subsequently he attempted in vain to circumnavigate by following the route of Hanno, along the west coast. Among geographers should be mentioned Posidonius (135–51), the head of the Stoic school of Rhodes, who is stated to be responsible for having reduced the length of a degree to 500 stadia; Artemidorus of Ephesus, whose “Geographumena” (c. 100 B.C.) are based upon his own travels and a study of itineraries, and above all, Strabo, who has already been referred to. Among historians who looked upon geography as an important aid in their work are numbered Polybius (c. 210–120 B.C.), Diodorus Siculus (c. 30 B.C.) and Agathachidus of Cnidus (c. 120 B.C.) to whom we are indebted for a valuable account of the Erythrean Sea and the adjoining parts of Arabia and Ethiopia. The Periegesis of Dionysius of Alexandria is a popular description of the world in hexameters, of no particular scientific value (c. A.D. 130). He as well as Artemidorus and others accepted a circular or ellipsoidal shape of the world and a circumfluent ocean; Strabo alone adhered to the scientific theories of Eratosthenes.
The credit of having returned to the scientific principles innovated by Eratosthenes and Hipparchus is due to Marinus of Tyre (c. A.D. 120) which, though no longer occupying the pre-eminent position of former times, was yet an emporium of no inconsiderable importance, having extensive connexions by sea and land. The map of Marinus and the descriptive accounts which accompanied it have perished, but we learn sufficient concerning them from Ptolemy to be able to appreciate their merits and demerits. Marinus was the first who laid down the position of places on a projection according to their latitude and longitude, but the projection used by him was of the rudest. Parallels and meridians were represented by straight lines intersecting each other at right angles, the relative proportions between degrees of longitude and latitude being retained only along the parallel of Rhodes. The distortion of the countries represented would thus increase with the distance, north and south, from this central parallel. The number of places whose position had been determined by astronomical observation was as yet very small, and the map had thus to be compiled mainly from itineraries furnished by travellers or the dead reckoning of seamen. The errors due to an exaggeration of distances were still further increased on account of his assuming a degree to be equal to 500 stadia, as determined by Posidonius, instead of accepting the 700 stadia of Eratosthenes. He was thus led to assume that the distance from the first meridian drawn through the Fortunate islands to Sera (mod. Si-ngan-fu), the capital of China, was equal to 225°, which Ptolemy reduced to 177°, but which in reality only amount to 126°. A like overestimate of the distances covering the march of Julius Maternus to Agisymba, which Marinus places 24° south of the equator, a latitude which Ptolemy reduces to 18°, but which is probably no farther south than lat. 12° N. The map of Marinus was accompanied by a list of places arranged according to latitude and longitude. It must have been much in demand, for three editions of it were prepared. Masudi (10th century) saw a copy of it and declared it to be superior to Ptolemy’s map.
Ptolemy (q.v.) was the author of a Geography[18] (c. A.D. 150) in eight books. “Geography,” in the sense in which he uses the term, signifies the delineation of the known world, in the shape of a map, while chorography carries out the same objects in fuller detail, with regard to a particular country. In Book I. he deals with the principles of mathematical geography, map projections, and sources of information with special reference to his predecessor Marinus.
Books II. to VII. form an index to the maps. They contain about 8000 names, with their latitudes and longitudes, and with their aid it is possible to reconstruct the maps. These maps existed, as a matter of course, before such an index could be compiled, but it is doubtful whether the maps in our available manuscript, which are attributed to Agathodaemon, are copies of Ptolemy’s originals or have been compiled, after their loss, from this index. Book VIII. gives further details with reference to the principal towns of each map, as to geographical position, length of day, climata, &c.Ptolemy’s great merit consists in having accepted the views of Hipparchus with respect to a projection suited for a map of the world. Of the two projections proposed by him one is a modified conical projection with curved parallels and straight meridians; in the second projection (see fig. 3) both parallels and meridians are curved. The correct relations in the length of degrees of latitude and longitude are maintained in the first case along the latitude of Thule and the equator, in the second along the parallel of Agisymba, the equator and the parallels of Meroe, Syene and Thule. Following Hipparchus he divided the equator into 360° drawing his prime meridian through the Fortunate Islands (Canaries). The 26 special maps are drawn on a rectangular projection. As a map compiler Ptolemy does not take a high rank. In the main he copied Marinus whose work he revised and supplemented in some points, but he failed to realize the peninsular shape of India, erroneously exaggerated the size of Taprobane (Ceylon), and suggested that the Indian Ocean had no connexion with the western ocean, but formed Mare Clausum. Ptolemy knew but of a few latitudes which had been determined by actual observation, while of three longitudes resulting from simultaneous observation of eclipses he unfortunately accepted the least satisfactory, namely, that which placed Arbela 45° to the east of Carthage, while the actual meridian distance only amounts to 34°. An even graver source of error was Ptolemy’s acceptance of a degree of 500 instead of 700 stadia. The extent to which the more correct proportion would have affected the delineation of the Mediterranean is illustrated by fig. 4. But in spite of his errors the scientific method pursued by Ptolemy was correct, and though he was neglected by the Romans and during the middle ages, once he had become known, in the 15th century, he became the teacher of the modern world.
Map-Making among the Romans.—We learn from Cicero, Vitruvius, Seneca, Suetonius, Pliny and others, that the Romans had both general and topographical maps. Thus, Varro (De rustici) mentions a map of Italy engraved on marble, in the temple of Tellus, Pliny, a map of the seat of war in Armenia, of the time of the emperor Nero, and the more famous map of the Roman Empire which was ordered to be prepared for Julius Caesar (44 b.c.), but only completed in the reign of Augustus, who placed a copy of it, engraved in marble, in the Porticus of his sister Octavia (7 b.c.). M. Vipsanius Agrippa, the son-in-law of Augustus (d. 12 b.c.), who superintended the completion of this famous map, also wrote a commentary illustrating it, quotations from which of Ammianus Marcellinus of Antioch (d. 330), Pliny and others, afford the only means of judging of its character. The map is supposed to be based upon actual surveys or rather reconnaissances, and if it be borne in mind that the Roman Empire at that time was traversed in all directions by roads furnished with mile-stones, that the Agrimensores employed upon such a duty were skilled surveyors, and that the official reports of the commanders of military expeditions and of provincial governors were available, this map, as well as the provincial maps upon which it was based, must have been a work of superior excellence, the loss of which is much to be regretted. A copy of it may possibly have been utilized by Marinus and Ptolemy in their compilations. The Romans have been reproached for having neglected the scientific methods of map-making advocated by Hipparchus. Their maps, however, seem to have met the practical requirements of political administration and of military undertakings.
Only two specimens of Roman cartography have come down to us, viz. parts of a plan of Rome, of the time of the emperor Septimius Severus (a.d. 193–211), now in the Museo Capitolino, and an itinerarium scriptum, or road map of the world, compressed within a strip 745 mm. in length and 34 mm. broad. Of its character the reduced copy of one of its 12 sections (fig. 5) conveys an idea. The map, apparently of the 3rd century, was copied by a monk at Colmar, in 1265, who fortunately contented himself with adding a few scriptural names, and having been acquired by the learned Conrad Peutinger of

Fig. 5.—A Section of Peutinger's Tabula.
Map-Making in the Middle Ages.—In scientific matters the early middle ages were marked by stagnation and retrogression. The fathers of the church did not encourage scientific pursuits, which Lactantius (4th century) declared to be unprofitable. The doctrine of the sphericity of the earth was still held by the more learned, but the heads of the church held it to be unscriptural. Pope Zachary, when in 741 he condemned the views of Virgilius, the learned bishop of Salzburg, an Irishman who had been denounced as a heretic by St Boniface, declares it to be perversa et iniqua doctrina. Even after Gerbert of Aurillac, better known as Pope Sylvester II. (999–1063), Adam of Bremen (1075), Albertus Magnus (d. 1286), Roger Bacon (d. 1294), and indeed all men of leading had accepted as a fact and not a mere hypothesis the geocentric system of the universe and sphericity of the globe, the authors of maps of the world, nearly all of whom were monks, still looked in the main to the Holy Scriptures for guidance in outlining the inhabited world. We have to deal thus with three types of these early maps, viz. an oblong rectangular, a circular and an oval type, the latter being either
a compromise between the two former, or an artistic development of the circular type. In every instance the inhabited world is surrounded by the ocean. The authors of rectangular maps look upon the Tabernacle as an image of the world at large, and believe that such expressions as the “four corners of the earth” (Isa. x. 12), could be reconciled only with a rectangular world. On the other hand there was the expression “circuit of the earth” (Isa. xl. 22), and the statement (Ezek. v. 5) that “God had set Jerusalem in the midst of the nations and countries.” In nearly every case the East occupies the top of the map. Neither parallels nor meridians are indicated, nor is there a scale. Other features frequently met with are the Paradise in the Far East, miniatures of towns, plants, animals, human beings and monsters, and an indication of the twelve winds around the margin.The oldest rectangular map of the world is contained in a most valuable work written by Cosmas, an Alexandrian monk, surnamed Indicopleustes, after returning from a voyage to India (535 A.D.), and entitled Christian Topography. According to Cosmas (fig. 6) the inhabited earth has the shape of an oblong rectangle surrounded by an ocean which breaks in in four great gulfs—the Roman or Mediterranean, the Arabian, Persian and Caspian Sea. Beyond this ocean lies another world, which was occupied by man before the Deluge, and within which Cosmas placed the Terrestrial Paradise. Above this rise the walls of the heavens like unto the tent of the Tabernacle. Far more simple is a small map of the world of the 8th century found in a codex in the library of Albi, an archiepiscopal seat in the department of Tarn. Its scanty nomenclature is almost wholly derived from the “Historiae adversum paganos” of Paulus Orosius (418). Far greater interest attaches to the so-called Anglo-Saxon Map of the World in the British Museum (Cotton MSS.), where it is bound up in a codex which also contains a copy of the Periegesis of Priscianus. Map and Periegesis are copies by the same hand, but no other connexion exists between them. More than half the nomenclature of the map is derived from Orosius, an annotated Anglo-Saxon version of which had been produced by King Alfred (871–901). The Anglo-Saxons of the time were of course well acquainted with Island (first thus named in 870) Slesvic and Norweci (Norway), and there is no need to have recourse to Adam of Bremen (1076) to account for their presence upon this map. The broad features of the map were derived no doubt from an older document which may likewise have served as the basis for the map of the world engraved on silver for Charlemagne, and was also consulted by the compilers of the Hereford and Ebstorf maps (see fig. 11).

Fig. 9.—T map from Isidor of Seville’s Origines.
The map or diagram of which Leonardo Dati in his poem on the Sphere (Della Spera) wrote in 1422 “un T dentre a uno O mostra il disegno” (a T within an O shows the design) is one of the most persistent types among the circular or wheel maps of the world. It perpetuates the tripartite division of the world by the ancient Greeks and survives in the Royal Orb. A diagram of this description will be found in Isidor of Seville’s Origines (630), see fig. 9.
T maps of more elaborate design illustrate the MS. copies of Sallust’s Bellum jugurthinum; one of these taken from a codex of the 11th century in the Leipzig town library is shown in fig. 10.
The outlines of several medieval maps resemble each other to such an extent that there can be no doubt that they are derived from the same original source. This source by some
authors is assumed to have been the official map of the Roman Empire, but if we compare the crude outline given to the Mediterranean with the more correct delineation of Ptolemy, who was certainly in a position to avail himself of these official sources, such an assumption is untenable. The earliest delineation of the description has already been referred to as the Anglo-Saxon map of the world. Next in the order of age, follows the oval map which Henry, canon of Mayence Cathedral, dedicated to Mathilda, consort of the emperor Henry V. (1110). Of far greater importance is the map seen in Hereford Cathedral. It is the work of Richard of Haldingham, and has a diameter of 134 cm. (53 ins.). The “survey” ordered by Julius Caesar is referred to in the legend, evidently derived from the Cosmography of Aethicus a work widely read at the time, but this does not provethat the author was able to avail himself of a map based upon that survey. A map essentially identical with that of Hereford, but larger—its diameter is 15.6 cm. (6 in.), and consequently fuller of information—was discovered in 1830 in the old monastery of Ebstorf in Hanover. Its date is 1484. Both maps abound in miniature pictures of towns, animals, fabulous beings and other subjects. The Hereford map is surmounted by a picture of the Day of Judgment. Similar in design, though much smaller of scale and oval in form, are the maps which illustrate the popular Polychronicon of Ranulf Higden, a monk of St Werburgh’s Abbey of Chester (d. 1363).

Fig. 11.—The Hereford Map (c. 1280).
Pomponius Mela tells us that beyond the Ethiopian Ocean which sweeps round Africa in the south and the uninhabitable torrid zone, there lies an alter orbis, or fourth part of the world inhabited by Antichthones. On a diagram illustrating the origines of Isidore of Seville (d. 636) this country is shown, but is described as a terra inhabitabilis. It is shown likewise upon a number of maps which illustrate the Commentaries on the Apocalypse, by Beatus, a Benedictine monk of the abbey of Valcavado at the foot of the hills of Liebana in Asturia (776). Our little map (fig. 12) is taken from a copy of Beatus’ work made in 1203, and preserved at Burgo de Osma in Castille. Similar maps illustrating the Commentaries exist at St Sever (1050), Paris (1203), and Tunis; others are rectangular, the oldest being in Lord Ashburnham’s library (970). Beatus, too, describes the southern land as inhabitabilis. The habitable world is divided among the twelve apostles, whose portraits are given. On the maps illustrating the encyclopaedic Liber floridus by Lambert, a canon of St Omer (1120), this south land “unknown to the sons of Adam,” is stated to be inhabited “according to the philosophers” by Antipodes. Lambert, indeed, seems to have believed in the sphericity of the earth. Fig. 13 shows his map of the world reduced from a MS. at Wolfenbüttel, to which is added a diagram of the zones from a MS. at Ghent, which illustrates Macrobius’ commentary on Cicero’s Somnium Scipionis. Diagrams illustrating the division of the world into climata, are to be found in the opus majus of Roger Bacon (d. 1294) and in Cardinal Pierre d’Ailly’s De imagine Mundi (1410).
Among countries represented on a larger scale on maps, Palestine not unnaturally occupies a prominent place in this age of pilgrimages and crusades (1095–1291). The maps which accompany St Jerome’s translation of the Onomasticon of St Eusebius (388). The same subject is illustrated by a picture-map in mosaic, portions of which were discovered in 1896 on the floor of the church of Madaba to the east of the Dead Sea. This is the oldest original of a map in existence, for it dates back to the 6th century. Among more recent maps of Palestine, that by Petrus Vesconte (1320) is greatly superior to the earlier maps. It illustrates Marino Sanuto’s Secreta fidelium crucis, in which its author vainly appeals to Christendom to undertake another crusade. One of the earliest plans of Jerusalem is contained in Gesta Francorum, a history of the Crusades up to 1106, based upon information furnished by Fulcherius of Chartres (c. 1109).

Fig. 14.—Matthew of Paris
(1236–1259).
There existed, no doubt, special maps of European countries, but the only documents of that description are two maps of Great Britain, the one of the 12th century, the other by Matthew of Paris, the famous historiographer of the monastery of St Albans (1236–1259).[20]
Celestial globes were known in the time of Bede; they formed part of the educational apparatus of the monastic schools. Gerbert of Aurillac is known to have made such globes (929). Their manufacture is described by Alphonso the Wise (1252), as also in De sphaera solida of G. Campanus of Novara (1303). Terrestrial globes, however, are not referred to.
Map-making among the Arabians and other Nations of the East.—Bagdad early became a famous seat of learning. Indian astronomers found apt pupils there among the Arabs; the works of Ptolemy were translated into Arabic, and in 827, in the reign of the caliph Abdullah al Mamun, an arc of the meridian was measured in the plain of Mesopotamia. Most famous among these Arabian astronomers were Al Batani (d. 998), Ibn Yunis of Cairo (d. 1008), Zarkala (Azarchel), who determined the meridian distance between his observatory in Toledo and Bagdad to amount to 51° 30′, an error of 3° only, as compared with Ptolemy’s error of 18°, and Abul Hassan (1230) who reduced the great axis of the Mediterranean to 44°.
Further materials serviceable to the compilers of maps were supplied by numerous Arabian travellers and geographers, among whom Masudi (915–940), Istakhri (950), Ibn Haukal (942–970), Al Biruni (d. 1038), Ibn Batuta (1325–1356) and Abul Feda (1331–1370), occupy a foremost place, yet the few maps which have reached us are crude in the extreme. Masudi, who saw the maps in the Horismos or Rasm el Ard, a description of the world by Abu Jafar Mahommed ben Musa of Khiva, the librarian of the caliph el Mamun (833), declares them to be superior to the maps of Ptolemy or Marinus, but maps of a later date by Istakhri (950) or Ibn al Wardi (1349) are certainly of a most rudimentary type. Nor can Idrisi’s map of the world, which was engraved for King Roger of Sicily upon a silver plate, or the rectangular map in 70 sheets which accompanies his geography (Nushat-ul Mushtat) take rank with Ptolemy’s work. These maps are based upon information collected during many years at the instance of King Roger. The seven climates adopted by Idrisi are erroneously supposed to be equal in latitudinal extent. The Mediterranean occupies nearly half the inhabited world in longitude, and the east coast of Africa is shown as if it extended due east.
The Arabians are not known to have produced a terrestrial globe, but several of their celestial globes are to be found in our collections. The oldest of these globes was made at Valentia, and is now in the museum of Florence. Another globe (of 1225) is at Velletri; a third by Ibn Hula of Mosul (1275) is the property of the Royal Asiatic Society of London; a fourth (1289) from the observatory of Maragha, in the Dresden Museum, two globes of uncertain age at Paris (see fig. 17) and another in London. All these globes are of metal (bronze), or they might not have survived so many years.
The charts in use of the medieval navigators of the Indian Ocean—Arabs, Persians or Dravidas—were equal in value if not superior to the charts of the Mediterranean. Marco Polo mentions such charts; Vasco da Gama (1498) found them in the hands of his Indian pilot, and their nature is fully explained in the Mohit or encyclopaedia of the sea compiled from ancient sources by the Turkish admiral Sidi Ali Ben Hosein in 1554.[21] These charts are covered with a close network of lines intersecting each other at right angles. The horizontal lines are parallels, depending upon the altitude of the pole star, the Calves of the Little Bear and the Barrow of the Great Bear above the horizon. This altitude was expressed in isbas or inches each equivalent to 1° 42′ 50″. Each isba was divided into zams or eights. The interval between two parallels thus only amounted to 12′ 51″. These intervals were mistaken by the Portuguese occasionally for degrees, which account for Malacca, which is in lat. 2′ 13″ N., being placed on Cantino’s Chart (1502) in lat. 14′ S. It may have been a map of this kind which accounts for Ptolemy’s moderate exaggerations of the size of Taprobana (Ceylon). A first meridian, separating a leeward from a windward region, passed through Ras Kumhari (Comorin) and was thus nearly identical with the first meridian of the Indian astronomers which passed through the sacred city of Ujjain (Ozere of Ptolemy) or the meridian of Azin of the Arabs. Additional meridians were drawn at intervals of zams, supposed to be equal to three hours’ sail.
In China, maps in the olden time were engraved on bronze or stone, but after the 10th century they were printed from wood-blocks. Among the more important productions of more recent times, may be mentioned a map of the empire, said to be based upon actual surveys by Yhang (721), who also manufactured a celestial globe (an older globe by Ho-shing-tien, 4 metres in circumference, was produced in 450), and an atlas of the empire on a large scale by Thu-sie-pun (1311–1312) of which new enlarged editions with many maps were published in the 16th century and in 1799. None of these maps was graduated, which is all the more surprising as the Chinese astronomers are credited with having made use of the gnomon as early as 1000 B.C. for determining latitudes.
 |
| Fig. 17.—Globe in Bibliothèque Nationale, Paris |
 |
| Fig. 18.—The Indian Ocean according to Mohit, as interpreted by Dr Tomaschek. |
In the case of Japan, the earliest reference to a map is of 646, in which year the emperor ordered surveys of certain provinces to be made.
Portolano Maps.—During the long period of stagnation in cartography, which we have already dealt with, there survived among the seamen of the Mediterranean charts of remarkable accuracy, illustrating the Portolani or sailing directories in use among them. Charts of this description are first mentioned in connexion with the Crusade of Louis XI. in 1270, but they originated long before that time, and in the eastern part of the Mediterranean they embody materials available even in the days before Ptolemy, while the correct delineation of the west seems to be of a later date, and may have been due to Catalan seamen. These charts are based upon estimated bearings and distances between the principal ports or capes, the intervening coast-line being filled in from more detailed surveys. The bearings were dependent upon the seaman’s observation of the heavens, for these charts were in use long before the compass had been introduced on board ship (as early as 1205, according to Guiot de Provins) although it became fully serviceable only after the needle had been attached to the compass card, an improvement probably introduced by Flavio Gioja of Amalfi in the beginning of the 14th century. The compass may of course have been used for improving these charts, but they originated without its aid, and it is therefore misleading to describe them as Compass or Loxodromic charts, and they are now known as Portolano charts.
 |
| Fig. 19.—The Eastern Mediterranean, by Petrus Vesconte (1311). |
 |
| Fig. 20.—The Mediterranean. |
| a, According to A. Dulceti, 1339, and b, On Mercator’s projection, according to modern maps. |
None of these charts is graduated, and the horizontal and vertical lines which cross many of them represent neither parallels nor meridians. Their most characteristic feature, and one by which they can most readily be recognized, is presented by groups or systems of rhumb-lines, each group of these lines radiating from a common centre, the central group being generally encircled by eight or sixteen satellite groups. In the course of time the centres of radiation of all these groups had imposed upon them ornate rose dei venti, or windroses, such as may still be seen upon our compass-cards. Each chart was furnished with a scale of miles. These miles, however, were not the ordinary Roman miles of 1000 paces or 5000 ft., but smaller miles of Greek or Oriental origin, of which six were equal to five Roman miles, and as the latter were equal to 1480 metres, the Portolano miles had a length of only 1233 metres, and 75.2 of the former, and 90.3 of the latter were equal to a degree. The difference between these miles was known, however, only to the more learned among the map-makers, and when the charts were extended to the Atlantic seaboard the two were assumed to be identical.
 |
| Fig. 21.—Map illustrating Marino Sanuto’s Liber secretorum fidelium crucis. |
On these old charts the Mediterranean is delineated with surprising fidelity. The meridian distance between the Straits of Gibraltar and Beirut in Syria amounts upon them to about 3000 Portolano miles, equal in lat. 36° N. to 40.9°, as compared with an actual difference of 41.2°, and a difference of 61° assumed by Ptolemy. There exists, however, a serious error of orientation, due, according to Professor H. Wagner, to the inexperience of the cartographers who first combined the charts of the separate basins of the Mediterranean so as to produce a chart of the whole. This accounts for Gibraltar and Alexandria being shown as lying due east and west of each other, although there is a difference of 5° of latitude between them, a fact known long before Ptolemy.
The production of these charts employed numerous licensed draughtsmen in the principal seaports of Italy and Catalonia, and among seamen these MS. charts remained popular long after the productions of the printing-press had become available. The oldest of these maps which have been preserved, the so-called “Pisan chart,” which belongs probably to the middle of the 13th century, and a set of eight charts, known by the name of its former owner, the Cavaliere Tamar Luxoro, of somewhat later date, are both the work of Genoese artists. Among more eminent Genoese cartographers are Joannes da Carignano (d. 1344), Petrus Vesconte, who worked in 1311 and 1327, and is the draughtsman of the maps illustrating Marino Sanuto’s Liber secretorum fidelium crucis, which was to have roused Christendom to engage in another crusade (figs. 19 and 21) Battista Beccario (1426, 1435) and Bartolomeo Pareto (1455). Venice ranks next to Genoa as a centre of cartographic activity. Associated with it are Francesco Pizigano (1367–1373), Francesco de Cesanis (1421), Giacomo Giroldi (1422–1446), Andrea Bianco (1436–1448) Giovanni Leardo (1442–1452), Alvise Cadamosto, who was associated with the Portuguese explorers on the west coast of Africa (1454–1456) and whose Portolano was printed at Venice in 1490, and Fra Mauro (1457).
Associated with Ancona are Grazioso Benincasa and his son Andreas, whose numerous charts were produced between 1461 and 1508, and Count Ortomano Freducci (1497–1538).
 |
| Fig. 22.—Fra Mauro (1457). |
The earliest among Majorcan and Catalonian cartographers is Angelino Dulcert (1325–1339) whom A. Managhi claims as a Genoese, whose true name according to him was Angelino Dalorto. Other Catalans are Jahuda Cresques, a Jew of Barcelona, the supposed author of the famous Catalan map of the world (1375), Guglielmo Solerio (1384), Mecia de Viladestes (1413–1433) Gabriel de Valleseche (1439–1447) and Pietro Roselli, a pupil of Beccario of Genoa (1462).
These maps were originally intended for the use of seamen navigating the Mediterranean and the coasts of the Atlantic, but in the course of time they were extended to the mainland and ultimately developed into maps of the whole world as then known. Thus Pizigano’s map of 1367 extends as far east as the Gulf of Persia, whilst the Medicean map of 1356 (at Florence) is remarkable on account of a fairly correct delineation of the Caspian, the Shari river in Africa, and the correct direction given to the west coast of India, which had already been pointed out in a letter of the friar Giovanni da Montecorvino of 1252. Most of the expansions of Portolano maps into maps of the world are circular in shape, and resemble the wheel maps of an earlier period. This is the character of the map of Petrus Vesconte of 1320 (fig. 21), of Giovanni Leardo (1448) and of a Catalan map of 1450. Jerusalem occupies the centre of these maps, Arab sources of information are largely drawn upon, while Ptolemy is neglected and contemporary travellers are ignored. Far superior to these maps is Fra Mauro’s map (1457), for the author has availed himself not only of the information collected by Marco Polo and earlier travellers, but was able, by personal intercourse, to gather additional information from Nicolo de’ Conti, who had returned from the east in 1440, and more especially from Abyssinians who lived in Italy at that time. His delineation of Abyssinia, though unduly spread over a wide area, is indeed wonderfully correct.
 |
| Fig. 23.—Catalan Map of the World (1375). |
 |
| Fig. 24.—Genoese Map (1457). |
Very different in character is the Catalan map of 1375, for its author, discarding Ptolemy, shows India as a peninsula. On the other hand, an anonymous Genoese would-be reformer of maps (1457; fig. 24), still adheres to the erroneous Ptolemaic delineation of southern Asia, and the same error is perpetuated by Henricus Marvellus Germanus on a rough map showing the Portuguese discoveries up to 1489. None of these maps is graduated, but if we give the Mediterranean a length of 3000 Portolano miles, equivalent in 36° N. to 41°, then the longitudinal extent of the old world as measured on the Genoese map of 1457 would be 136° instead of 177° or more as given by Ptolemy.
 |
| Fig. 25.—Claudius Clavus Swartha (1427). |
The Revival of Ptolemy.—Ptolemy’s great work became known in western Europe after Jacobus Angelus de Scarparia had translated it into Latin in 1410. This version was first printed in 1475 at Vicenza, but its contents had become known through MS. copies before this, and their study influenced the construction of maps in two respects. They led firstly to the addition of degree lines to maps, and secondly to the compilation of new maps of those countries which had been inadequately represented by Ptolemy. Thus Claudius Clavus Swartha (Niger), who was at Rome in 1424, compiled a map of the world, extending westward as far as Greenland. The learned Cardinal Nicolaus Krebs, of Cusa (Cues) on the Moselle, who died 1464, drew a map of Germany which was first published in 1491; D. Nicolaus Germanus, a monk of Reichenbach, in 1466 prepared a set of Ptolemy’s maps on a new projection with converging meridians; and Paolo del Pozzo Toscanelli in 1474 compiled a new chart on a rectangular projection, which was to guide the explorer across the western ocean to Cathay and India.
Of the seven editions of Ptolemy which were published up to the close of the 15th century, all except that of Vicenza (1475) contained Ptolemy’s 27 maps, while Francesco Berlinghieri’s version (Florence 1478), and two editions published at Ulm (1482 and 1486), contained four or five modern maps in addition, those of Ulm being by Nicolaus Germanus.
The geographical ideas which prevailed at the time Columbus started in search of Cathay may be most readily gathered from two contemporary globes, the one known as the Laon globe because it was picked up in 1860 at a curiosity shop in that town, the other produced at Nuremberg in 1492 by Martin Behaim.[22] The Laon globe is of copper gilt, and has a diameter of 170 mm. The information which it furnishes, in spite of a legend intended to lead us to believe that it presents us with the results of Portuguese explorations up to the year 1493, is of more ancient date. The Nuremberg globe is a work of a more ambitious order. It was undertaken at the suggestion of George Holzschuher, a travelled member of the town council. The work was entrusted to Martin Behaim, who had resided for six years in Portugal and the Azores, and was believed to be a thoroughly qualified cosmographer. The globe is of pasteboard covered with whiting and parchment, and has a diameter of 507 mm. The author followed Ptolemy not only in Asia, but also in the Mediterranean. He did not avail himself of the materials available in his day. Not even the coasts of western Africa are laid down correctly, although the author claimed to have taken part in one of the Portuguese expeditions. The ocean separating Europe from Asia is assumed as being only 126° wide, in accordance with Toscanelli’s ideas of 1474. Very inadequate use has been made of the travels of Marco Polo, Nicolo de’ Conti, and of others in the east.[23] On the other hand, the globe is made gay with flags and other decorations, the work of George Glockendon, a well-known illuminator of the time.
 |
| Fig. 26. |
The maritime discoveries and surveys of that age of great discoveries were laid down upon so-called “plane-charts,” that is, charts having merely equidistant parallels indicated upon them, together with the equator, the tropics and polar circles, or, in a more advanced stage, meridians also. The astrolabe quadrant or cross-staff enabled the mariner to determine his latitude with a certain amount of accuracy, but for his longitude he was dependent upon dead reckoning, for although various methods for determining a longitude were known, the available astronomical ephemerides were not trustworthy, and errors of 30° in longitude were by no means rare. It was only after the publication of Kepler’s Rudolphine Table (1626) that more exact results could be obtained. A further difficulty arose in connexion with the variation of the compass, which induced Pedro Reinel to introduce two scales of latitude on his map of the northern Atlantic (1504; fig. 27).
 |
| Fig. 27. |
The chart of the world by Juan de la Cosa, the companion of Columbus, is the earliest extant which depicts the discoveries in the new world (1500), Nicolaus de Canerio, a Genoese, and the map which Alberto Cantino caused to be drawn at Lisbon for Hercules d’Este of Ferrara (1502), illustrating in addition the recent discoveries of the Portuguese in the East. Other cosmographers of distinction were Pedro Reinel (1504–1542), Nuno Garcia de Toreno (1520), to whom we are indebted for 21 charts, illustrating Magellan’s voyage, Diogo Ribero (maps of the world 1527, 1529),[24] Alonzo de Santa Cruz, of Seville, whose Isolario general includes charts of all parts of the world (1541), John Rotz or Rut (1542), Sebastian Cabot (1544), as also Nicolas Desliens, Pierre Desceliers, G. Breton and V. Vallard, all of Arques, near Dieppe, whose charts were compiled between 1541 and 1554.
Of the many general maps of the world or of particular countries, a large number illustrate such works as G. Reisch’s Margarita philosophica (1163), the cosmographies of Peter Apianus or Bienewitz (1520, 1522, 1530), Seb. Münster (1544), J. Honter (1546) and Gulielmus Postel (1561) or the Geographia of Livio Sanuto (1588); others, and these the more numerous and important, supplement the original maps of several editions of Ptolemy. Thus the Roman edition of 1507, edited by Marcus Benaventura and Joa Cota, contains 6 modern maps, and to these was added in 1508 Joh. Ruysch’s famous map of the world on a modified conical projection. The next edition published at Venice in 1511 contained a heart-shaped world by Bernhard Sylvanus. The Strassburg Ptolemy of 1513 has a supplement of as many as 20 modern maps by Martin Waldseemüller or Ilacomilus, several among which are copied from Portuguese originals. Waldseemüller was one of the most distinguished cartographers of his day. He was born at Radolfzell in Baden in 1470, was associated with Ringmann at the gymnasium of St Dié, and died in 1521. He published in 1507 a huge map of the world, in 12 sheets, together with a small globe of a diameter of 110 mm., the segments for which were printed from wood-blocks. On these documents the new world is called America, after Amerigo Vespucci, its supposed discoverer. In 1511 Waldseemüller published a large map of Europe, in 1513 he prepared his maps for the Strassburg edition of Ptolemy, and in 1516 he engraved a copy of Canerio’s map of the world. The Strassburg Ptolemy of 1522 contains Waldseemüller’s maps,[25] edited on a reduced scale by Laurentius Frisius, together with three additional ones. The same set of maps is reprinted in the Strassburg edition of 1524, newly translated by W. Pirckheimer with notes by Joh. Müller Regiomontanus, and in the Lyon edition of 1535, edited by Michael Servetus. The new maps of the Basel edition of 1540, twenty-one in number, are by Sebastian Münster; Jacob Gastaldo supplied the Venice edition of 1548 with 34 modern maps, and these with a few additions are repeated in Girolamo Ruscelli’s Italian translation of Ptolemy published at Venice in 1561.
Equally interesting with these Ptolemaic supplements are collections like that of Anton Lafreri, which contains reprints of 142 maps of all parts of the world originally published between 1556 and 1572 (Geografica tavole moderne, Rome, n.d.), or that of J. F. Camocio, published at Venice in 1576, which contains 88 reprints.
The number of cartographers throughout Europe was considerable, and we confine ourselves to mentioning a few leading men. Among them Germany is then represented by G. Glockedon, the author of an interesting road-map of central Europe (1501), Sebastian Münster (1489–1552), Elias Camerarius, whose map of the mark of Brandenburg won the praise of Mercator; Wolfgang Latz von Lazius, to whom we are indebted for maps of Austria and Hungary (1561), and Philip Apianus, who made a survey of Bavaria (1553–1563), which was published 1568 on the reduced scale of 1 : 144,000, and is fairly described as the topographical masterpiece of the 16th century. For maps of Switzerland we are indebted to Konrad Türst (1495–1497), Johann Stumpf (1548) and Aegidius Tschudi (1538). A map of the Netherlands from actual survey was produced by Jacob of Deventer (1536–1539). Leonardo da Vinci, the famous artist, while in the service of Cesare Borgia as military engineer, made surveys of several districts in central Italy. Other Italian cartographers of merit were Giovanni Battiste Agnese of Venice, whose atlases (1517–1564) enjoyed a wide popularity; Benedetto Bordone (1528); Giacomo Gastaldo, cosmographer of the Venetian Republic (1534–1568), and his successor, Paolo Forlani. New maps of Spain and Portugal appeared in 1560, the former being due to Pedro de Medina, the latter to Fernando Alvarez Secco and Hernando Alvaro. Among the French map-makers of this period may be mentioned Oronce Finée (Finaeus), who in 1525 published a map of France, and Jean Jolivet (c. 1560). Gregorio Lilly (1546) and Humphrey Lhuyd of Denbigh (d. 1510) furnished maps of the British Isles, Olaus Magnus (1539) of Scandinavia, Anton Wied (1542), Sigismund von Herberstein (1549) and Anthony Jenkinson (1562) of Muscovy.
The cylindrical and modified conical projections of Marinus and Ptolemy were still widely used, the stereographical projection of Hipparchus, was for the first time employed for terrestrial maps in the 16th century, but new projections were introduced in addition to these. The earliest of these, a trapeziform projection with equidistant parallels, by D. Nicolaus Germanus (1466), naturally led to what is generally known as Flamsteed’s projection. Joh. Stabius (1502) and his pupil J. Werner (1514) devised three heart-shaped projections, one of which was equivalent. Petrus Apianus (1524) gave his map an elliptical shape. H. Glareanus (1510) was the first to employ an equidistant zenithal polar projection.
No reasonable fault can be found with the marine surveyors of this period, but the scientific cartographers allowed themselves too frequently to be influenced by Ptolemaic traditions. Thus Gastaldo (1548) presents us with a map of Italy, which, except as to nomenclature, differs but little from that of Ptolemy, although on the Portolano charts the peninsula had long since assumed its correct shape. Many of the local maps, too, were excellent specimens of cartography, but when we follow any cartographer of the period into regions the successful delineation of which depended upon an intelligent interpretation of itineraries, and of information collected by recent travellers, they are generally found to fail utterly. This is illustrated by the four sketch maps shown in fig. 28.
 |
| Fig. 28. |
Columbus, trusting to Toscanelli’s misleading chart, looked upon the countries discovered by him as belonging to eastern Asia, a view still shared about 1507 by his brother Bartolomeo. Waldseemüller (1507) was the first to separate America and Asia by an ocean of considerable width, but J. Ruysch (1508) returns to the old idea, and even joins Greenland (Gruenlant) to eastern Asia. Bologninus Zalterius on a map of 1566, and Mercator on his famous chart of 1569, separates the two continents by a narrow strait which they call Streto de Anian, thus anticipating the discovery of Bering Strait by more than a hundred and fifty years. Anian, however, which they place upon the American coast, is no other than Marco Polo’s Anica or Anin, our modern Annam. Such an error could never have arisen had the old compilers of maps taken the trouble to plan Marco Polo’s routes.
Globes, both celestial and terrestrial, became popular after the discovery of America. They were included among the scientific apparatus of ships and of educational establishments. Columbus and Magellan had such globes, those of the latter produced by P. Reinel (1519), and Conrad Celtes tells us that he illustrated his lectures at the university of Vienna with the help of globes (1501). Globes were still engraved on copper, or painted by hand, but since 1507, in which year Waldseemüller published a small globe of a diameter of 110 mm., covered with printed segments or gores, this cheap and expeditious method has come into general use. Waldseemüller constructed his gores graphically, A. Dürer (1525) and Hen. Loriti Glareanus (1527) were the first who dealt scientifically with the principles underlying their construction. Globes covered with printed gores were produced by L. Boulenger (1514), Joh. Schöner (1515), P. Apianus, Gemma Frisius (1530) and G. Mercator (1541). Leonardo da Vinci’s rough map of the world in 8 segments (c. 1513) seems likewise to have been intended for a globe. Of J. Schöner we know that he produced four globes, three printed from segments (1515, 1523, 1533), and one of larger size (diam. 822 mm.), which is drawn by hand, and is preserved in the Germanic Museum at Nuremberg. Among engraved globes, one of the most interesting is that which was discovered by R. M. Hunt in Paris, and is preserved in the Lenox Library, New York. Its diameter is only 412 in. (127 mm.). The so-called “Nancy globe” is of chased silver, richly ornamented, and formerly served the purpose of a pyx. Its diameter is 160 mm., its date about 1530. About the same date is assigned to a globe by Robert de Bailly, engraved on copper and gilt (diam. 440 mm.). Celestial globes were manufactured by Regiomontanus (d. 1476) at Nuremberg, by Joh. Stöffler (1499), and by G. Hartmann (1535).
 |
| Fig. 29. |
 |
| Fig. 30.—Lenox Globes (1510). |
Mercator and his Successors.—Of Gerhard Kremer (1512–1594) the earliest works are a map of Palestine (1537), a map of the world on a double heart-shaped projection (1525), and a topographical map of Flanders based upon his own surveys (1540), a pair of globes (1541, diam. 120 mm.), and a large map of Europe which has been praised deservedly for its accuracy (1554). He is best known by his marine chart (1569) and his atlas. The projection of the former may have been suggested by a note by W. Pirkheimer in his edition of Ptolemy (1525). Mercator constructed it graphically, the mathematical principles underlying it being first explained by E. Wright (1594). The “Atlas” was only published after Mercator’s death, in 1595. It only contained nine maps, but after the plates had been sold to Jodocus (Jesse) Hondius the number of maps was rapidly increased, although Mercator’s name was retained. Mercator’s maps are carefully engraved on copper. Latin letters are used throughout; the miniatures of older maps are superseded by symbols, and in the better-known countries the maps are fairly correct, but they fail lamentably when we follow their author into regions—the successful delineation of which depends upon a critical combination of imperfect information.
Even before Mercator’s death, Antwerp and Amsterdam had become great centres of cartographic activity, and they maintained their pre-eminence until the beginning of the 18th century. Abraham Ortelius (1527–1592), of Antwerp, a man of culture and enterprise, but not a scientific cartographer, published the first edition of his Theatrum orbis terrarum in 1570. It then contained 53 maps, by various authors. By 1595 the number of maps had increased to 119, including a Parergon or supplement of 12 maps illustrating ancient history. In 1578 was published the Speculum orbis terrarum of Gerard de Jude or de Judaeis. Lucas Janszon Waghenaer (Aurigarius) of Enkhuizen published the first edition of his Spiegel der Zeevaart (Mariners’ Mirror) at Leiden in 1585. It was the first collection of marine maps, lived through many editions, was issued in several languages and became known as Charettier and Waggoner. In the same year Adrian Gerritsz published a valuable Paskaarte of the European Sea. Ten years afterwards, in 1595, W. Barentszoon published a marine atlas of the Mediterranean, the major axis of which he reduced to 42 degrees. Jodocus Hondius has already been referred to as the purchaser of Mercator’s plates. The business founded by him about 1602 was continued by his sons and his son-in-law, Jan Janszon (Jansonius) and others. By 1653 this firm had already produced atlases including 451 charts. Willem Janszon, the father of Hondius’s partner, published a collection of charts (1608), to which he gave the title of Het Licht der Zeevaart (the seaman’s light). Another cartographic publishing firm was established at Amsterdam in 1612 by Willem Janszon Blaeu (1571–1638), a friend of Tycho Brahe, from 1633 “mapmaker” of the states-general, and a man of scientific culture. He was succeeded by his son Jan (d. 1673) and grandson Cornelius, and before the end of the century turned out a Zee-Spiegel of 108 charts (1623), an Atlas novus (Nieuwe Atlas), 1642, enlarged in the course of time until it consisted of 12 folio volumes containing hundreds of maps. J. A. Colom in 1633 published a collection of maps under the quaint title of Vurig Colom der Zeevaert (Fiery Column of Navigation). Among more recent Dutch map publishers are Nicolaus Vischer (Piscator), R. Goos, H. Doncker, F. de Wit, and J. and G. van Keulen, whose atlases were published between 1681 and 1722. These Dutch maps and charts are generally accompanied by descriptive notes or sailing directions printed on the back of them. A similar work is the Arcano del mare of Sir Robert Dudley, duke of Northumberland, the numerous sheets of which are on Mercator’s projection (1631).
 |
| Fig. 31.—Mercator’s Chart of the World (1569). |
In France, in the meantime, an arc of the meridian had been measured (1669–1670) by Jean Picard, numerous longitudes had been observed between 1672 and 1680 by the same, and by Phil. de Lahire (d. 1719), and these were utilized in a Carte de France “as corrected from the observations of the members of the Academy of Sciences” (1666–1699), in a map of the world (1694) by D. Cassini, as also in Le Neptune François (1693) with contributions by Pene, D. Cassini and others. These corrected longitudes were not yet available for the maps produced by Nicolas Sanson of Abbeville, since 1627. The cartographical establishment founded by him in that year was carried on after his death in 1667 by his sons, his son-in-law, P. Duval (d. 1683) and his grandson Robert du Vaugondy (d. 1766). Among the cartographers whom he employed were M. Tavernier and Mariette, and in many instances he mentioned the authors whose maps he copied. By 1710 the maps published by the firm numbered 466. Nicolas de Fer, the great rival of Sanson, and his heirs, are stated to have published as many as 600 maps after 1700.
In no other country of Europe was there at the close of the 16th century a geographical establishment capable of competing with the Dutch towns or with Sanson, but the number of those who produced maps, in many instances based upon original surveys, was large. Germany is thus represented, among others, by C. Henneberger (map of Prussia, 1576), by M. Oeder, (survey of Saxony, 1586–1607), A. Rauh (fine hill features on a map of the environs of Wangen and Lindau, 1617), W. Schickhardt (survey of Württemberg, 1624–1635), and G. M. Vischer (map of Austria and Styrai, 1669–1786); Switzerland by H. C. Gyger (Canton of Zürich, a masterpiece, 1667); Italy by G. A. Magini (1558–1610), and V. Coronelli, appointed cosmographer of the Venetian Republic, 1685, and founder of the Ac. Cosmogr. dei Argonauti, the earliest geographical society, and Diogo Homem, a Portuguese settled at Venice (1558–1574); Denmark by J. Mejer of Husum (1650); Sweden by A. Buraeus, the “father of Swedish cartographers” (1650–1660); the British Islands by Ch. Saxton (County Atlas of England and Wales 1575), J. Speed (Theatrum of Great Britain, 1610), Timothy Pont and Robert Gordon of Strathloch (map of Scotland, 1608), and A. Moll. A Novus atlas sinensis, based upon Chinese surveys, was published in 1655 by Martin Martini, S.J., a missionary recently returned from China. Isaac Voss, in his work De Nili (1659), published a map of central Africa, in which he anticipated D’Anville by rejecting all the fanciful details which found a place upon Filippo Pigafetta’s map of that continent.
The first maps illustrating the variation of the compass were published by Chris. Burrus (d. 1632) and Athanasius Kircher (Magnes, Rome, 1643), and maps of the ocean and tidal currents by the latter in his Mundus subterraneus (1665). Edmund Halley, the astronomer, compiled the first variation chart of scientific value (1683), as also a chart of the winds (1686).
Globes manufactured for commercial purposes by Blaeu and others have already been mentioned, but several large globes, for show rather than for use, were produced in addition to these. Thus A. Busch, of Limburg (1656–1664), manufactured a globe for Duke Frederick of Holstein, formerly at Gottorp, but since 1713 at Tsarskoye Zelo. It has a diameter of 11 ft. (3.57 metres) and is hollow, the inner surface of the shell being covered with a star map, and the outer surface with a map of the world. Professor Erh. Weigel (1696) produced a hollow celestial globe in copper, having a small terrestrial globe in its centre. Its diameter is 3.25 metres. Lastly there is a pair of giant globes of artistic design, turned out by V. Coronelli (1623), and intended as presents to Louis XIV. Their diameter is nearly 5 metres. A pair of globes of 1592 by Emeric Molineux (diam. 610 mm.) is now in the Temple Library, and is referred to in Blundeville’s Exercises (1594).
The Eighteenth Century.—It was no mere accident which enabled France to enjoy a pre-eminence in cartographic work during the greater part of the 18th century. Not only had French men of science and scientific travellers done excellent work as explorers in different parts of the world, but France could also boast of two men, Guillaume Delisle and J. B. Bourguignon d’Anville, able to utilize in the compilation of their maps the information they acquired.
 |
| Fig. 32. |
Delisle (1675–1726) published 98 maps, and although as works of art they were inferior to the maps of certain contemporaries, they were far superior to them in scientific value. On one of his earliest maps compiled under advice of his father Claude (1700), he gave the Mediterranean its true longitudinal extension of 41°. It was Delisle who assumed the meridian of Ferro, which had been imposed upon French navigators by royal order (1634), to lie exactly 20° to the west of Paris. The work of reform was carried further by B. D’Anville (1697–1782). Altogether he published 211 maps, of which 66 are included in his Atlas général (1737–1780); he swept away the fanciful lakes from off the face of Africa, thus forcibly bringing home to us the poverty of our knowledge (fig. 32), delineated the Chinese Empire in accordance with the map based on the surveys conducted during the reign of the emperor Kanghi, with the aid of Jesuit missionaries, and published in 1718; boldly refused to believe in the existence of an Antarctic continent covering half the southern hemisphere, and always brought a sound judgment to bear upon the materials which the ever-increasing number of travellers placed at his disposal. Among other French works of importance deserving notice are Le Neptune oriental of Mannevillette (1745) and more especially the Carte géometrique de la France, which is based upon surveys carried on (1744–1783) by César François Cassini de Thury and his son Dominique de Cassini. It is on a transversal cylindrical (rectangular) projection devised by Jacques Cassini (d. 1746). The hills are shown in rough hachures.
England, which had entered upon a career of naval conquest and scientific exploration, had reason to be proud of J. F. W. Desbarres, Atlantic Neptune (1774), a North-American Pilot (1779), which first made known the naval surveys of J. Cook and of others; and Tho. Jefferys’s West Indian and American Atlases (1775, 1778). James Rennell (1742–1830), who was surveyor-general of India, published the Bengal Atlas (1781), and sagaciously arranged the vast mass of information collected by British travellers and others in India and Africa, but it is chiefly with the name of Aaron Arrowsmith, who came to London in 1778, and his successors, with which the glory of the older school of cartographers is most intimately connected. His nephew John died in 1873. Among local cartographers may be mentioned H. Moll (d. 1732), J. Senex, whose atlas was published in 1725, and Dowet, whose atlas was brought out at the expense of the duke of Argyll.
In Germany J. B. Homann (d. 1724) founded a geographical establishment in 1702, which depended at first upon copies of British and French maps, but in course of time published also original maps such as J. M. Hase’s Africa (1727) and Tobias Meyer’s Mappa critica of Germany (1780), J. T. Güssfeld’s map of Brandenburg (1773), John Majer’s Württemburg (1710), and J. C. Müller’s Bavaria, both based on trigonometrical surveys. Colonel Schmettau’s excellent survey of the country to the west of the Weser (1767–1787) was never published, as Frederick the Great feared it might prove of use to his military enemies. Switzerland is represented by J. J. Scheuchzer (1712), J. Gessner (d. 1790), G. Walser (Atlas novus Helvetiae, 1769), and W. R. Meyer, Atlas der Schweiz (1786–1802). Of the Austrian Netherlands, Count Joseph de Ferrari published a chorographic map on the same scale as Cassini’s Carte de la France (1777). Of Denmark a fine map was published under the auspices of the Academy of Science of Copenhagen (1766–1825); of Spain and Portugal an atlas in 102 sheets by Thomas Lopez (1765–1802); of Russia a map by J. N. Delisle in 19 sheets (1730–1745); charts illustrating the variation of the compass and of magnetic “dip” by E. Dunn (1776), J. C. Wiffe (1768); a chart of the world by W. Dampier (1789). Map projections were dealt with by two eminent mathematicians, J. H. Lambert (1772) and Leonh. Euler (1777).
On the maps of Delisle and d’Anville the ground is still represented by “molehills.” Hachures of a rude nature first made their appearance on David Vivier’s map of the environs of Paris (1674), and on Cassini’s Carte de la France. Contour lines (isobaths) were introduced for the first time on a chart of the Merwede by M. S. Cruquius (1728), and on a chart of the English Channel by Phil. Buache (1737). Dupain-Triel, acting on a suggestion of Du Carla, compiled a contoured map of France (1791), and it only needed the introduction of graduated tints between these contours to secure a graphic picture of the features of the ground. It was J. G. Lehmann (1783) who based his method of hill-shading or hachuring upon these horizontal contours. More than 80 methods of showing the hills have found advocates since that time, but all methods must be based upon contours to be scientifically satisfactory.
Two relief maps of Central Switzerland deserve to be mentioned, the one by R. L. Pfyffer in wax, now in Lucerne, the other by J. R. Meyer of Aarau and Müller of Engelberg in papier mâché, now in Zurich. Globes of the usual commercial type were manufactured in France by Delisle (1700), Forbin (1710–1731), R. and J. de Vaugondy (1752), Lalande (1771); in England by E. and G. Adams (1710–1766); Germany by Homann and Seutter (1750). A hollow celestial globe 18 ft. in diameter was set up by Dr Roger Long at Cambridge; the terrestrial globe which Count Ch. Gravie of Vergennes presented to Louis XVI. in 1787 had a diameter of 26 metres, or 85 ft.
Modern Cartography.—The compiler of maps of the present day enjoys many advantages not enjoyed by men similarly occupied a hundred years ago. Topographical surveys are gradually extending, and explorers of recent years are better trained for their work than they were a generation ago, whilst technical processes of recent invention—such as lithography, photography and heliogravure—facilitate or expedite the completion of his task. This task, however, has grown more difficult and exacting. Mere outline maps, such as formerly satisfied the public, suffice no longer. He is called upon more especially to give a satisfactory delineation of the ground, he must meet the requirements of various classes of the public, and be prepared to record cartographically all the facts of physical or political geography which are capable of being recorded on his maps. The ingenuity of the compiler is frequently taxed when called upon to illustrate graphically the results of statistical information of every description.
Germany since the middle of the 19th century has become the headquarters of scientific cartography. This is due as much to the inspiriting teachings of Ritter and Humboldt as to the general culture and scientific training combined with technical skill commanded by the men who more especially devote themselves to this branch of geography, which elsewhere is too frequently allowed to fall into the hands of mere mechanics. Men like H. Berghaus (1797–1884), H. Kiepert (1818–1899), and A. Petermann (1822–1878) must always occupy a foremost place in the history of cartography. Among the geographical establishments of Germany, that founded by Justus Perthes (1785), at Gotha, occupies the highest rank. Among its publications are A. Stieler’s Hand-Atlas (1817–1832), K. von Spruner’s Historical Atlas (1438–1488), H. Berghaus’ Physical Atlas (1838–1842), E. von Sydow’s Wall Maps for Schools (1838–1840) and School Atlas (1847). The titles of these atlases survive, though the authors of the original editions are long dead, and the maps have been repeatedly superseded by others bringing the information up to the date of publication. To the same firm we are indebted for Petermann’s Mitteilungen, started in 1855 by A. Petermann, after whose death in 1902 they were successively edited by E. Behm, A. Supan and P. Langhans, as also the Geographisches Jahrbuch (since 1866), at first edited by E. Behm, afterwards by Professor H. Wagner. Among other geographical institutes in Germany which deserve mention are the Weimar Institut, founded in 1791 by F. J. Bertuch, and directed in 1845–1852 by H. Kiepert; Paul Fleming at Glogau (K. Sohr’s Handatlas, 1845), A. Ravenstein at Frankfort, D. Reimer at Berlin (H. Kiepert, Handatlas, 1860); R. Andree (Hand-Atlas, 1880), and E. Debes (Hand-Atlas, 1894) in Leipzig, and E. Hölzer in Vienna (Vincenz von Haardt’s maps). France is represented by the publishing firms of Ch. Delagrave (Levaseur’s maps), Hachette (Vivien de St Martin’s Atlas universel, in progress since 1875, F. Schrader’s Atlas de géographie moderne, 1880), and Armand Colin (Vidal de la Blache’s Atlas général, 1894). In Great Britain A. Arrowsmith established himself in London in 1770 (General Atlas, 1817), but the cartographical business ceased on the death of John Arrowsmith in 1873. John Walker, to whose initiative the charts published by the admiralty are indebted for the perspicuous, firm and yet artistic execution, which facilitate their use by the mariner, was also the author of the maps published by the Society for the Diffusion of Useful Knowledge (1820–1840). Among more recent firms are W. and A. K. Johnston (founded 1825; Royal Atlas, 1855); J. Bartholomew & Co., now carried on by J. G. Bartholomew (Reduced Survey maps, Atlas of the World’s Commerce, 1906); Philip & Sons (Imperial Atlas, 1890; Systematic Atlas by E. G. Ravenstein, 1894; Mercantile Marine Atlas, 1904, globes), and E. Stanford (London Atlas).
In 1890 Professor A. Penck proposed to prepare a map of the world, including the oceans, on a scale of 1 : 1,000,000, and his scheme was promised the support of a committee which met in London in 1909, and upon which were represented the leading powers of the world. Maps on that scale of a great part of Africa, Asia and America have been published by British, French, German and United States authorities. A bathymetrical chart of the oceans, by Professor J. Thoulet was published in 1904 at the expense of Prince Albert of Monaco.
Reliefs from printed maps were first produced by Bauerkeller of Darmstadt and Dondorf at Frankfort, from originals furnished by A. Ravenstein (1838–1844). The exaggeration in altitude, on these maps and on those of a later date and on a larger scale, was very considerable. No such exaggeration exists in the case of reliefs of parts of the Alps, on a large scale, by P. Keil and Pelikan (1890), X. Imfeld (1891), P. Oberlerchner (1891–1895), C. Perron (1893–1900), F. Becker (1900), A. Heim (1904) and others. A relief globe was first suggested in a letter of M. Maestlin to J. Kepler (1596). The first globe of this description for the use of the blind, was made by A. Zeune in 1810. H. Erben is the author of a rough relief on a convex surface (1842), but the finest example of this description is a relief of Italy, by César Pomba and H. Fritsche, on a scale of 1 : 1,000,000 and without exaggeration of heights (1880–1884). A map of Italy in the baptistery of St Peter at Rome has occasionally been described as a relief, though it is merely a rude outline map of Italy, by Carlo Fontana (1698), carved into a convex surface.
Several globes of unusual dimensions were produced in the course of last century. That which Colonel Langlois erected in the Champs Elysées (1824) had a diameter of 39 metres. James Wyld’s hollow globe, or “Georama,” diam. 18 metres, occupied Leicester Square until swept away as a nuisance. The giant globe proposed by Elisée Reclus in 1895 has never been erected; he has, however, produced maps on a concave surface, as suggested by J. D. Hauber in 1742.
Authorities.—The history of maps is dealt with ably in Vivien de Saint Martin’s Histoire de la géographie (Paris, 1875), and in Peschel’s Geschichte der Erdkunde (2nd ed. by Sophus Ruge, Berlin, 1877), as also by W. Wollkenhauer (Leitfaden zur Geschichte der Kartographie, Breslau, 1895), and H. Zondervan (Allgemeine Kartenkunde, Leipzig, 1901). J. Lelewel’s Geographie du moyen âge, with an atlas (Brussels, 1850–1857), has in part been superseded by more recent researches. There are, however, a number of works, beautifully illustrated, which deal fully with particular periods of the subject. Among these may be mentioned Konrad Miller’s Die ältesten Weltkarten (Stuttgart, 1895–1897), which only deals with maps not influenced by the ideas of Ptolemy. The contents of the following collections are more varied in their nature, viz. E. F. Jomard’s Monuments de la géographie (Paris, 1862), Santarem’s Atlas composé de mappemondes et de portulans, &c. (Paris, 1842–1853, 78 plates). A. E. Nordenskiöld’s Facsimile Atlas (Stockholm, 1889), Gabriel Marcell, Choix de cartes et de mappemondes XIVe et XVe siècles (Paris, 1896). C. H. Coote’s Remarkable Maps of the XVth, XVIth and XVIIth Centuries reproduced in their Original Size (Amsterdam, 1894–1897), and Bibliotheca lindesiana (London, 1898) with facsimiles of the Harleian and other Dieppese maps of the 16th century. Nautical charts are dealt with in A. E. Nordenskiöld’s Periplus (Stockholm, 1869), and Th. Fischer’s Sammlung mittelälterlicher Welt- und Seekarten (Vienna, 1886). The discovery and mapping of America are illustrated by F. Kunstmann’s Entdeckung Amerikas (Munich, 1859), K. Kretschmer’s Atlas zur Entdeckung Amerikas (Berlin, 1892), G. Marcel’s Reproductions de cartes et de globes relatives à la découverte de l’Amérique du XVIe au XVIIIe siècle (Paris, 1893) and E. L. Stevenson’s Maps Illustrating the early Discovery and Exploration of America, 1502–1530 (New Brunswick, N.J., 1906). In addition to these collections, numerous single maps have been published in geographical periodicals or separately. See also V. Hantzsch and L. Schmidt, Kartog. Denkmäler zur Entdeckungsgeschichte von Amerika, Asien, Australien und Afrika aus der k. Bibliothek zu Dresden (Leipzig, 1903), and the Crown Collection of photographs of American maps (1600–1800), selected and edited by A. B. Hulbert (Cleveland, 1904–1909).
For reports on the progress of cartography, see Geographisches Jahrbuch (Gotha, since 1866); for announcements of new publications, Bibliotheca geographica, published annually by the Berlin Geographical Society, and to the geographical Journal (London).
Topographical Surveys.
The year 1784 marks the beginning of the ordnance survey, for in that year Major-General Roy measured a base line of 27,404 ft. on Hounslow Heath. Six additional base lines were measured up to 1849, including the Lough Foyle, in 1827–1828, and that on Salisbury Plain, in United Kingdom. 1849. The primary triangulation was only completed in 1858, but in the meantime, in 1791, the detail survey had begun. At first it was merely intended to produce a map sufficiently accurate on a scale of 1 in. to a mile (1 : 63,360). Ireland having been surveyed (1824–1842) on a scale of 6 in. to a mile (1 : 10,560), it was determined in 1840, after the whole of England and Wales, with the exception of Lancashire and Yorkshire, had been completed on one-inch scales, to adopt that scale for the whole of the United Kingdom. Finally, in 1854, a cadastral survey of the whole of the United Kingdom, only excepting uncultivated districts, was resolved upon, on a scale of 1 : 2500, still larger scales (1 : 500 or 1 : 1000) being adopted for town plans. Parish boundaries are laid down with the help of local meresmen appointed by justices at quarter sessions. The horizontal contours are based upon instrumental measurement, and as a whole these ordnance maps were undoubtedly superior in accuracy, with rare exceptions, to similar maps published by foreign governments. Even though the hill hachures on the older one-inch maps are not quite satisfactory, this deficiency is in a large measure compensated for by the presence of absolutely trustworthy contours. Originally the maps were engraved on copper, and the progress of publication was slow; but since the introduction of modern processes, such as electrotyping (in 1840), photography (in 1855) and zincography (in 1859), it has been rapid. A plan, the engraving of which formerly took two years, can now be produced in two days.
The one-inch map for the whole of the United Kingdom was completed in 1890. It covers 697 sheets (or 488 of a “new series” in large sheets), and is published in three editions, viz. (a) in outline, with contours in black, (b) with hills hachured in brown or black, and (c) printed in five colours. Carefully revised editions of these and of the other maps are brought out at intervals of 15 years at most. Since 1898 the department has also published maps on a smaller scale, viz. a map of England and Wales, on a scale of 2 m. to 1 in., in two editions, both printed in colour, the one with hills stippled in brown, the other coloured on the “layer system” as a strata-relief map; a map of the United Kingdom on a scale of 4 m. to 1 in., also in two editions, the one in outline, showing five classes of roads and parish boundaries, the other in colours, with stippled hills; a map on a scale of 10 m. to 1 in., also in two editions, and finally a map of the United Kingdom on a scale of 1 : 1,000,000.
The geological surveys of Great Britain and Ireland were connected from 1832 to 1853 with the ordnance survey, but are now carried on independently. The ordnance survey, too, no longer depends on the war office but upon the board of agriculture and fisheries. A Bathymetrical Survey of the Freshwater Lochs of Scotland, under the direction of Sir John Murray and L. Pullar, was completed in 1908, and the results published by the Royal Geographical Society.
Proposals for a new map of France, to replace the famous Cassini map of 1744–1793 were made in 1802 and again by R. Bonne in 1808, but owing to the wars then devastating Europe no steps were taken until 1817, and the Carte de France de l’état major on a scale of 1 : 80,000 was France. only completed in 1880. It is engraved on copper. The hachured hills are based upon contours, and are of admirable commensurability. It has served as a basis for a Carte de la France, published by the Service Vicinal on a scale of 1 : 100,000, in 596 sheets, and of a general map prepared by the ministère des travaux publics on a scale of 1 : 200,000 in 80 sheets. On both these maps the hills are printed in grey chalk. A third topographical map of France is being published in accordance with the recommendation of a committee presided over by General de la Noix in 1897. The surveys for this map were begun in 1905. The maps are based upon the cadastral plans (1 : 1000), thoroughly revised and connected with the triangulation of France and furnished with contours at intervals of 5 m. by precise measurement. These minutes are published on a scale of 1 : 10,000 or 1 : 20,000 for mountain districts, while the scale of the general map is 1 : 50,000. Each sheet is bounded by parallels and meridians. The hills are shown in brown contours at intervals of 10 m. and grey shading in chalk (Berthaut, La Carte de France, 1750–1898; Paris, 1899). A geological map of France on a scale of 1 : 80,000 is nearly completed, there are also a map (1 : 500,000) by Carez and Vasseur, and an official Carte géologique (1 : 1,000,000; 1906).
By the middle of the 19th century topographical maps of the various German states had been completed, and in several instances surveys of a more exact nature had been completed or begun, when in 1878 the governments of Prussia, Saxony, Bavaria and Württemberg agreed to supersede Germany. local maps by publishing a map of the empire (Reichskarte) in 674 sheets on a scale of 1 : 100,000. The earlier sheets of this excellent map were lithographed, but these are gradually being superseded by maps engraved on copper. Colour-printing is employed since 1901. The hills are hachured and in some instances contours at intervals of 50 metres are introduced. The map was completed in 1909, but is continually undergoing renewal. The Messtischblätter, called Positionsblätter in Bavaria, are on a scale of 1 : 25,000. The older among them leave much to be desired, but those of a later date are satisfactory. This applies more especially to the maps of Saxony (since 1879) and Württemberg (since 1893). The features of the ground on most of these maps are shown by contours at intervals of 10 metres. The map produced on this large scale numbers over 5000 sheets, and is used as a basis for the geological surveys carried on in several of the states of Germany. A general map of the German Empire (Uebersichtskarte) on a scale of 1 : 200,000, in 196 sheets, is in progress since 1893. It is printed in three colours, and gives contours at intervals of 10 metres. In addition to these maps there are D. G. Reymann’s well-known Specialkarte von Mittel Europa (1 : 200,000), acquired by the Prussian government in 1874 (it will ultimately consist of 796 sheets), a government and Liebenow’s map of central Europe (1 : 300,000) and C. Vogel’s beautiful map of Germany (1 : 500,000).
The Specialkarte of Austria-Hungary on a scale of 1 : 75,000 (765 sheets), based upon a triangulation and cadastral surveys (1816–1867), was completed in 1889, and published in heliogravure. This map was repeatedly revised, but as it no longer met modern requirements as to Austria-Hungary. accuracy the director of the military geographical establishment at Vienna, Field Marshal Chr. von Steeb, in 1896, organized what practically amounts to a re-survey of the entire monarchy, to be completed in 75 years. At the same time the cadastral plans, reduced to a scale of 1 : 25,000, are being published in photo-lithography. A general map of central Europe in 283 sheets published by the Austrian government (1 : 200,000) includes nearly the whole of the Balkan Peninsula.
The famous map of Switzerland, with which is associated the name of General H. Dufour (d. 1875), is based upon a triangulation (1809–1833) and surveys on a scale of 1 : 25,000 for the lowlands, 1 : 50,000 for the alpine districts, and was published (1842–1865) on a scale of 1 : 100,000. Switzerland. The hills are hachured, the light, in the case of the loftier regions, being supposed to fall obliquely. The original surveys, carefully revised, have been published since 1870 as a Topographical Atlas of Switzerland—the so-called Siegfried Atlas, in 552 sheets. They are printed in three colours, contours at intervals of 10 and 20 metres being in brown, incidental features (ravines, cliffs, glaciers) in black or blue. To mountain-climbers these contour maps are invaluable, but for ordinary purposes “strata maps,” such as J. M. Ziegler’s hypsometric maps (1856) or so-called “relief maps,” which attempt to delineate the ground so as to give the impression of a relief, are generally preferred.
The new survey of Belgium was completed in 1872 and there have been published 527 plane-table sections or planchettes on a scale of 1 : 20,000 (1866–1880), a “Carte topographique de la Belgique,” in 72 sheets, on a scale of 1 : 40,000 (1861–1883), and a more recent map in 26 sheets Belgium. on a scale of 1 : 100,000 (1903–1912). The last is printed in five colours, the ground is shown in contours of 10 metres interval and grey stippling.
The new survey of the Netherlands, based upon General Krayenhoff’s primary triangulation (1802–1811) was completed in 1855. The results have been published on a scale of 1 : 25,000 (776 sheets, since 1866), 1 : 50,000 (Topographic and Military Map, 62 sheets, 1850–1864, and a Holland. Waterstaatskaart, 1864–1892), and 1 : 200,000 (Topographical Atlas, 21 sheets, 1868–1871).
In Denmark, on the proposal of the Academy of Science, a survey was carried out in 1766–1825, but the maps issued by the Danish general staff depend upon more recent surveys. These include plane-table sections (Maalebordsblade), 1209 sheets on a scale of 1 : 20,000, with contours Denmark. at intervals of 5 to 10 ft., published since 1830; Atlasblade of Jutland and of De Danske Öer, on a scale of 1:40,000, the former in 131 sheets, since 1870, the latter, on the same scale, in 94 sheets, since 1890, and still in progress, and a general staff map on a scale of 1:100,000, in 68 sheets, since 1890. Maps of the Faroer and of Iceland have likewise been issued.
Modern surveys in Sweden date from the organization of a corps of “Landemätare,” known since 1874 as a topographical department of the general staff. The maps issued by this authority include one of southern Sweden, 1:100,000, another of northern Sweden, 1:200,000, and a general Scandinavia. map on a scale of 1:1,000,000. In Norway a geographical survey (Opmaaling) has been in progress since 1783, but the topographical map of the kingdom on a scale of 1:100,000 in 340 sheets, has not yet been completed.
Of Russia in Europe only the more densely peopled governments have been surveyed, since 1816, in the manner of other European countries, while for most regions there are only so-called “military surveys.” The most readily available map of the whole country is the 10-verst Russia. map (1:420,000), known as General J. A. Strelbitzki’s, and published 1865–1880. A topographic map (1:126,000) embracing the whole of western Russia, with Poland and the country of the Don Cossacks, is designed to be extended over the whole empire. Certain governments—Moscow, Kief, Volhynia, Bessarabia, the Crimea, &c.—have been published on a scale of 1:24,000, while Finland, as far as 61° N., was re-surveyed in 1870–1895, and a map on a scale of 1:42,000 is approaching completion.
Surveys in Asiatic Russia are conducted by the topographical departments organized at Orenburg, Tashkent, Omsk, Irkutsk and Tiflis. To the latter we are indebted for a valuable map of Caucasia, 1:210,000, which since the first publication (1863–1885) has undergone careful revision. The Siberian departments have published a number of maps on a scale of 1:420,000. In addition to these the survey for the Trans-Siberian railway has been published on a scale of 1:630,000, as also maps of the Russo-Chinese frontier districts, 1:210,000 and 1:1,168,000. A map of Asiatic Russia, 1:420,000, by Bolshef, in 192 sheets, is in course of publication.
Passing to southern Europe we find that Portugal has completed
a Charta chorographica (1:100,000) since 1856. In
Spain a plane-table survey on a scale of 1:20,000
has been in progress since 1870, but of the map of
Spain in 1078 sheets on a scale of 1:50,000 only
Portugal
and Spain.
150 had been issued by the depósito de la guerra up to 1910.
Meanwhile reference may be made to B. F. Coello’s Atlas de la
España (1848–1890), the maps of which are on a scale of
1:200,000.
In Italy Tavulette rilevata on a scale of 1:25,000 or 1:50,000, with contours, based on surveys made 1862–1890, are being published, and a Carta del regno d’Italia, 1:100,000, is practically complete. There are a Carta idrologica and a Carta geologica on the same scale, Italy.and a Carta orografica on a scale of 1:500,000.
Greece is still dependent upon foreigners for its maps, among which the Carte de Grèce (1:200,000) from rapid surveys made by General Palet in 1828, was published in a new edition in 1880. A similar map, mainly based upon surveys made by Austrian officers and revised by H. Kiepert Greece. (1:300,000), was published by the Military Geographical Institute of Vienna in 1885. Far superior to these maps is the Karte von Attika (1:100,000 and 1:25,000) based upon careful surveys made by Prussian officers and published by E. Curtius and J. H. Kaupert on behalf of the German Archaeological Institute in Athens (1878), or A. Philippson’s map of the Peloponnese (1:300,000; 1901).
For maps of the Balkan Peninsula we are still largely indebted to the rapid surveys carried on by Austrian and Russian officers. The Austrian map of central Europe embraces the whole of the Balkan Peninsula on a scale of 1:200,000; the Russian surveys (1877–1879) are Balkan States. embodied in a map of the eastern part of the Balkan on a scale 1:126,000, and a map of Bulgaria and southern Rumelia, on a scale 1:200,000, both published in 1883. A map of Turkey in Europe, scale 1:210,000, was published by the Turkish general staff (1899), and another map, scale 1:250,000, by the intelligence division of the British war office is in progress since 1906. Bosnia and Herzegovina are now included with the surveys of the Austrian Empire, the kingdom of Servia has been surveyed (1880–1891) and the results published on a scale of 1:75,000; in eastern Rumania surveys have been in progress since 1874 and the results have been published on a scale of 1:50,000; a general map of the entire kingdom, scale 1:200,000, was published in 1906–1907; a map of Montenegro (1:75,000), based on surveys by Austrian and Russian officers, was published at Vienna in 1894.
In Asiatic Turkey several districts of historical interest have been surveyed, and surveys have likewise been made in the interest of railways, or by boundary commissions, but there is no such thing as a general survey carried on under the direction of government. We are thus, Asia. to a large extent, still dependent upon compilations, such as R. Kiepert’s Asia Minor (1:400,000; 1904–1908), a map of eastern Turkey in Asia, Syria and western Persia (1:2,000,000; 1910), published by the Royal Geographical Society, or a Russian general map (1:630,000, published 1880–1885). Among maps based upon actual surveys those of Palestine, by Lieutenant G. R. Conder and H. H. (afterwards Lord) Kitchener (1:63,360, 1880), of the Sinai Peninsula by Sir C. W. Wilson and H. S. Palmer (1:126,730, 1870), of Arabia Petraea by Dr A. Musil (1:300,000, 1907) or of the Aden territory (1905) are among the more interesting. Of Cyprus an excellent map from surveys by Major (Lord) H. H. Kitchener was published in 1884 (1:63,360).
In the case of Persia and Afghanistan we are still dependent upon compilations such as a Russian staff map (1:840,000, published in 1886), Colonel Sir T. H. Holdich’s map of Persia (1:1,014,000, Simla, 1897–1899), or a smaller map (1:2,028,000 and 1:4,056,000), published by the geographical division of the general staff. The settlement of boundaries in northern Afghanistan (1883) and in Seistan (1870) has necessitated surveys of some interest.
A trigonometrical survey of British India was begun in 1800 and the country can now boast of a survey which in most respects is equal to those of most European states. The surveys are made on scales varying according to the necessities of the case or the nature of the country, and they have been extended since 1862 beyond the boundaries of India proper. Revenue surveys for land settlement are published on a scale of 1:4000, but the usual scale for topographical maps is 1:63,360. An Indian Atlas, on a scale of 1:255,660, includes also Ceylon and the Malay Peninsula, but although begun so long ago as 1827 many of its sheets are unpublished. There are in addition an official map of India (1:1,000,000), the first edition of which was published in 1903, as also maps of the great provinces of India, including Burma, all on a scale of 1:2,827,520, and a variety of physical and statistical maps. Ceylon and the Straits Settlements, with the Federal Malay States, have their own surveyors-general. The British North Borneo Company published a Map of British North Borneo, on a scale of 1:633,600 (1905).
In Siam a regular survey was organized by Mr J. McCarthy (1881–1883), a former official of the Indian survey, which did good work in connexion with the determination of the Franco-Siamese frontier (1906). The surveys are made on the scales of 1:4000, 1:31,680 and 1:63,360.
In French Indo-China surveys have been in progress since 1881. The Bureau of the Indo-Chinese general staff, has published a map of Indo-China, including Cambodia, in 45 sheets (1:200,000, 1895), while to the service géographique de l’Indo-Chine, organized in 1899, we owe a Carte de l’Indo-Chine (1:500,000).
For China we are still largely dependent upon careful compilations like Baron F. von Richthofen’s Atlas von China (1:750,000, Berlin, 1885–1890) or Bretschneider’s Map of China (1:4,600,000) a new edition of which appeared at St Petersburg in 1900. There are good survey maps of the British colony of Hong-Kong, of Wei-hai-Wei and of the country around Kiao-chou, and the establishment of topographical offices at Peking and Ngan-king holds out some promise of native surveys. In the meantime large scale maps prepared by European authorities are to be welcomed, such as maps of Chih-li and Shan-tung (1:200,000), from surveys by Prussian officers, 1901–1905, maps on East China (1:1,000,000) and of Yun-nan by British, German and Indian officers, of the Indo-Chinese frontier (1:200,000, Paris 1908), and of the upper Yangtsze-kiang by S. Chevalier (Shanghai, 1900).
Japan has a regular survey department originated by Europeans and successfully carried on by natives. The primary triangulation was completed in 1880, a topographical map coloured geologically (1:200,000) was published 1889–1897, and in addition to this there are being published an agronomical map on a scale of 1:100,000 (since 1887) and others. The Japanese government has likewise published a map of Korea (1:1,000,000; 1898).
The Philippine Islands are represented in a carefully compiled map by C. W. Hodgson (1:1,115,000, New York, 1908). Of Java we possess an excellent topographical map based upon surveys made 1850–1887 (1:100,000). A similar map has been in progress for Sumatra since 1883, while the maps for the remaining Dutch Indies are still based, almost exclusively, upon flying surveys. For general purposes the Atlas der Nederlandsche Bezittingen in Oost-Indie by J. N. Stemfoort and J. J. Ten Siethoff, of which a new edition has been published since 1900, may be consulted with confidence.
In Africa nearly all the international boundaries have been carefully surveyed and marked on the ground, since 1880, and yield a good basis as a guide for the map compiler. A general map of Africa, by Colonel Lannoy de Bissy, on a scale of 1:2,000,000 was first published in 1882–1888, Africa. but is carefully revised from time to time. The geographical section of the British general staff is publishing maps of all Africa on scales of 1:250,000 and 1:1,000,000. In Egypt excellent work has been done by a survey department organized and directed by Captain H. G. Lyons up to 1909. It has published a topographical map of the Nile valley (1:50,000), an irrigation map (1:100,000), a general map (1:250,000), numerous cadastral plans, &c. Work on similar lines is carried on in the Anglo-Egyptian Sudan. Algeria has been in course of survey since 1868, Tunis since 1878, and the results have been published on scales of 1:50,000 and 1:250,000. Of Morocco there are many maps, among which several compiled by the French service géographique de l’armée, including a Carte du Maroc (1:200,000), in progress since 1909. In the British colonies of tropical and of South Africa[26] surveys for the most part are carried on actively. Of the Gambia Colony there is a map by Major E. L. Cowie (1:250,000, 1904–1905); the survey of the Gold Coast Colony is being published by Major F. G. Guggisberg since 1907 (1:125,000 and 1:200,000); southern and northern Nigeria are adequately represented on the maps of the general staff (1:250,000). The states of British South Africa have each their surveyor-general, and a reconnaissance survey has been in progress since 1903. It is based upon a careful triangulation, superintended by Sir D. Gill, and carried in 1907 within 70 m. of Lake Tanganyika. This survey is rapidly superseding other maps, such as the surveyor-general’s map of Cape Colony (1:127,000); A. Duncan’s map of the Orange River State (1:148,705; 1902–1904) and Jeppe’s map of the Transvaal (1:476,000; 1899). The results of a survey of southern Rhodesia are given on the map of the British general staff (1:500,000; 1909), while of north-eastern Rhodesia we have an excellent map compiled by C. L. Beringer in 1907 (1:1,000,000). Surveys in British Central Africa were taken up in 1894; a survey of Lake Nyasa, by Lieut. E. L. Rhoades and W. B. Phillips, was published in 1902. As regards British East Africa and Uganda, the surveys in the latter (on scales of 1:10,000 and 1:125,000) have made considerable progress. The Victoria Nyanza was surveyed by Captain B. Whitehouse (1898–1900), and the results have been published on a scale of 1:292,000. These British possessions, together with the whole of Somaliland and southern Abyssinia, are satisfactorily represented on the maps of the British general staff.
Maps of the French Africa Colonies have been published by the service géographique de l’Afrique occidental and the service géographique des colonies. A map of Senegal (1:100,000) is in progress since 1905. The official maps of the other colonies have been compiled by A. Meunier between 1902 and 1909. They include French West Africa, (1:2,000,000; 2nd ed., 1908), French Guinea (1:500,000; 1902) and the Ivory Coast and Dahomey (1:1,500,000; 1907–1908). A map of the French Congo by J. Hansen (1:1,500,000), was published in 1907. In Madagascar a topographical bureau was established by General J. S. Gallieni in 1896, and the surveys are being published since 1900 on a scale of 1:100,000.
As regards the German colonies we are dependent upon compilations by R. Kiepert, P. Sprigade and M. Moisel. Good maps of the Portuguese colonies are to be found in an Atlas colonial Portugues, a second edition of which was published by the Commissão de Cartographia in 1909. Of the Congo State we have an official map on a scale of 1:1,000,000, published in 1907. Of Italian Eritrea we have excellent maps on various scales of 1:100,000, 1:200,000 and 1:500,000, based upon surveys made between 1888 and 1900.
In the states of Australia cadastral surveys conducted by surveyors-general have been in progress for many years, as also trigonometrical surveys (Western Australia excepted), and the publication of parish and township or county maps keeps pace with the settlement of the country; but with Australia. the exception of Victoria none of these states is in possession of a topographical map equal in accuracy to similar maps published in Europe. In Victoria the so-called geodetic survey was begun in 1858; the maps are published on a scale of 1:126,730. There exists also a general map, on a scale of 1:506,930. Maps on the same scale are available of New South Wales, South Australia and Tasmania, on a scale of 1:560,000 for Western Australia, on a scale of 1:253,460 for Queensland. There are likewise maps on smaller scales, which undergo frequent revision. The map of British New Guinea is on a scale of 1:330,200 (1898). New Zealand has a good general map on a scale of 1:633,700. A trigonometrical survey was given up and only details of immediate practical use are required. The “Lands Department” of the Fiji Islands has published a map on a scale of 1:380,000 (1908).
The cadastral surveys in Canada are carried on by a commission of Crown-lands in the old provinces and by a Dominion land office, which lays out townships as in the United States, but with greater accuracy. A surveyor-general is attached to the department of the interior, North America. at Ottawa. He publishes the topographical maps (1:63,366) since 1906. They are based upon theodolite traverses 15 m. apart, and connected with the United States lake and coast surveys, the details being filled in by plane-table surveys on a scale of 1:31,680. The contours, 25 ft. apart, depend upon spirit-levelling. In the Rocky Mountains surveys photographic apparatus is successfully employed. The surveyor-general issues also “sectional maps” (1:190,000 and 1:40,000) and so-called “Standard” topographical maps for the thinly peopled west, on scales of 1:250,000 and 1:500,000. He is responsible likewise for maps of Yukon and of Labrador, supplied by the geological survey, the former on a scale of 1:380,200, the latter of 1:1,584,000. The intelligence branch of the Canadian department of military defence is publishing since 1904 topographical maps on scales of 1:63,366 and 1:126,730, with contours. A geodetic survey department, under Dr. W. F. King, chief astronomer of the Dominion, was established in 1909.
Maps of Newfoundland, orographical as well as geological, scale 1: 1,584,200, have been published.
In the United States a “geological survey” was organized in 1879, under Clarence King as director, whose successor, Major J. W. Powell, rightly conceived that it was necessary to produce good topographical maps before a geological survey could be pursued with advantage. It is under his wise guidance that the survey has attained its present efficiency. It is based upon a triangulation by the U.S. Coast and Geodetic Survey. The maps of the more densely peopled parts of the Union are published on a scale of 1 : 62,500, and those of the remainder of the country on half or a quarter of that scale. The hills are shown by contours at intervals of 10 or 100 ft. The details given are considered sufficient to admit of the selection of general routes for railways or other public works. The survey progresses at the rate of about 40,000 sq. m. annually, and in course of time it will supersede the map of the separate states, based on older surveys. A “reconnaissance” map of Alaska (on a scale of 1 : 250,000) was published in 1908.
In Mexico the surveys are in charge of a comision geografica-exploradora attached to the secretaria de Fomento, but only about 140 sheets of a Carta general on a scale of 1 : 100,000 have been published. There are also a map of the state of S. Luis Potosi (1 : 250,000), of Central America. the environs of Puebla (1 : 50,000) and a Carta general de la republica mexicana (1 : 250,000).
A useful map of Central America has been published by the topographical section of the British general staff on a scale of 1 : 170,300. Of great value for cartographical work is a careful survey, carried out by American engineers (1897–1898), for a continental railway running along the west coast from Mexico to Chile. In South America, in proportion to the area of the country, only few surveys of a thoroughly scientific nature have been made, and it is therefore satisfactory that the service géographique of the French army should be publishing, since 1900, a map of the entire continent on a scale of 1 : 1,000,000.
Colombia is but inadequately represented by rough maps. For Colombia we have F. L. Vergara y Velasco’s Atlas de geografia colombiana (1906–1908); Ecuador is fairly well represented by Th. Wolf (1892) and Hans Meier (1907); in the case of Peru we still largely depend upon Paz Soldan’s Atlas geografica (1865–1867) and A. Raimondi’s Mapa del Peru (1 : 500,000) based upon surveys made before 1869. Sir Martin Conway’s “Map of the Andes of La Paz” (1 : 600,000; 1900) as well as Major P. H. Fawcett’s survey of the Brazilian boundary (1906–1907) are welcome additions to our knowledge of Bolivia. In Chile a comision topografica was appointed as long ago as 1848, but the map produced under its auspices by Professor F. Pissis (1 : 250,000, 1870–1877), leaves much to be desired. Since that time, however, valuable maps have been published by an Oficina de mensura de tierras, by a seccion de geografia y minas connected with the department of public works, by the Oficina hidrografica, and more especially in connexion with surveys necessitated by the boundary disputes with Argentina, which were settled by arbitration in 1899 and 1902. The surveys which led to the latter were conducted by Sir Thomas Holdich.
In Venezuela a commission for producing a plano militar or military map of the country was appointed by General Castro in 1904, but little progress seems to have been made, and meantime we are dependent upon a revised edition of A. Codazzi’s map of 1840 which was published in 1884. In Brazil little or nothing is done by the central government, but the progressive states of São Paulo and Mines Gerães have commissãos geographicos e geologicos engaged in the production of topographical maps. Valuable materials have likewise been acquired by several river surveys including those of the Amazonas by Azevedo and Pinto (1862–1864) and W. Chandless (1862–1869) and of the Rio Madeira by Colonel G. Earl Church and Keller-Leuzinger (1860–1875). The proposal of a committee presided over by the Marshal H. de Beaurepaire-Rohan (1876) to prepare a map of Brazil on a scale of 1 : 200,000 has never been acted upon, and in the meantime we are dependent upon works like the Atlas do imperio do Brazil by Mendes de Almeida (1868) or the maps in our general atlases.
In Argentina an official geographical institute was established in 1879, but neither A. Seelstrang’s Atlas (1886–1892) nor H. Hoskold’s Mapa topografica (1 : 2,000,000; London, 1895), which were published by it, nor any of the numerous provincial maps are based upon scientific surveys.
It need hardly be said that hydrographic surveys have been of great service to compilers of maps. There are few coast-lines, frequented by shipping, which have not yet been surveyed in a definite manner. In this work the British hydrographic office may justly claim the credit of having contributed the chief share. Great Britain has likewise taken the lead in those deep-sea explorations which reveal to us the configuration of the sea-bottom, and enable us to construct charts of the ocean bed corresponding to the contoured maps of dry land yielded by topographical surveys. (E. G. R.)
In the construction of maps, one has to consider how a portion of spherical surface, or a configuration traced on a sphere, can be represented on a plane. If the area to be represented bear a very small ratio to the whole surface of the sphere, the matter is easy: thus, for instance, there is no difficulty in making a map of a parish, for in such cases the curvature of the surface does not make itself evident. If the district is larger and reaches the size of a county, as Yorkshire for instance, then the curvature begins to be sensible, and one requires to consider how it is to be dealt with. The sphere cannot be opened out into a plane like the cone or cylinder; consequently in a plane representation of configurations on a sphere it is impossible to retain the desired proportions of lines or areas or equality of angles. But though one cannot fulfil all the requirements of the case, we may fulfil some by sacrificing others; we may, for instance, have in the representation exact similarity to all very small portions of the original, but at the expense of the areas, which will be quite misrepresented. Or we may retain equality of areas if we give up the idea of similarity. It is therefore usual, excepting in special cases, to steer a middle course, and, by making compromises, endeavour to obtain a representation which shall not involve large errors of scale.
A globe gives a perfect representation of the surface of the earth; but, practically, the necessary limits to its size make it impossible to represent in this manner the details of countries. A globe of the ordinary dimensions serves scarcely any other purpose than to convey a clear conception of the earth’s surface as a whole, exhibiting the figure, extent, position and general features of the continents and islands, with the intervening oceans and seas; and for this purpose it is indeed absolutely essential and cannot be replaced by any kind of map.
The construction of a map virtually resolves itself into the drawing of two sets of lines, one set to represent meridians, the other to represent parallels. These being drawn, the filling in of the outlines of countries presents no difficulty. The first and most natural idea that occurs to one as to the manner of drawing the circles of latitude and longitude is to draw them according to the laws of perspective. Perhaps the next idea which would occur would be to derive the meridians and parallels in some other simple geometrical way.
 |
| Fig. 1. |
Cylindrical Equal Area Projection.—Let us suppose a model of the earth to be enveloped by a cylinder in such a way that the cylinder touches the equator, and let the plane of each parallel such as PR be prolonged to intersect the cylinder in the circle pr. Now unroll the cylinder and the projection will appear as in fig. 2. The whole world is now represented as a rectangle, each parallel is a straight line, and its total length is the same as that of the equator, the distance of each parallel from the equator is sinl(wherelis the latitude and the radius of the model earth is taken as unity). The meridians are parallel straight lines spaced at equal distances.
 |
| Fig. 2. |
This projection possesses an important property. From the
elementary geometry of sphere and cylinder it is clear that each
strip of the projection is equal in area to the zone on the model
which it represents, and that each portion of a strip is equal in
area to the corresponding portion of a zone. Thus, each
small four-sided figure (on the model) bounded by meridians
and parallels ![]() is represented on the projection by a
rectangle
is represented on the projection by a
rectangle ![]() which is of exactly the same area, and this
applies to any such figure however small. It therefore follows
that any figure, of any shape on the model, is correctly
represented as regards area by its corresponding figure on
the projection. Projections having this property are said to
be equal-area projections or equivalent projections; the
name of the projection just described is “the cylindrical
equal-area projection.” This projection will serve to exemplify
the remark made in the first paragraph that it is
possible to select certain qualities of the model which shall
be represented truthfully, but only at the expense of other
qualities. For instance, it is clear that in this case all meridian
lengths are too small and all lengths along the parallels, except
the equator, are too large. Thus although the areas are preserved
the shapes are, especially away from the equator, much
distorted.
which is of exactly the same area, and this
applies to any such figure however small. It therefore follows
that any figure, of any shape on the model, is correctly
represented as regards area by its corresponding figure on
the projection. Projections having this property are said to
be equal-area projections or equivalent projections; the
name of the projection just described is “the cylindrical
equal-area projection.” This projection will serve to exemplify
the remark made in the first paragraph that it is
possible to select certain qualities of the model which shall
be represented truthfully, but only at the expense of other
qualities. For instance, it is clear that in this case all meridian
lengths are too small and all lengths along the parallels, except
the equator, are too large. Thus although the areas are preserved
the shapes are, especially away from the equator, much
distorted.
The property of preserving areas is, however, a valuable one when the purpose of the map is to exhibit areas. If, for example, it is desired to give an idea of the area and distribution of the various states comprising the British Empire, this is a fairly good projection. Mercator’s, which is commonly used in atlases, preserves local shape at the expense of area, and is valueless for the purpose of showing areas.
Many other projections can be and have been devised, which depend for their construction on a purely geometrical relationship between the imaginary model and the plane. Thus projections may be drawn which are derived from cones which touch or cut the sphere, the parallels being formed by the intersection with the cones of planes parallel to the equator, or by lines drawn radially from the centre. It is convenient to describe all projections which are derived from the model by a simple and direct geometrical construction as “geometrical projections.” All other projections may be known as “non-geometrical projections.” Geometrical projections, which include perspective projections, are generally speaking of small practical value. They have loomed much more largely on the map-maker’s horizon than their importance warrants. It is not going too far to say that the expression “map projection” conveys to most well-informed persons the notion of a geometrical projection; and yet by far the greater number of useful projections are non-geometrical. The notion referred to is no doubt due to the very term “projection,” which unfortunately appears to indicate an arrangement of the terrestrial parallels and meridians which can be arrived at by direct geometrical construction. Especially has harm been caused by this idea when dealing with the group of conical projections. The most useful conical projections have nothing to do with the secant cones, but are simply projections in which the meridians are straight lines which converge to a point which is the centre of the circular parallels. The number of really useful geometrical projections may be said to be four: the equal-area cylindrical just described, and the following perspective projections—the central, the stereographic and Clarke’s external.
Perspective Projections.
In perspective drawings of the sphere, the plane on which the representation is actually made may generally be any plane perpendicular to the line joining the centre of the sphere and the point of vision. If V be the point of vision, P any point on the spherical surface, then p, the point in which the straight line VP intersects the plane of the representation, is the projection of P.
 |
| Fig. 3. |
Orthographic Projection.—In this projection the point of vision is at an infinite distance and the rays consequently parallel; in this case the plane of the drawing may be supposed to pass through the centre of the sphere. Let the circle (fig. 3) represent the plane of the equator on which we propose to make an orthographic representation of meridians and parallels. The centre of this circle is clearly the projection of the pole, and the parallels are projected into circles having the pole for a common centre. The diameters aa′, bb′ being at right angles, let the semicircle bab′ be divided into the required number of equal parts; the diameters drawn through these points are the projections of meridians. The distances of c, of d and of e from the diameter aa′ are the radii of the successive circles representing the parallels. It is clear that, when the points of division are very close, the parallels will be very much crowded towards the outside of the map; so much so, that this projection is not much used.
For an orthographic projection of the globe on a meridian plane let qnrs (fig. 4) be the meridian, ns the axis of rotation, then qr is the projection of the equator. The parallels will be represented by straight lines passing through the points of equal division; these lines are, like the equator, perpendicular to ns. The meridians will in this case be ellipses described on ns as a common major axis, the distances of c, of d and of e from ns being the minor semiaxes.
 |  | |
| Fig. 4. | Fig. 5. |
Let us next construct an orthographic projection of the sphere on the horizon of any place.
 |
| Fig. 6.—Orthographic Projection. |
Set off the angle aop (fig. 5) from the radius oa, equal to the latitude. Drop the perpendicular pP on oa, then P is the projection of the pole. On ao produced take ob = pP, then ob is the minor semiaxis of the ellipse representing the equator, its major axis being qr at right angles to ao. The points in which the meridians meet this elliptic equator are determined by lines drawn parallel to aob through the points of equal subdivision cdefgh. Take two points, as d and g, which are 90° apart, and let ik be their projections on the equator; then i is the pole of the meridian which passes through k. This meridian is of course an ellipse, and is described with reference to i exactly as the equator was described with reference to P. Produce io to l, and make lo equal to half the shortest chord that can be drawn through i; then lo is the semiaxis of the elliptic meridian, and the major axis is the diameter perpendicular to iol.
For the parallels: let it be required to describe the parallel whose co-latitude is u; take pm = pn = u, and let m′n′ be the projections of m and n on oPa; then m′n′ is the minor axis of the ellipse representing the parallel. Its centre is of course midway between m′ and n′, and the greater axis is equal to mn. Thus the construction is obvious. When pm is less than pa the whole of the ellipse is to be drawn. When pm is greater than pa the ellipse touches the circle in two points; these points divide the ellipse into two parts, one of which, being on the other side of the meridian plane aqr, is invisible. Fig. 6 shows the complete orthographic projection.
 |
| Fig. 7. |
 |
| Fig. 8. |
Stereographic Projection.—In this case the point of vision is on the surface, and the projection is made on the plane of the great circle whose pole is V. Let kpl V (fig. 7) be a great circle through the point of vision, and ors the trace of the plane of projection. Let c be the centre of a small circle whose radius is cp = cl; the straight line pl represents this small circle in orthographic projection.
We have first to show that the stereographic projection of the small circle pl is itself a circle; that is to say, a straight line through V, moving along the circumference of pl, traces a circle on the plane of projection ors. This line generates an oblique cone standing on a circular base, its axis being cV (since the angle pVc = angle cVl); this cone is divided symmetrically by the plane of the great circle kpl, and also by the plane which passes through the axis Vc, perpendicular to the plane kpl. Now Vr·Vp, being = Vo sec kVp·Vk cos kVp = Vo·Vk, is equal to Vs·Vl; therefore the triangles Vrs, Vlp are similar, and it follows that the section of the cone by the plane rs is similar to the section by the plane pl. But the latter is a circle, hence also the projection is a circle; and since the representation of every infinitely small circle on the surface is itself a circle, it follows that in this projection the representation of small parts is strictly similar. Another inference is that the angle in which two lines on the sphere intersect is represented by the same angle in the projection. This may otherwise be proved by means of fig. 8, where Vok is the diameter of the sphere passing through the point of vision, fgh the plane of projection, kt a great circle, passing of course through V, and ouv the line of intersection of these two planes. A tangent plane to the surface at t cuts the plane of projection in the line rvs perpendicular to ov; tv is a tangent to the circle kt at t, tr and ts are any two tangents to the surface at t. Now the angle vtu (u being the projection of t) is 90° − otV = 90° − oVt = ouV = tuv, therefore tv is equal to uv; and since tvs and uvs are right angles, it follows that the angles vts and vus are equal. Hence the angle rts also is equal to its projection rus; that is, any angle formed by two intersecting lines on the surface is truly represented in the stereographic projection.
In this projection, therefore, angles are correctly represented and every small triangle is represented by a similar triangle. Projections having this property of similar representation of small parts are called orthomorphic, conform or conformable. The word orthomorphic, which was introduced by Germain[27] and adopted by Craig,[28] is perhaps the best to use.
Since in orthomorphic projections very small figures are correctly represented, it follows that the scale is the same in all directions round a point in its immediate neighbourhood, and orthomorphic projections may be defined as possessing this property. There are many other orthomorphic projections, of which the best known is Mercator’s. These are described below.
We have seen that the stereographic projection of any circle of the sphere is itself a circle. But in the case in which the circle to be projected passes through V, the projection becomes, for a great circle, a line through the centre of the sphere; otherwise, a line anywhere. It follows that meridians and parallels are represented in a projection on the horizon of any place by two systems of orthogonally cutting circles, one system passing through two fixed points, namely, the poles; and the projected meridians as they pass through the poles show the proper differences of longitude.
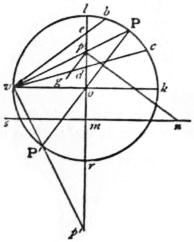 |
| Fig. 9. |
 |
| Fig. 10. |
To construct a stereographic projection of the sphere on the horizon of a given place. Draw the circle vlkr (fig. 9) with the diameters kv, lr at right angles; the latter is to represent the central meridian. Take koP equal to the co-latitude of the given place, say u; draw the diameter PoP′, and vP, vP′ cutting lr in pp′: these are the projections of the poles, through which all the circles representing meridians have to pass. All their centres then will be in a line smn which crosses pp′ at right angles through its middle point m. Now to describe the meridian whose west longitude is ω, draw pn making the angle opn = 90° − ω, then n is the centre of the required circle, whose direction as it passes through p will make an angle opg = ω with pp′. The lengths of the several lines are
Again, for the parallels, take Pb = Pc equal to the co-latitude, say c, of the parallel to be projected; join vb, vc cutting lr in e, d. Then ed is the diameter of the circle which is the required projection; its centre is of course the middle point of ed, and the lengths of the lines are
The line sn itself is the projection of a parallel, namely, that of which the co-latitude c = 180° − u, a parallel which passes through the point of vision.
Notwithstanding the facility of construction, the stereographic projection is not much used in map-making. It is sometimes used for maps of the hemispheres in atlases, and for star charts.
External Perspective Projection.—We now come to the general case in which the point of vision has any position outside the sphere. Let abcd (fig. 10) be the great circle section of the sphere by a plane passing through c, the central point of the portion of surface to be represented, and V the point of vision. Let pj perpendicular to Vc be the plane of representation, join mV cutting pj in f, then f is the projection of any point m in the circle abc, and ef is the representation of cm.
Let the angle com = u, Ve = k, Vo = h, ef = ρ; then, since ef: eV = mg : gV, we have ρ = k sin u/(h + cos u), which gives the law connecting a spherical distance u with its rectilinear representation ρ. The relative scale at any point in this system of projection is given by
| σ = dρ / du, σ′ = ρ / sin u, |
| σ = k (1 + h cos u) / (h + cos u)2; σ′ = k / (h + cos u), |
the former applying to measurements made in a direction which passes through the centre of the map, the latter to the transverse direction. The product σσ′ gives the exaggeration of areas. With respect to the alteration of angles we have Σ = (h + cos u) / (l + k cos u), and the greatest alteration of angle is
| sin−1 ( | h − 1 | tan2 | u | ). |
| h + 1 | 2 |
This vanishes when h = 1, that is if the projection be stereographic; or for u = 0, that is at the centre of the map. At a distance of 90° from the centre, the greatest alteration is 90° − 2 cot−1 √h. (See Phil. Mag. 1862.)
Clarke’s Projection.—The constants h and k can be determined, so that the total misrepresentation, viz.:
shall be a minimum, β being the greatest value of u, or the spherical radius of the map. On substituting the expressions for σ and σ′ the integration is effected without difficulty. Put
| λ = (1 − cos β) / (h + cos β); ν = (h − 1) λ, |
| H = ν − (h + 1) loge (λ + 1), H′ = λ (2 − ν + 13ν2) / (h + 1). |
Then the value of M is
When this is a minimum,
∴ kH′ + H = 0; 2 dH / dh + kdhH′ / dh = 0.
Therefore M = 4 sin2 12β − H2/H1, and h must be determined so as to make H2 : H′ a maximum. In any particular case this maximum can only be ascertained by trial, that is to say, log H2 − log H′ must be calculated for certain equidistant values of h, and then the particular value of h which corresponds to the required maximum can be obtained by interpolation. Thus we find that if it be required to make the best possible perspective representation of a hemisphere, the values of h and k are h = 1.47 and k = 2.034; so that in this case
| ρ = | 2.034 sin u | . |
| 1.47 + cos u |
For a map of Africa or South America, the limiting radius β we may take as 40°; then in this case
| ρ = | 2.543 sin u | . |
| 1.625 + cos u |
For Asia, β = 54, and the distance h of the point of sight in this case is 1.61. Fig. 11 is a map of Asia having the meridians and parallels laid down on this system.
 |
| Fig. 11. |
Fig. 12 is a perspective representation of more than a hemisphere, the radius β being 108°, and the distance h of the point of vision, 1.40.
 |
| Fig. 12.—Twilight Projection. Clarke’s Perspective Projection for a Spherical Radius of 108°. |
The co-ordinates xy of any point in this perspective may be expressed in terms of latitude and longitude of the corresponding point on the sphere in the following manner. The co-ordinates originating at the centre take the central meridian for the axis of y and a line perpendicular to it for the axis of x. Let the latitude of the point G, which is to occupy the centre of the map, be γ; if φ, ω be the latitude and longitude of any point P (the longitude being reckoned from the meridian of G), u the distance PG, and μ the azimuth of P at G, then the spherical triangle whose sides are 90° − γ, 90° − φ, and u gives these relations—
| sin u sin μ = cos φ sin ω, |
| sin u cos μ = cos γ sin φ − sin γ cos φ cos ω, |
| cos u = sin γ sin φ + cos γ cos φ cos ω. |
Now x = ρ sin μ, y = ρ cos μ, that is,
| x | = | cos φ sin ω | , |
| k | h + sin γ sin φ + cos γ cos φ cos ω |
| y | = | cos γ sin φ − sin γ cos φ cos ω | , |
| k | h + sin γ sin φ + cos γ cos φ cos ω |
by which x and y can be computed for any point of the sphere. If from these equations we eliminate ω, we get the equation to the parallel whose latitude is φ; it is an ellipse whose centre is in the central meridian, and its greater axis perpendicular to the same. The radius of curvature of this ellipse at its intersection with the centre meridian is k cos φ / (h sin γ + sin φ).
The elimination of φ between x and y gives the equation of the meridian whose longitude is ω, which also is an ellipse whose centre and axes may be determined.
The following table contains the computed co-ordinates for a map of Africa, which is included between latitudes 40° north and 40° south and 40° of longitude east and west of a central meridian.
| φ | Values of x and y. | ||||
| ω = 0° | ω = 10° | ω = 20° | ω = 30° | ω = 40° | |
| 0° | x = 0.00 | 9.69 | 19.43 | 29.25 | 39.17 |
| y = 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 10° | x = 0.00 | 9.60 | 19.24 | 28.95 | 38.76 |
| y = 9.69 | 9.75 | 9.92 | 10.21 | 10.63 | |
| 20° | x = 0.00 | 9.32 | 18.67 | 28.07 | 37.53 |
| y = 19.43 | 19.54 | 19.87 | 20.43 | 21.25 | |
| 30° | x = 0.00 | 8.84 | 17.70 | 26.56 | 35.44 |
| y = 29.25 | 29.40 | 29.87 | 30.67 | 31.83 | |
| 40° | x = 0.00 | 8.15 | 16.28 | 24.39 | 32.44 |
| y = 39.17 | 39.36 | 39.94 | 40.93 | 42.34 | |
 |
| Fig. 13. |
Central or Gnomonic (Perspective) Projection.—In this projection the eye is imagined to be at the centre of the sphere. It is evident that, since the planes of all great circles of the sphere pass through the centre, the representations of all great circles on this projection will be straight lines, and this is the special property of the central projection, that any great circle (i.e. shortest line on the spherical surface) is represented by a straight line. The plane of projection may be either parallel to the plane of the equator, in which case the parallels are represented by concentric circles and the meridians by straight lines radiating from the common centre; or the plane of projection may be parallel to the plane of some meridian, in which case the meridians are parallel straight lines and the parallels are hyperbolas; or the plane of projection may be inclined to the axis of the sphere at any angle λ.
In the latter case, which is the most general, if θ is the angle any meridian makes (on paper) with the central meridian, α the longitude of any point P with reference to the central meridian, l the latitude of P, then it is clear that the central meridian is a straight line at right angles to the equator, which is also a straight line, also tan θ = sin λ tan α, and the distance of p, the projection of P, from the equator along its meridian is (on paper) m sec α sin l / sin (l + x), where tan x = cot λ cos α, and m is a constant which defines the scale.
The three varieties of the central projection are, as is the case with other perspective projections, known as polar, meridian or horizontal, according to the inclination of the plane of projection.
Fig. 14 is an example of a meridian central projection of part of the Atlantic Ocean. The term “gnomonic” was applied to this projection because the projection of the meridians is a similar problem to that of the graduation of a sun-dial. It is, however, better to use the term “central,” which explains itself. The central projection is useful for the study of direct routes by sea and land. The United States Hydrographic Department has published some charts on this projection. False notions of the direction of shortest lines, which are engendered by a study of maps on Mercator’s projection, may be corrected by an inspection of maps drawn on the central projection.
There is no projection which accurately possesses the property of showing shortest paths by straight lines when applied to the spheroid; one which very nearly does so is that which results from the intersection of terrestrial normals with a plane.
We have briefly reviewed the most important projections which are derived from the sphere by direct geometrical construction, and we pass to that more important branch of the subject which deals with projections which are not subject to this limitation.
Conical Projections.
Conical projections are those in which the parallels are represented by concentric circles and the meridians by equally spaced radii. There is no necessary connexion between a conical projection and any touching or secant cone. Projections for instance which are derived by geometrical construction from secant cones are very poor projections, exhibiting large errors, and they will not be discussed. The name conical is given to the group embraced by the above definition, because, as is obvious, a projection so drawn can be bent round to form a cone. The simplest and, at the same time, one of the most useful forms of conical projection is the following:
 |
| Fig. 15. |
Conical Projection with Rectified Meridians and Two Standard Parallels.—In some books this has been, most unfortunately, termed the “secant conical,” on account of the fact that there are two parallels of the correct length. The use of this term in the past has caused much confusion. Two selected parallels are represented by concentric circular arcs of their true lengths; the meridians are their radii. The degrees along the meridians are represented by their true lengths; and the other parallels are circular arcs through points so determined and are concentric with the chosen parallels.
Thus in fig. 15 two parallels Gn and G′n′ are represented by their true lengths on the sphere; all the distances along the meridian PGG′, pnn′ are the true spherical lengths rectified.
Let γ be the co-latitude of Gn; γ′ that of Gn′; ω be the true difference of longitude of PGG′ and pnn′; hω be the angle at O; and OP = z, where Pp is the representation of the pole. Then the true length of parallel Gn on the sphere is ω sin γ, and this is equal to the length on the projection, i.e. ω sin γ = hω (z + γ); similarly ω sin γ′ = hω (z + γ′).
The radius of the sphere is assumed to be unity, and z and γ are expressed in circular measure. Hence h = sin γ/(z + γ) = sin γ′ (z + γ′); from this h and z are easily found.
In the above description it has been assumed that the two errorless parallels have been selected. But it is usually desirable to impose some condition which itself will fix the errorless parallels. There are many conditions, any one of which may be imposed. In fig. 15 let Cm and C′m′ represent the extreme parallels of the map, and let the co-latitudes of these parallels be c and c′, then any one of the following conditions may be fulfilled:—
(a) The errors of scale of the extreme parallels may be made equal and may be equated to the error of scale of the parallel of maximum error (which is near the mean parallel).
(b) Or the errors of scale of the extreme parallels may be equated to that of the mean parallel. This is not so good a projection as (a).
(c) Or the absolute errors of the extreme and mean parallels may be equated.
(d) Or in the last the parallel of maximum error may be considered instead of the mean parallel.
(e) Or the mean length of all the parallels may be made correct. This is equivalent to making the total area between the extreme parallels correct, and must be combined with another condition, for example, that the errors of scale on the extreme parallels shall be equal.
We will now discuss (a) above, viz. a conical projection with rectified meridians and two standard parallels, the scale errors of the extreme parallels and parallel of maximum error being equated.
Since the scale errors of the extreme parallels are to be equal,
| h (z + c) | − 1 = | h (z + c′) | − 1, whence z = | c′ sin c − c sin c′ | . |
| sin c | sin c′ | sin c′ − sin c |
The error of scale along any parallel (near the centre), of which the co-latitude is b is
This is a maximum when
Also
| 1 − | h (z + b) | = | h (z + c) | − 1 whence h is found. |
| sin b | sin c |
For the errorless parallels of co-latitudes γ and γ′ we have
If this is applied to the case of a map of South Africa between the limits 15° S. and 35° S. (see fig. 16) it will be found that the parallel of maximum error is 25° 20′; the errorless parallels, to the nearest degree, are those of 18° and 32°. The greatest scale error in this case is about 0.7%.
In the above account the earth has been treated as a sphere. Of course its real shape is approximately a spheroid of revolution, and the values of the axes most commonly employed are those of Clarke or of Bessel. For the spheroid, formulae arrived at by the same principles but more cumbrous in shape must be used. But it will usually be sufficient for the selection of the errorless parallels to use the simple spherical formulae given above; then, having made the selection of these parallels, the true spheroidal lengths along the meridians between them can be taken out of the ordinary tables (such as those published by the Ordnance Survey or by the U.S. Coast and Geodetic Survey). Thus, if a1, a2, are the lengths of 1° of the errorless parallels (taken from the tables), d the true rectified length of the meridian arc between them (taken from the tables),
and the radius on paper of parallel, a1 is a1d/(a2 − a1), and the radius of any other parallel = radius of a1 ± the true meridian distance between the parallels.
This class of projection was used for the 1/1,000,000 Ordnance map of the British Isles. The three maximum scale errors in this case work out to 0.23%, the range of the projection being from 50° N. to 61° N., and the errorless parallels are 59° 31′ and 51°44′.
Where no great refinement is required it will be sufficient to take the errorless parallels as those distant from the extreme parallels about one-sixth of the total range in latitude. Thus suppose it is required to plot a projection for India between latitudes 8° and 40° N. By this rough rule the errorless parallels should be distant from the extreme parallels about 32°/6, i.e. 5° 20′; they should therefore, to the nearest degree, be 13° and 35° N. The maximum scale errors will be about 2%.
The scale errors vary approximately as the square of the range of latitude; a rough rule is, largest scale error = L2/50,000, where L is the range in the latitude in degrees. Thus a country with a range of 7° in latitude (nearly 500 m.) can be plotted on this projection with a maximum linear scale error (along a parallel) of about 0.1%;[29] there is no error along any meridian. It is immaterial with this projection (or with any conical projection) what the extent in longitude is. It is clear that this class of projection is accurate, simple and useful.
In the projections designated by (c) and (d) above, absolute errors of length are considered in the place of errors of scale, i.e. between any two meridians (c) the absolute errors of length of the extreme parallels are equated to the absolute error of length of the middle parallel. Using the same notation
L. Euler, in the Acta Acad. Imp. Petrop. (1778), first discussed this projection.
If a map of Asia between parallels 10° N. and 70° N. is constructed on this system, we have c = 20°, c′ = 80°, whence from the above equations z = 66.7° and h = .6138. The absolute errors of length along parallels 10°, 40° and 70° between any two meridians are equal but the scale errors are respectively 5, 6.7, and 15%.
The modification (d) of this projection was selected for the 1:1,000,000 map of India and Adjacent Countries under publication by the Survey of India. An account of this is given in a pamphlet produced by that department in 1903. The limiting parallels are 8° and 40° N., and the parallel of greatest error is 23° 40′ 51″. The errors of scale are 1.8, 2.3, and 1.9%.
It is not as a rule desirable to select this form of the projection. If the surface of the map is everywhere equally valuable it is clear that an arrangement by which errors of scale are larger towards the pole than towards the equator is unsound, and it is to be noted that in the case quoted the great bulk of the land is in the north of the map. Projection (a) would for the same region have three equal maximum scale errors of 2%. It may be admitted that the practical difference between the two forms is in this case insignificant, but linear scale errors should be reduced as much as possible in maps intended for general use.
f. In the fifth form of the projection, the total area of the projection between the extreme parallels and any two meridians is equated to the area of the portion of the sphere which it represents, and the errors of scale of the extreme parallels are equated. Then it is easy to show that
| z = (c′ sin c − c sin c′) / (sin c′ − sin c); |
| h = (cos c − cos c′) / (c′ − c) {z + 12 (c + c′)}. |
It can also be shown that any other zone of the same range in latitude will have the same scale errors along its limiting parallels. For instance, a series of projections may be constructed for zones, each having a range of 10° of latitude, from the equator to the pole. Treating the earth as a sphere and using the above formulae, the series will possess the following properties: the meridians will all be true to scale, the area of each zone will be correct, the scale errors of the limiting parallels will all be the same, so that the length of the upper parallel of any zone will be equal to that of the lower parallel of the zone above it. But the curvatures of these parallels will be different, and two adjacent zones will not fit but will be capable of exact rolling contact. Thus a very instructive flat model of the globe may be constructed which will show by suitably arranging the points of contact of the zones the paths of great circles on the sphere. The flat model was devised by Professor J. D. Everett, F.R.S., who also pointed out that the projection had the property of the equality of scale errors of the limiting parallels for zones of the same width. The projection may be termed Everett’s Projection.
Simple Conical Projection.—If in the last group of projections the two selected parallels which are to be errorless approach each other indefinitely closely, we get a projection in which all the meridians are, as before, of the true rectified lengths, in which one parallel is errorless, the curvature of that parallel being clearly that which would result from the unrolling of a cone touching the sphere along the parallel represented. And it was in fact originally by a consideration of the tangent cone that the whole group of conical projections came into being. The quasi-geometrical way of regarding conical projections is legitimate in this instance.
 |
| Fig. 17. |
The simple conical projection is therefore arrived at in this way: imagine a cone to touch the sphere along any selected parallel, the radius of this parallel on paper (Pp, fig. 17) will be r cot φ, where r is the radius of the sphere and φ is the latitude; or if the spheroidal shape is taken into account, the radius of the parallel on paper will be ν cot φ where ν is the normal terminated by the minor axis (the value ν can be found from ordinary geodetic tables). The meridians are generators of the cone and every parallel such as HH′ is a circle, concentric with the selected parallel Pp and distant from it the true rectified length of the meridian arc between them.
This projection has no merits as compared with the group just described. The errors of scale along the parallels increase rapidly as the selected parallel is departed from, the parallels on paper being always too large. As an example we may take the case of a map of South Africa of the same range as that of the example given in (a) above, viz. from 15° S. to 35° S. Let the selected parallel be 25° S.; the radius of this parallel on paper (taking the radius of the sphere as unity) is cot 25°; the radius of parallel 35° S. = radius of 25° − meridian distance between 25° and 35° = cot 25° − 10π/180 = 1.970. Also h = sin of selected latitude = sin 25°, and length on paper along parallel 35° of ω° = ωh× 1.970 = ω × 1.970 × sin 25°,
| hence scale error = | 1.970 sin 25° | − 1 = 1.6%, |
| cos 35° |
an error which is more than twice as great as that obtained by method (a).
Bonne’s Projection.—This projection, which is also called the “modified conical projection,” is derived from the simple conical, just described, in the following way: a central meridian is chosen and drawn as a straight line; degrees of latitude spaced at the true rectified distances are marked along this line; the parallels are concentric circular arcs drawn through the proper points on the central meridian, the centre of the arcs being fixed by describing one chosen parallel with a radius of ν cot φ as before; the meridians on each side of the central meridian are drawn as follows: along each parallel distances are marked equal to the true lengths along the parallels on sphere or spheroid, and the curve through corresponding points so fixed are the meridians (fig. 18).
 |
| Fig. 18. |
This system is that which was adopted in 1803 by the “Dépôt de la Guerre” for the map of France, and is there known by the title of Projection de Bonne. It is that on which the ordnance survey map of Scotland on the scale of 1 in. to a mile is constructed, and it is frequently met with in ordinary atlases. It is ill-adapted for countries having great extent in longitude, as the intersections of the meridians and parallels become very oblique—as will be seen on examining the map of Asia in most atlases.
If φ0 be taken as the latitude of the centre parallel, and co-ordinates be measured from the intersection of this parallel with the central meridian, then, if ρ be the radius of the parallel of latitude φ, we have ρ = cot φ0 + φ0 − φ. Also, if S be a point on this parallel whose co-ordinates are x, y, so that VS = ρ, and θ be the angle VS makes with the central meridian, then ρθ = ω cos φ; and x = ρ sin θ, y = cot φ0 − ρ cos θ.
The projection has the property of equal areas, since each small element bounded by two infinitely close parallels is equal in length and width to the corresponding element on the sphere or spheroid. Also all the meridians cross the chosen parallel (but no other) at right angles, since in the immediate neighbourhood of that parallel the projection is identical with the simple conical projection. Where an equal-area projection is required for a country having no great extent in longitude, such as France, Scotland or Madagascar, this projection is a good one to select.
 |
| Fig. 19.—Sinusoidal Equal-area Projection. |
Sinusoidal Equal-area Projection.—This projection, which is sometimes known as Sanson’s, and is also sometimes incorrectly called Flamsteed’s, is a particular case of Bonne’s in which the selected parallel is the equator. The equator is a straight line at right angles to the central meridian which is also a straight line. Along the central meridian the latitudes are marked off at the true rectified distances, and from points so found the parallels are drawn as straight lines parallel to the equator, and therefore at right angles to the central meridian. True rectified lengths are marked along the parallels and through corresponding points the meridians are drawn. If the earth is treated as a sphere the meridians are clearly sine curves, and for this reason d’Avezac has given the projection the name sinusoidal. But it is equally easy to plot the spheroidal lengths. It is a very suitable projection for an equal-area map of Africa.
Werner’s Projection.—This is another limiting case of Bonne’s equal-area projection in which the selected parallel is the pole. The parallels on paper then become incomplete circular arcs of which the pole is the centre. The central meridian is still a straight line which is cut by the parallels at true distances. The projection (after Johann Werner, 1468–1528), though interesting, is practically useless.
Polyconic Projections.
These pseudo-conical projections are valuable not so much for their intrinsic merits as for the fact that they lend themselves to tabulation. There are two forms, the simple or equidistant polyconic, and the rectangular polyconic.
The Simple Polyconic.—If a cone touches the sphere or spheroid along a parallel of latitude φ and is then unrolled, the parallel will on paper have a radius of ν cot φ, where ν is the normal terminated by the minor axis. If we imagine a series of cones, each of which touches one of a selected series of parallels, the apex of each cone will lie on the prolonged axis of the spheroid; the generators of each cone lie in meridian planes, and if each cone is unrolled and the generators in any one plane are superposed to form a straight central meridian, we obtain a projection in which the central meridian is a straight line and the parallels are circular arcs each of which has a different centre which lies on the prolongation of the central meridian, the radius of any parallel being ν cot φ.
So far the construction is the same for both forms of polyconic. In the simple polyconic the meridians are obtained by measuring outwards from the central meridian along each parallel the true lengths of the degrees of longitude. Through corresponding points so found the meridian curves are drawn. The resulting projection is accurate near the central meridian, but as this is departed from the parallels increasingly separate from each other, and the parallels and meridians (except along the equator) intersect at angles which increasingly differ from a right angle. The real merit of the projection is that each particular parallel has for every map the same absolute radius, and it is thus easy to construct tables which shall be of universal use. This is especially valuable for the projection of single sheets on comparatively large scales. A sheet of a degree square on a scale of 1:250,000 projected in this manner differs inappreciably from the same sheet projected on a better system, e.g. an orthomorphic conical projection or the conical with rectified meridians and two standard parallels; there is thus the advantage that the simple polyconic when used for single sheets and large scales is a sufficiently close approximation to the better forms of conical projection. The simple polyconic is used by the topographical section of the general staff, by the United States coast and geodetic survey and by the topographical division of the U.S. geological survey. Useful tables, based on Clarke’s spheroid of 1866, have been published by the war office and by the U.S. coast and geodetic survey.
 |
| Fig. 20. |
Rectangular Polyconic.—In this the central meridian and the parallels are drawn as in the simple polyconic, but the meridians are curves which cut the parallels at right angles.
In this case, let P (fig. 20) be the north pole, CPU the central meridian, U, U′ points in that meridian whose co-latitudes are z and z+dz, so that UU′ = dz. Make PU = z, UC = tan z, U′C′ = tan (z + dz); and with CC′ as centres describe the arcs UQ, U′Q′, which represent the parallels of co-latitude z and z + dz. Let PQQ′ be part of a meridian curve cutting the parallels at right angles. Join CQ, C′Q′; these being perpendicular to the circles will be tangents to the curve. Let UCQ = 2α, UC′Q′ = 2(α + dα), then the small angle CQC′, or the angle between the tangents at QQ′, will = 2dα. Now
The tangents CQ, C′Q′ will intersect at q, and in the triangle CC′q the perpendicular from C on C′q is (omitting small quantities of the second order) equal to either side of the equation
−tan zdz = 2 dα / sin 2α,
which is the differential equation of the meridian: the integral is tan α = ω cos z, where ω, a constant, determines a particular meridian curve. The distance of Q from the central meridian, tan z sin 2α, is equal to
| 2 tan z tan α | = | 2ω sin z | . |
| 1 + tan2 α | 1 + ω2 cos2 α |
 |
| Fig. 21. |
At the equator this becomes simply 2ω. Let any equatorial point whose actual longitude is 2ω be represented by a point on the developed equator at the distance 2ω from the central meridian, then we have the following very simple construction (due to O’Farrell of the ordnance survey). Let P (fig. 21) be the pole, U any point in the central meridian, QUQ′ the represented parallel whose radius CU = tan z. Draw SUS′ perpendicular to the meridian through U; then to determine the point Q, whose longitude is, say, 3°, lay off US equal to half the true length of the arc of parallel on the sphere, i.e. 1° 30′ to radius sin z, and with the centre S and radius SU describe a circular arc, which will intersect the parallel in the required point Q. For if we suppose 2ω to be the longitude of the required point Q, US is by construction = ω sin z, and the angle subtended by SU at C is
| tan−1 ( | ω sin z | ) = tan−1 (ω cos z) = α, |
| tan z |
and therefore UCQ = 2α as it should be. The advantages of this method are that with a remarkably simple and convenient mode of construction we have a map in which the parallels and meridians intersect at right angles.
 |
| Fig. 22. |
Fig. 22 is a representation of this system of the continents of Europe and Africa, for which it is well suited. For Asia this system would not do, as in the northern latitudes, say along the parallel of 70°, the representation is much cramped.
With regard to the distortion in the map of Africa as thus constructed, consider a small square in latitude 40° and in 40° longitude east or west of the central meridian, the square being so placed as to be transformed into a rectangle. The sides, originally unity, became 0.95 and 1.13, and the area 1.08, the diagonals intersecting at 90° ± 9° 56′. In Clarke’s perspective projection a square of unit side occupying the same position, when transformed to a rectangle, has its sides 1.02 and 1.15, its area 1.17, and its diagonals intersect at 90° ± 7° 6′. The latter projection is therefore the best in point of “similarity,” but the former represents areas best. This applies, however, only to a particular part of the map; along the equator towards 30° or 40° longitude, the polyconic is certainly inferior, while along the meridian it is better than the perspective—except, of course, near the centre. Upon the whole the more even distribution of distortion gives the advantage to the perspective system. For single sheets on large scales there is nothing to choose between this projection and the simple polyconic. Both are sensibly perfect representations. The rectangular polyconic is occasionally used by the topographical section of the general staff.
Zenithal Projections.
Some point on the earth is selected as the central point of the map; great circles radiating from this point are represented by straight lines which are inclined at their true angles at the point of intersection. Distances along the radiating lines vary according to any law outwards from the centre. It follows (on the spherical assumption), that circles of which the selected point is the centre are also circles on the projection. It is obvious that all perspective projections are zenithal.
Equidistant Zenithal Projection.—In this projection, which is commonly called the “equidistant projection,” any point on the sphere being taken as the centre of the map, great circles through this point are represented by straight lines of the true rectified lengths, and intersect each other at the true angles.
In the general case—
if z1 is the co-latitude of the centre of the map, z the co-latitude of any other point, α the difference of longitude of the two points, A the azimuth of the line joining them, and c the spherical length of the line joining them, then the position of the intersection of any meridian with any parallel is given (on the spherical assumption) by the solution of a simple spherical triangle.
Thus—
let tan θ = tan z cos α, then cos c = cos z sec θ cos (z − θ), and sin A = sin z sin α cosec c.
The most useful case is that in which the central point is the pole; the meridians are straight lines inclined to each other at the true angular differences of longitude, and the parallels are equidistant circles with the pole as centre. This is the best projection to use for maps exhibiting the progress of polar discovery, and is called the polar equidistant projection. The errors are smaller than might be supposed. There are no scale errors along the meridians, and along the parallels the scale error is (z / sin x) − 1, where z is the co-latitude of the parallel. On a parallel 10° distant from the pole the error of scale is only 0.5%.
General Theory of Zenithal Projections.—For the sake of simplicity it will be at first assumed that the pole is the centre of the map, and that the earth is a sphere. According to what has been said above, the meridians are now straight lines diverging from the pole, dividing the 360° into equal angles; and the parallels are represented by circles having the pole as centre, the radius of the parallel whose co-latitude is z being ρ, a certain function of z. The particular function selected determines the nature of the projection.
 |
| Fig. 23. |
Let Ppq, Prs (fig. 23) be two contiguous meridians crossed by parallels rp, sq, and Op′q′, Or ′s′ the straight lines representing these meridians. If the angle at P is dμ, this also is the value of the angle at O. Let the co-latitude
the circular arcs p′r ′, q′s′ representing the parallels pr, qs. If the radius of the sphere be unity,
pq = dz; pr = sin z dμ.
Put
then p′q′ = σpq and p′r ′ = σ′pr. That is to say, σ, σ′ may be regarded as the relative scales, at co-latitude z, of the representation, σ applying to meridional measurements, σ′ to measurements perpendicular to the meridian. A small square situated in co-latitude z, having one side in the direction of the meridian—the length of its side being i—is represented by a rectangle whose sides are iσ and iσ′; its area consequently is i2σσ′.
If it were possible to make a perfect representation, then we should have σ = 1, σ′ = 1 throughout. This, however, is impossible. We may make σ = 1 throughout by taking ρ = z. This is the Equidistant Projection just described, a very simple and effective method of representation.
Or we may make σ′= 1 throughout. This gives ρ = sin z, a perspective projection, namely, the Orthographic.
Or we may require that areas be strictly represented in the development. This will be effected by making σσ′ = 1, or ρ dρ = sin zdz, the integral of which is ρ = 2 sin 12z, which is the Zenithal Equal-area Projection of Lambert, sometimes, though wrongly referred to as Lorgna’s Projection after Antonio Lorgna (b. 1736). In this system there is misrepresentation of form, but no misrepresentation of areas.
Or we may require a projection in which all small parts are to be represented in their true forms i.e. an orthomorphic projection. For instance, a small square on the spherical surface is to be represented as a small square in the development. This condition will be attained by making σ = σ′, or dρ/ρ = dz/sin z, the integral of which is, c being an arbitrary constant, ρ = c tan 12z. This, again, is a perspective projection, namely, the Stereographic. In this, though all small parts of the surface are represented in their correct shapes, yet, the scale varying from one part of the map to another, the whole is not a similar representation of the original. The scale, σ = 12c sec2 12z, at any point, applies to all directions round that point.
These two last projections are, as it were, at the extremes of the scale; each, perfect in its own way, is in other respects objectionable. We may avoid both extremes by the following considerations. Although we cannot make σ = 1 and σ′ = 1, so as to have a perfect picture of the spherical surface, yet considering σ − 1 and σ′ − 1 as the local errors of the representation, we may make (σ − 1)2 + (σ′ − 1)2 a minimum over the whole surface to be represented. To effect this we must multiply this expression by the element of surface to which it applies, viz. sin zd zd μ, and then integrate from the centre to the (circular) limits of the map. Let β be the spherical radius of the segment to be represented, then the total misrepresentation is to be taken as
| ∫β0 { ( | dρ | − 1 )2 + ( | ρ | − 1 )2 } sin zdz, |
| dz | sin z |
which is to be made a minimum. Putting ρ = z + y, and giving to y only a variation subject to the condition δy = 0 when z = 0, the equations of solution—using the ordinary notation of the calculus of variations—are
| N − | d(P) | = 0; Pβ = 0, |
| dz |
Pβ being the value of 2p sin z when z = β. This gives
| sin2 z | d2y | + sin z cos z | dy | − y = z − sin z ( | dy | ) β = 0. |
| dz2 | dz | dz |
This method of development is due to Sir George Airy, whose original paper—the investigation is different in form from the above, which is due to Colonel Clarke—will be found in the Philosophical Magazine for 1861. The solution of the differential equation leads to this result—
| ρ = 2 cot 12z loge sec 12z + C tan 12z, |
| C = 2 cot2 12β loge sec 12β. |
The limiting radius of the map is R = 2C tan 12β. In this system, called by Sir George Airy Projection by balance of errors, the total misrepresentation is an absolute minimum. For short it may be called Airy’s Projection.
Returning to the general case where ρ is any function of z, let us consider the local misrepresentation of direction. Take any indefinitely small line, length = i, making an angle α with the meridian in co-latitude z. Its projections on a meridian and parallel are i cos α, i sin α, which in the map are represented by iσ cos α, iσ′ sin α. If then α′ be the angle in the map corresponding to α,
Put
and the error α′ − α of representation = ε, then
| tan ε = | (Σ − 1) tan α | . |
| 1 + Σ tan2 α |
Put Σ = cot2 ζ, then ε is a maximum when α = ζ, and the corresponding value of ε is
For simplicity of explanation we have supposed this method of development so applied as to have the pole in the centre. There is, however, no necessity for this, and any point on the surface of the sphere may be taken as the centre. All that is necessary is to calculate by spherical trigonometry the azimuth and distance, with reference to the assumed centre, of all the points of intersection of meridians and parallels within the space which is to be represented in a plane. Then the azimuth is represented unaltered, and any spherical distance z is represented by ρ. Thus we get all the points of intersection transferred to the representation, and it remains merely to draw continuous lines through these points, which lines will be the meridians and parallels in the representation.
Thus treating the earth as a sphere and applying the Zenithal Equal-area Projection to the case of Africa, the central point selected being on the equator, we have, if θ be the spherical distance of any point from the centre, φ, α the latitude and longitude (with reference to the centre), of this point, cos θ = cos φ cos α. If A is the azimuth of this point at the centre, tan A = sin α cot φ. On paper a line from the centre is drawn at an azimuth A, and the distance θ is represented by 2 sin 12θ. This makes a very good projection for a single-sheet equal-area map of Africa. The exaggeration in such systems, it is important to remember, whether of linear scale, area, or angle, is the same for a given distance from the centre, whatever be the azimuth; that is, the exaggeration is a function of the distance from the centre only.
General Theory of Conical Projections.
 |
| Fig. 24. |
Meridians are represented by straight lines drawn through a point, and a difference of longitude ω is represented by an angle hω. The parallels of latitude are circular arcs, all having as centre the point of divergence of the meridian lines. It is clear that perspective and zenithal projections are particular groups of conical projections.
Let z be the co-latitude of a parallel, and ρ, a function of z, the radius of the circle representing this parallel. Consider the infinitely small space on the sphere contained by two consecutive meridians, the difference of whose longitude is dμ, and two consecutive parallels whose co-latitudes are z and z + dz. The sides of this rectangle are pq = dz, pr = sin zdμ; in the projection p′q′r′s′ these become p′q′ = dρ, and p′r′ = ρhdμ.
The scales of the projection as compared with the sphere are p′q′/pq = dρ/dz = the scale of meridian measurements = σ, say, and p′r′/pr = ρhdμ/sin zdμ = ρh/sin z = scale of measurements perpendicular to the meridian = σ′, say.
Now we may make σ = 1 throughout, then ρ = z + const. This gives either the group of conical projections with rectified meridians, or as a particular case the equidistant zenithal.
We may make σ = σ′ throughout, which is the same as requiring that at any point the scale shall be the same in all directions. This gives a group of orthomorphic projections.
In this case dρ/dz = ρh/sin z, or dρ/ρ = hdz/sin z.
Integrating,
where k is a constant.
Now h is at our disposal and we may give it such a value that two selected parallels are of the correct lengths. Let z1, z2 be the co-latitudes of these parallels, then it is easy to show that
| h = | log sin z1 − log sin z2 | . |
| log tan 12z1 − log tan 12z2 |
This projection, given by equations (i.) and (ii.), is Lambert’s
orthomorphic projection—commonly called Gauss’s projection;
its descriptive name is the orthomorphic conical projection with two
standard parallels.
The constant k in (i.) defines the scale and may be used to render the scale errors along the selected parallels not nil but the same; and some other parallel, e.g. the central parallel may then be made errorless.
The value h = 13, as suggested by Sir John Herschel, is admirably suited for a map of the world. The representation is fan-shaped, with remarkably little distortion (fig. 24).
If any parallel of co-latitude z is true to scale hk(tan 12z1)h = sin z, if this parallel is the equator, so that z1 = 90°, kh = 1, then equation (i.) becomes ρ = (tan 12z)h/h, and the radius of the equator = 1/h. The distance r of any parallel from the equator is 1/h − (tan 12z)h/h = (1/h){1 − (tan 12z)h}.
If, instead of taking the radius of the earth as unity we call it a, r = (a/h){1 − (tan 12z)h}. When h is very small, the angles between the meridian lines in the representation are very small; and proceeding to the limit, when h is zero the meridians are parallel—that is, the vertex of the cone has removed to infinity. And at the limit when h is zero we have r = a loge cot 12z, which is the characteristic equation of Mercator’s projection.
 |
| Fig. 25.—Elliptical equal-area Projection, showing the whole surface of the globe. |
Mercator’s Projection.—From the manner in which we have arrived at this projection it is clear that it retains the characteristic property of orthomorphic projections—namely, similarity of representation of small parts of the surface. In Mercator’s chart the equator is represented by a straight line, which is crossed at right angles by a system of parallel and equidistant straight lines representing the meridians. The parallels are straight lines parallel to the equator, and the distance of the parallel of latitude φ from the equator is, as we have seen above, r = a loge tan (45° + 12φ). In the vicinity of the equator, or indeed within 30° of latitude of the equator, the representation is very accurate, but as we proceed northwards or southwards the exaggeration of area becomes larger, and eventually excessive—the poles being at infinity. This distance of the parallels may be expressed in the form r = a (sin φ + 13 sin3 φ + 15 sin5 φ + . . .), showing that near the equator r is nearly proportional to the latitude. As a consequence of the similar representation of small parts, a curve drawn on the sphere cutting all meridians at the same angle—the loxodromic curve—is projected into a straight line, and it is this property which renders Mercator’s chart so valuable to seamen. For instance: join by a straight line on the chart Land’s End and Bermuda, and measure the angle of intersection of this line with the meridian. We get thus the bearing which a ship has to retain during its course between these ports. This is not great-circle sailing, and the ship so navigated does not take the shortest path. The projection of a great circle (being neither a meridian nor the equator) is a curve which cannot be represented by a simple algebraic equation.
If the true spheroidal shape of the earth is considered, the semiaxes being a and b, putting e = √(a2 − b2) / a, and using common logarithms, the distance of any parallel from the equator can be shown to be
where M, the modulus of common logarithms, = 0.434294. Of course Mercator’s projection was not originally arrived at in the manner above described; the description has been given to show that Mercator’s projection is a particular case of the conical orthomorphic group. The introduction of the projection is due to the fact that for navigation it is very desirable to possess charts which shall give correct local outlines (i.e. in modern phraseology shall be orthomorphic) and shall at the same time show as a straight line any line which cuts the meridians at a constant angle. The latter condition clearly necessitates parallel meridians, and the former a continuous increase of scale as the equator is departed from, i.e. the scale at any point must be equal to the scale at the equator × sec. latitude. In early days the calculations were made by assuming that for a small increase of latitude, say 1′, the scale was constant, then summing up the small lengths so obtained. Nowadays (for simplicity the earth will be taken as a sphere) we should say that a small length of meridian adφ is represented in this projection by a sec φ dφ, and the length of the meridian in the projection between the equator and latitude φ,
which is the direct way of arriving at the law of the construction
Mercator’s projection, although indispensable at sea, is of little value for land maps. For topographical sheets it is obviously unsuitable; and in cases in which it is required to show large areas on small scales on an orthomorphic projection, that form should be chosen which gives two standard parallels (Lambert’s conical orthomorphic). Mercator’s projection is often used in atlases for maps of the world. It is not a good projection to select for this purpose on account of the great exaggeration of scale near the poles. The misconceptions arising from this exaggeration of scale may, however, be corrected by the juxtaposition of a map of the world on an equal-area projection.
It is now necessary to revert to the general consideration of conical projections.
It has been shown that the scales of the projection (fig. 23) as compared with the sphere are p′q′ / pq = dp / dz = σ along a meridian, and p′r ′ / pr ′ = ρh/ sin z = σ′ at right angles to a meridian.
Now if σσ′ = 1 the areas are correctly represented, then
this gives the whole group of equal-area conical projections.
As a special case let the pole be the centre of the projected parallels, then when
Let z1 be the co-latitude of some parallel which is to be correctly represented, then 2h sin 12z1 / δh= sin z1, and h = cos2 12z1; putting this value of h in equation (ii.) the radius of any parallel
This is Lambert’s conical equal-area projection with one standard parallel, the pole being the centre of the parallels.
If we put z1=θ, then h = 1, and the meridians are inclined at their true angles, also the scale at the pole becomes correct, and equation (iii.) becomes
this is the zenithal equal-area projection.
Reverting to the general expression for equal-area conical projections
we can dispose of C and h so that any two selected parallels shall be their true lengths; let their co-latitudes be z1 and z2, then
from which C and h are easily found, and the radii are obtained from (i.) above. This is H. C. Albers’ conical equal-area projection with two standard parallels. The pole is not the centre of the parallels.
Projection by Rectangular Spheroidal Co-ordinates.
If in the simple conical projection the selected parallel is the equator, this and the other parallels become parallel straight lines and the meridians are straight lines spaced at equatorial distances, cutting the parallels at right angles; the parallels are their true distances apart. This projection is the simple cylindrical. If now we imagine the touching cylinder turned through a right-angle In such a way as to touch the sphere along any meridian, a projection is obtained exactly similar to the last, except that in this case we represent, not parallels and meridians, but small circles parallel to the given meridian and great circles at right angles to it. It is clear that the projection is a special case of conical projection. The position of any point on the earth’s surface is thus referred, on this projection, to a selected meridian as one axis, and any great circle at right angles to it as the other. Or, in other words, any point is fixed by the length of the perpendicular from it on to the fixed meridian and the distance of the foot of the perpendicular from some fixed point on the meridian, these spherical or spheroidal co-ordinates being plotted as plane rectangular co-ordinates.
The perpendicular is really a plane section of the surface through the given point at right angles to the chosen meridian, and may be briefly called a great circle. Such a great circle clearly diverges from the parallel; the exact difference in latitude and longitude between the point and the foot of the perpendicular can be at once obtained by ordinary geodetic formulae, putting the azimuth = 90°. Approximately the difference of latitude in seconds is x2 tan φ cosec 1″ / 2ρν where x is the length of the perpendicular, ρ that of the radius of curvature to the meridian, ν that of the normal terminated by the minor axis, φ the latitude of the foot of the perpendicular. The difference of longitude in seconds is approximately x sec ρ cosec 1″ / ν. The resulting error consists principally of an exaggeration of scale north and south and is approximately equal to sec x (expressing x in arc); it is practically independent of the extent in latitude.
It is on this projection that the 1/2,500 Ordnance maps and the 6-in. Ordnance maps of the United Kingdom are plotted, a meridian being chosen for a group of counties. It is also used for the 1-in., 12 in. and 14 in. Ordnance maps of England, the central meridian chosen being that which passes through a point in Delamere Forest in Cheshire. This projection should not as a rule be used for topographical maps, but is suitable for cadastral plans on account of the convenience of plotting the rectangular co-ordinates of the very numerous trigonometrical or traverse points required in the construction of such plans. As regards the errors involved, a range of about 150 miles each side of the central meridian will give a maximum error in scale in a north and south direction of about 0.1%.
Elliptical Equal-area Projection.
In this projection, which is also called Mollweide’s projection the parallels are parallel straight lines and the meridians are ellipses, the central meridian being a straight line at right angles to the equator, which is equally divided. If the whole world is represented on the spherical assumption, the equator is twice the length of the central meridian. Each elliptical meridian has for one axis the central meridian, and for the other the intercepted portion of the equally divided equator. It follows that the meridians 90° east and west of the central meridian form a circle. It is easy to show that to preserve the property of equal areas the distance of any parallel from the equator must be √2 sin δ where π sin φ = 2δ + sin 2δ, φ being the latitude of the parallel. The length of the central meridian from pole to pole = 2 √2, where the radius of the sphere is unity. The length of the equator = 4 √2.
The following equal-area projections may be used to exhibit the entire surface of the globe: Cylindrical equal area, Sinusoidal equal area and Elliptical equal area.
 |
| Fig. 26.—Globular Projection. |
Conventional or Arbitrary Projections.
These projections are devised for simplicity of drawing and not for any special properties. The most useful projection of this class is the globular projection. This is a conventional representation of a hemisphere in which the equator and central meridian are two equal straight lines at right angles, their intersection being the centre of the circular boundary. The meridians divide the equator into equal parts and are arcs of circles passing through points so determined and the poles. The parallels are arcs of circles which divide the central and extreme meridians into equal parts. Thus in fig. 26 NS = EW and each is divided into equal parts (in this case each division is 10°); the circumference NESW is also divided into 10° spaces and circular arcs are drawn through the corresponding points. This is a simple and effective projection and one well suited for conveying ideas of the general shape and position of the chief land masses; it is better for this purpose than the stereographic, which is commonly employed in atlases.
 |
| (From Text Book of Topographical Surveying, by permission of the Controller of H.M. Stationery Office.) |
| Fig. 27.—Plane Table Graticule, dimensions in inches, for a scale of 4 in. to 1 m. |
Projections for Field Sheets.
Field sheets for topographical surveys should be on conical projections with rectified meridians; these projections for small areas and ordinary topographical scales—not less than 1/500,000—are sensibly errorless. But to save labour it is customary to employ for this purpose either form of polyconic projection, in which the errors for such scales are also negligible. In some surveys, to avoid the difficulty of plotting the flat arcs required for the parallels, the arcs are replaced by polygons, each side being the length of the portion of the arc it replaces. This method is especially suitable for scales of 1 : 125,000 and larger, but it is also sometimes used for smaller scales.
Fig. 27 shows the method of plotting the projection for a field sheet. Such a projection is usually called a graticule. In this case ABC is the central meridian; the true meridian lengths of 30′ spaces are marked on this meridian, and to each of these, such as AB, the figure (in this case representing a square half degree), such as ABED, is applied. Thus the point D is the intersection of a circle of radius AD with a circle of radius BD, these lengths being taken from geodetic tables. The method has no merit except that of convenience.
Summary.
The following projections have been briefly described:—
| Perspective | 1. Cylindrical equal-area. |
| 2. Orthographic. | |
| 3. Stereographic (which is orthomorphic). | |
| 4. General external perspective. | |
| 5. Minimum error perspective. (Clarke’s). | |
| 6. Central. | |
| Conical | 7. Conical, with rectified meridians and two standard parallels (5 forms). |
| 8. Simple conical. | |
| 9. Simple cylindrical (a special case of 8). | |
| 10. Modified conical equal-area (Bonne’s). | |
| 11. Sinusoidal equal-area (Sanson’s). | |
| 12. Werner’s conical equal-area | |
| 13. Simple polyconic. | |
| 14. Rectangular polyconic. | |
| 15. Conical orthomorphic with 2 standard parallels (Lambert’s, commonly called Gauss’s). | |
| 16. Cylindrical orthomorphic (Mercator’s). | |
| 17. Conical equal-area with one standard parallel. | |
| 18. Conical equal-area with two standard parallels. | |
| 19. Projection by rectangular spheroidal co-ordinates. | |
| Zenithal | 20. Equidistant zenithal. |
| 21. Zenithal equal-area. | |
| 22. Zenithal projection by balance of errors (Airy’s). | |
| 23. Elliptical equal-area (Mollweide’s). | |
| 24. Globular (conventional). | |
| 25. Field sheet graticule. |
Of the above 25 projections, 23 are conical or quasi-conical, if zenithal and perspective projections be included. The projections may, if it is preferred, be grouped according to their properties. Thus in the above list 8 are equal-area, 3 are orthomorphic, 1 balances errors, 1 represents all great circles by straight lines, and in 5 one system of great circles is represented correctly.
Among projections which have not been described may be mentioned the circular orthomorphic (Lagrange’s) and the rectilinear equal-area (Collignon’s) and a considerable number of conventional projections, which latter are for the most part of little value.
The choice of a projection depends on the function which the map is intended to fulfil. If the map is intended for statistical purposes to show areas, density of population, incidence of rainfall, of disease, distribution of wealth, &c., an equal-area projection should be chosen. In such a case an area scale should be given. At sea, Mercator’s is practically the only projection used except when it is desired to determine graphically great circle courses in great oceans, when the central projection must be employed. For conveying good general ideas of the shape and distribution of the surface features of continents or of a hemisphere Clarke’s perspective projection is the best. For exhibiting the progress of polar exploration the polar equidistant projection should be selected. For special maps for general use on scales of 1/1,000,000 and smaller, and for a series of which the sheets are to fit together, the conical, with rectified meridians and two standard parallels, is a good projection. For topographical maps, in which each sheet is plotted independently and the scale is not smaller than 1/500,000, either form of polyconic is very convenient.
The following are the projections adopted for some of the principal official maps of the British Empire:—
Conical, with Rectified Meridians and Two Standard Parallels.—The 1 : 1,000,000 Ordnance map of the United Kingdom, special maps of the topographical section, General Staff, e.g. the 64-mile map of Afghanistan and Persia. The 1 : 1,000,000 Survey of India series of India and adjacent countries.
Modified Conical, Equal-area (Bonne’s).—The 1 in., 12 in., 14 in. and 110 in. Ordnance maps of Scotland and Ireland. The 1 : 800,000 map of the Cape Colony, published by the Surveyor-General.
Simple Polyconic and Rectangular Polyconic maps on scales of 1 : 1,000,000, 1 : 500,000, 1 : 250,000 and 1 : 125,000 of the topographical section of the General Staff, including all maps on these scales of British Africa. A rectilinear approximation to the simple polyconic is also used for the topographical sheets of the Survey of India. The simple polyconic is used for the 1 in. maps of the Militia Department of Canada.
Zenithal Projection by Balance of Errors (Airy’s).—The 10-mile to 1 in. Ordnance map of England.
Projection by Rectangular Spheroidal Co-ordinates.—The 1 : 2500 and the 6 in. Ordnance sheets of the United Kingdom, and the 1 in., 12 in. and 14 in. Ordnance maps of England. The cadastral plans of the Survey of India, and cadastral plans throughout the empire.
Authorities.—See Traité des projections des cartes géographiques, by A. Germain (Paris, 1865) and A Treatise on Projections, by T. Craig, United States Coast and Geodetic Survey (Washington, 1882). Both Germain and Craig (following Germain) make use of the term projections by development, a term which is apt to convey the impression that the spherical surface is developable. As this is not the case, and since such projections are conical, it is best to avoid the use of the term. For the history of the subject see d’Avezac, “Coup d’œil historique sur la projection des cartes géographiques,” Société de géographie de Paris (1863).
J. H. Lambert (Beiträge zum Gebrauch der Mathematik, u.s.w. Berlin, 1772) devised the following projections of the above list: 1, 15, 17, and 21; his transverse cylindrical orthomorphic and the transverse cylindrical equal-area have not been described, as they are seldom used. Among other contributors we mention Mercator, Euler, Gauss, C. B. Mollweide (1774–1825), Lagrange, Cassini, R. Bonne (1727–1795), Airy and Colonel A. R. Clarke. (C. F. Cl.; A. R. C.)
- ↑ The ancient Greeks called a map Pinax, The Romans Tabula geographica. Mappa mundi was the medieval Latin for a map of the world which the ancients called Tabula totius orbis descriptionem continens.
- ↑ Close, “The Ideal Topographical Map,” Geog. Journal, vol. xxv. (1905).
- ↑ K. Peucker, Schattenplastik und Farbenplastik (Vienna, 1898); Geograph. Zeitschrift (1902 and 1908).
- ↑ Professor Henrici, Report on Planimeters (64th meeting of the British Association, Oxford, 1894); J. Tennant, “The Planimeter” (Engineering, xlv. 1903).
- ↑ H. Wagner’s Lehrbuch (Hanover, 1908, pp. 241–252) refers to numerous authorities who deal fully with the whole question of measurement.
- ↑ Kienzl of Leoben in 1891 had invented a similar apparatus which he called a Relief Pantograph (Zeitschrift, Vienna Geog. Soc. 1891).
- ↑ M. Fiorini, Erd- und Himmelsgloben, frei bearbeitet von S. Günther, (Leipzig, 1895).
- ↑ Jahrb. des Polytechn. Instituts in Wien, vol. xv.
- ↑ Compare the maps of Europe, Asia, &c., in this work.
- ↑ The great majority of the maps in this work are made by this process.
- ↑ Lepsius, Urkundenbuch, Pl. XXII.
- ↑ These Colchians certainly were not Egyptians. The maps referred to may have been Assyrian.
- ↑ We are indebted to Strabo for nearly all we know about Greek cartographers anterior to Ptolemy, for none of their maps has been preserved.
- ↑ The gnomon was known to the Chinese in the 5th century B.C., and reached the Greeks (Anaximander) through Babylon. Pytheas, as far as known, was the first to utilize it for the determination of a latitude.
- ↑ If, with W. Dörpfeld, we assume an Attic stadium of 200 steps (500 ft.) to be equal to 164 metres, a degree of 700 stad. would be equal to 114,800 metres, its actual length according to modern measurement being 110,808 metres.
- ↑ Climata based on the length of the longest day were introduced by Hippocrates (c. 400 B.C.). Zones similar to those already drawn out for the celestial sphere were first introduced by the Pythagoreans. Parmenides of Elea (544–430 B.C.) distinguishes five of these zones, viz. a torrid zone, between the tropics of summer and winter, which was uninhabitable on account of heat; two frigid zones, uninhabitable on account of cold, and two intermediate temperate zones.
- ↑ Celestial globes were made much earlier than terrestrial ones. In the museum of Naples there is a celestial globe, 2 metres in diameter, supported upon the shoulders of an Atlas, which E. Heis, judging by the constellations engraved upon it (Atlas coelestis novus, Bonn, 1872) judges to date from the 4th century B.C. It may even be the work of Eudoxus (d. 386 B.C.) the famous astronomer. Aratus of Soli in Cilicia, in his poetical Prognostics of Stars and the World, refers to a globe in his possession. Archimedes, the famous mathematician, had a celestial globe of glass, in the centre of which was a small terrestrial globe. Hero of Alexandria (284–221 B.C.), the ingenious inventor of “Hero’s Fountain,” is believed to have possessed a similar apparatus. The celestial globe of Hipparchus still existed in the Alexandrian library in the time of Ptolemy, who himself refers to globes in his Almagest, as also in the Geography. Leontius, who wrote a book on the manufacture of globes (first published at Basel in 1539), is identified by Fiorini with a bishop of Neapolis (Cyprus) of the time of Constantine III. (642–668).
- ↑ The oldest MS. of Ptolemy's Geography is found in the Vatopedi monastery of Mt Athos. It dates from the 12th or 13th century and was published by Victor Langlois in 1867. For the latest edition we are indebted to the late Carl Müller (Paris, 1883–1906) to whom we are likewise indebted for an edition of the Geographi graeci minores (1855–1861).
- ↑ Facsimiles of it have been published by Desjardins (1869–1871), by K. Miller (1886), who ascribes it to Castorius, a.d. 366, and by others.
- ↑ R. Gough, British Topography (London 1768). His “Histories” are published in Rerum brit. scriptores XL. and LVII. 1866–1869.
- ↑ M. Bittner, Die topogr. Capital des ind. Seespiegels (Vienna, 1897).
- ↑ E. G. Ravenstein, Martin Behaim, his Life and his Globe (London, 1908). On the original only equator, ecliptics, tropics, polar circles and one meridian 80° to the west of Lisbon are laid down.
- ↑ See fig. 23, Catalan Map of the World (1375).
- ↑ J. G. Kohl published facsimiles of the American section of the maps (Weimar, 1860).
- ↑ Facsimiles of the maps of 1507 and 1517 were published by J. Fischer and F. M. von Wieser (Innsbruck, 1903).
- ↑ See “The Survey in British Africa”: the Annual Report of the Colonial Survey Commission.
- ↑ A. Germain, Traité des Projections (Paris, 1865).
- ↑ T. Craig, A Treatise on Projections (U.S. Coast and Geodetic Survey, Washington, 1882).
- ↑ This error is much less than that which may be expected from contraction and expansion of the paper upon which the projection is drawn or printed.