The American Practical Navigator/Chapter 17
CHAPTER 17 - AZIMUTHS AND AMPLITUDES
[edit]INTRODUCTION
[edit]1700. Checking Compass Error
[edit]The navigator must constantly be concerned about the accuracy of the ship’s primary and backup compasses, and should check them regularly. A regularly annotated compass log book will allow the navigator to notice a developing error before it becomes a serious problem.
As long as at least two different types of compass (e.g. mechanical gyro and flux gate, or magnetic and ring laser gyro) are consistent with each other, one can be reasonably sure that there is no appreciable error in either system. Since different types of compasses depend on different scientific principles and are not subject to the same error sources, their agreement indicates almost certainly that no error is present.
A navigational compass can be checked against the heading reference of an inertial navigation system if one is installed. One can also refer to the ship’s indicated GPS track as long as current and leeway are not factors, so that the ship’s COG and heading are in close agreement.
The navigator’s only completely independent directional reference (because it is extra-terrestrial and not man-made) is the sky. The primary compass should be checked occasionally by comparing the observed and calculated azimuths and amplitudes of a celestial body. The difference between the observed and calculated values is the compass error. This chapter discusses these procedures.
Theoretically, these procedures work with any celestial body. However, the Sun and Polaris are used most often when measuring azimuths, and the rising or setting Sun when measuring amplitudes.
While errors can be computed to the nearest tenth of a degree or so, it is seldom possible to steer a ship that accurately, especially when a sea is running, and it is reasonable to round calculations to the nearest half or perhaps whole degree for most purposes.
Various hand-held calculators and computer programs are available to relieve the tedium and errors of tabular and mathematical methods of calculating azimuths and amplitudes. Naval navigators will find the STELLA program useful in this regard. Chapter 20 discusses this program in greater detail.
AZIMUTHS
[edit]1701. Compass Error by Azimuth of the Sun
[edit]Mariners may use Pub 229, Sight Reduction Tables for Marine Navigation to compute the Sun’s azimuth. They compare the computed azimuth to the azimuth measured with the compass to determine compass error. In computing an azimuth, interpolate the tabular azimuth angle for the difference between the table arguments and the actual values of declination, latitude, and local hour angle. Do this triple interpolation of the azimuth angle as follows:
- Enter the Sight Reduction Tables with the nearest integral values of declination, latitude, and local hour angle. For each of these arguments, extract a base azimuth angle.
- Reenter the tables with the same latitude and LHA arguments but with the declination argument 1° greater or less than the base declination argument, depending upon whether the actual declination is greater or less than the base argument. Record the difference between the respondent azimuth angle and the base azimuth angle and label it as the azimuth angle difference (Z Diff.).
- Reenter the tables with the base declination and LHA arguments, but with the latitude argument 1° greater or less than the base latitude argument, depending upon whether the actual (usually DR) latitude is greater or less than the base argument. Record the Z Diff. for the increment of latitude.
- Reenter the tables with the base declination and latitude arguments, but with the LHA argument 1° greater or less than the base LHA argument, depending upon whether the actual LHA is greater or less than the base argument. Record the Z Diff. for the increment of LHA.
- Correct the base azimuth angle for each increment.

Figure 1701. Azimuth by Pub. No. 229.
Example:
In DR latitude 33° 24.0'N, the azimuth of the Sun is 096.5°
pgc. At the time of the observation, the declination of the Sun
is 20° 13.8'N; the local hour angle of the Sun is 316° 41.2'.
Determine compass error.
Solution:
See Figure 1701 Enter the actual value of declination,
DR latitude, and LHA. Round each argument to the nearest
whole degree. In this case, round the declination and the
latitude down to the nearest whole degree. Round the LHA
up to the nearest whole degree. Enter the Sight Reduction
Tables with these whole degree arguments and extract the
base azimuth value for these rounded off arguments.
Record the base azimuth value in the table.
As the first step in the triple interpolation process, increase the value of declination by 1° (to 21°) because the actual declination value was greater than the base declination. Enter the Sight Reduction Tables with the following arguments: (1) Declination = 21°; (2) DR Latitude = 33°; (3) LHA = 317°. Record the tabulated azimuth for these arguments.
As the second step in the triple interpolation process, increase the value of latitude by 1° to 34° because the actual DR latitude was greater than the base latitude. Enter the Sight Reduction Tables with the following arguments: (1) Declination = 20°; (2) DR Latitude = 34°; (3) LHA = 317°. Record the tabulated azimuth for these arguments.
As the third and final step in the triple interpolation process, decrease the value of LHA to 316° because the actual LHA value was smaller than the base LHA. Enter the Sight Reduction Tables with the following arguments: (1) Declination = 20°; (2) DR Latitude = 33°; (3) LHA = 316°. Record the tabulated azimuth for these arguments.
Calculate the Z Difference by subtracting the base azimuth from the tabulated azimuth. Be careful to carry the correct sign.
Z Difference = Tab Z - Base Z
Next, determine the increment for each argument by taking the difference between the actual values of each argument and the base argument. Calculate the correction for each of the three argument interpolations by multiplying the increment by the Z difference and dividing the resulting product by 60.
The sign of each correction is the same as the sign of the corresponding Z difference used to calculate it. In the above example, the total correction sums to −0.1'. Apply this value to the base azimuth of 97.8° to obtain the true azimuth 97.7°. Compare this to the compass reading of 096.5° pgc. The compass error is 1.2°E, which can be rounded to 1° for steering and logging purposes.
AZIMUTH OF POLARIS
[edit]1702. Compass Error By Azimuth Of Polaris
[edit]The Polaris tables in the Nautical Almanac list the azimuth of Polaris for latitudes between the equator and 65° N. Figure 2012 in Chapter 20 shows this table. Compare a compass bearing of Polaris to the tabular value of Polaris to determine compass error. The entering arguments for the table are LHA of Aries and observer latitude.
Example:
On March 17, 2001, at L 33°15.0' N and λ 045°00.0'W,
at 02-00-00 GMT, Polaris bears 358.6° pgc. Calculate the
compass error.
| Date | 17 March 2001 |
| Time (GMT) | 02-00-00 |
| GHA Aries | 204° 43.0' |
| Longitude | 045° 00.0'W |
| LHA Aries | 159° 43.0' |
Solution:
Enter the azimuth section of the Polaris table with the
calculated LHA of Aries. In this case, go to the column for
LHA Aries between 160° and 169°. Follow that column
down and extract the value for the given latitude. Since the
increment between tabulated values is so small, visual
interpolation is sufficient. In this case, the azimuth for
Polaris for the given LHA of Aries and the given latitude
is 359.3°.
| Tabulated Azimuth | 359.2°T |
| Compass Bearing | 358.6°C |
| Error | 0.6°E |
AMPLITUDES
[edit]1703. Amplitudes
[edit]A celestial body’s amplitude angle is the complement of its azimuth angle. At the moment that a body rises or sets, the amplitude angle is the arc of the horizon between the body and the East/West point of the horizon where the observer’s prime vertical intersects the horizon (at 90°), which is also the point where the plane of the equator intersects the horizon (at an angle numerically equal to the observer’s co-latitude). See Figure 1703.
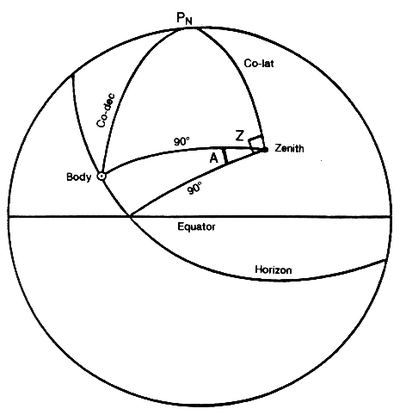
In practical navigation, a bearing (psc or pgc) of a body can be observed when it is on either the celestial or the visible horizon. To determine compass error, simply convert the computed amplitude angle to true degrees and compare it with the observed compass bearing.
The angle is computed by the formula:
sin A = sin Dec / cos Lat.
This formula gives the angle at the instant the body is on the celestial horizon. It does not contain an altitude term because the body’s computed altitude is zero at this instant.
The angle is prefixed E if the body is rising and W if it is setting. This is the only angle in celestial navigation referenced FROM East or West, i.e. from the prime vertical. A body with northerly declination will rise and set North of the prime vertical. Likewise, a body with southerly declination will rise and set South of the prime vertical. Therefore, the angle is suffixed N or S to agree with the name of the body’s declination. A body whose declination is zero rises and sets exactly on the prime vertical.
The Sun is on the celestial horizon when its lower limb is approximately two thirds of a diameter above the visible horizon. The Moon is on the celestial horizon when its upper limb is on the visible horizon. Stars and planets are on the celestial horizon when they are approximately one Sun diameter above the visible horizon.
When observing a body on the visible horizon, a correction from Table 23 must be applied. This correction accounts for the slight change in bearing as the body moves between the visible and celestial horizons. It reduces the bearing on the visible horizon to the celestial horizon, from which the table is computed.
For the Sun, stars, and planets, apply this correction to the observed bearing in the direction away from the elevated pole. For the moon, apply one half of the correction toward the elevated pole. Note that the algebraic sign of the correction does not depend upon the body’s declination, but only on the observer’s latitude. Assuming the body is the Sun the rule for applying the correction can be outlined as follows:
| Observer’s Lat. | Rising/Setting | Observed bearing |
|---|---|---|
| North | Rising | Add to |
| North | Setting | Subtract from |
| South | Rising | Subtract from |
| South | Setting | Add to |
The following two articles demonstrate the procedure for obtaining the amplitude of the Sun on both the celestial and visible horizons.
1704. Amplitude of the Sun on the Celestial Horizon
[edit]Example:
The DR latitude of a ship is 51° 24.6' N. The navigator
observes the setting Sun on the celestial horizon. Its
declination is N 19° 40.4'. Its observed bearing is 303° pgc.
Required:
Gyro error.
Solution:
Interpolate in Table 22 for the Sun’s calculated
amplitude as follows. See Figure 1704. The actual values
for latitude and declination are L = 51.4° N and dec. = N
19.67°. Find the tabulated values of latitude and
declination closest to these actual values. In this case, these
tabulated values are L = 51° and dec. = 19.5°. Record the
amplitude corresponding to these base values, 32.0°, as the
base amplitude.
Next, holding the base declination value constant at 19.5°, increase the value of latitude to the next tabulated value: N 52°. Note that this value of latitude was increased because the actual latitude value was greater than the base value of latitude. Record the tabulated amplitude for L = 52° and dec. = 19.5°: 32.8°. Then, holding the base latitude value constant at 51°, increase the declination value to the next tabulated value: 20°. Record the tabulated amplitude for L = 51° and dec. = 20°: 32.9°.
The latitude’s actual value (51.4°) is 0.4 of the way between the base value (51°) and the value used to determine the tabulated amplitude (52°). The declination’s actual value (19.67°) is 0.3 of the way between the base value (19.5°) and the value used to determine the tabulated amplitude (20.0°). To determine the total correction to base amplitude, multiply these increments (0.4 and 0.3) by the respective difference between the base and tabulated values (+0.8 and +0.9, respectively) and sum the products. The total correction is +0.6°. Add the total correction (+0.6°) to the base amplitude (32.0°) to determine the final amplitude (32.6°) which will be converted to a true bearing.
Because of its northerly declination (in this case), the Sun was 32.6° north of west when it was on the celestial horizon. Therefore its true bearing was 302.6° (270° + 32.6°) at this moment. Comparing this with the gyro bearing of 303° gives an error of 0.4°W, which can be rounded to ½°W.

Figure 1704. Interpolation in Table 22 for Amplitude.
1705. Amplitude of the Sun on the Visible Horizon
[edit]In higher latitudes, amplitude observations should be made when the body is on the visible horizon because the value of the correction is large enough to cause significant error if the observer misjudges the exact position of the celestial horizon. The observation will yield precise results whenever the visible horizon is clearly defined.
Example:
Observer’s DR latitude is 59°47’N, Sun’s declination
is 5°11.3’S. At sunrise the Sun is observed on the visible
horizon bearing 098.5° pgc.
Required:
Compass error.
Solution:
Given this particular latitude and declination, the
amplitude angle is E100.4°S, so that the Sun’s true bearing
is 100.4° at the moment it is on the celestial horizon, that is,
when its Hc is precisely 0°. Applying the Table 23
correction to the observed bearing using the rules given in
Article 1703, the Sun would have been bearing 099.7° pgc
had the observation been made when the Sun was on the
celestial horizon. Therefore, the gyro error is 0.7°E.
1706. Amplitude by Calculation
[edit]As an alternative to using Table 22 and Table 23, a visible horizon amplitude observation can be solved by the “altitude azimuth” formula, because azimuth and amplitude angles are complimentary, and the co-functions of complimentary angles are equal; i.e., cosine Z = sine A.
sin A = [sin D - (sin L sin H)] / (cos L cos H)
For shipboard observations, the Sun’s (computed) altitude is negative 0.7° when it is on the visible horizon. Using the same entities as in Article 1705, the amplitude angle is computed as follows:
sin A = [sin 5.2°− (sin 59.8° X sin −0.7°)] / (cos 59.8° X cos 0.7°) ,