The American Practical Navigator/Chapter 20

by the United States government

CHAPTER 20 - SIGHT REDUCTION

BASIC PROCEDURES

2000. Computer Sight Reduction

The purely mathematical process of sight reduction is an ideal candidate for computerization, and a number of different hand-held calculators and computer programs have been developed to relieve the tedium of working out sights by tabular or mathematical methods. The civilian navigator can choose from a wide variety of hand-held calculators and computer programs which require only the entry of the DR position, altitude and azimuth of the body, and GMT. It is not even necessary to know the name of the body because the computer can figure out what it must be based on the entered data. Calculators and computers provide more accurate solutions than tabular and mathematical methods because they can be based on actual values rather than theoretical assumptions and do not have inherent rounding errors.

U.S. Naval navigators have access to a program called STELLA (System To Estimate Latitude and Longitude Astronomically; do not confuse with a commercial astronomy program with the same name). STELLA was developed by the Astronomical Applications Department of the U.S. Naval Observatory based on a Navy requirement. The algorithms used in STELLA provide an accuracy of one arc-second on the Earth’s surface, a distance of about 30 meters. While this accuracy is far better than can be obtained using a sextant, it does support possible naval needs for automated navigation systems based on celestial objects. These algorithms take into account the oblateness of the Earth, movement of the vessel during sight-taking, and other factors not fully addressed by traditional methods.

STELLA can perform almanac functions, position updating/ DR estimations, celestial body rise/set/transit calculations, compass error calculations, sight planning, and sight reduction. On-line help and user’s guide are included, and it is a component of the Block III NAVSSI. Because STELLA logs all entered data for future reference, it is authorized to replace the Navy Navigation Workbook. STELLA is now an allowance list requirement for Naval ships, and is available from:

Superintendent
U.S. Naval Observatory
Code: AA/STELLA
3450 Massachusetts Ave. NW
Washington, DC, 20392-5420

or on the Navigator of the Navy Web site at

http://www.navigator.navy.mil/navigator/surface.html.

2001. Tabular Sight Reduction

The remainder of this chapter concentrates on sight reduction using the Nautical Almanac and Pub. No. 229, Sight Reduction Tables for Marine Navigation. The method explained here is only one of many methods of reducing a sight. The Nautical Almanac contains directions for solving sights using its own concise sight reduction tables or calculators, along with examples for the current year.

Reducing a celestial sight to obtain a line of position using the tables consists of six steps:

1. Correct the sextant altitude (h_s) to obtain observed altitude (h_o).
2. Determine the body’s GHA and declination (dec.).
3. Select an assumed position (AP) and find its local hour angle (LHA).
4. Compute altitude and azimuth for the AP.
5. Compare the computed and observed altitudes.
6. Plot the line of position.

The introduction to each volume of Pub. 229 contains information: (1) discussing use of the publication for a variety of special celestial navigation techniques; (2) discussing interpolation, explaining the double second difference interpolation required in some sight reductions, and providing tables to facilitate the interpolation process; and (3) discussing the publication’s use in solving problems of great circle sailings. Prior to using Pub. 229, carefully read this introductory material.

Celestial navigation involves determining a circular line of position based on an observer’s distance from a celestial body’s geographic position (GP). Should the observer determine both a body’s GP and his distance from the GP, he would have enough information to plot a line of position; he would be somewhere on a circle whose center was the GP and whose radius equaled his distance from that GP. That circle, from all points on which a body’s measured altitude would be equal, is a circle of equal altitude. There is a direct proportionality between a body’s altitude as measured by an observer and the distance of its GP from that observer; the lower the altitude, the farther away the GP. Therefore, when an observer measures a body’s altitude he obtains an indirect measure of the distance between himself and the body’s GP. Sight reduction is the process of converting that indirect measurement into a line of position.

Sight reduction reduces the problem of scale to manageable size. Depending on a body’s altitude, its GP could be thousands of miles from the observer’s position. The size of a chart required to plot this large distance would be impractical. To eliminate this problem, the navigator does not plot this line of position directly. Indeed, he does not plot the GP at all. Rather, he chooses an assumed position (AP) near, but usually not coincident with, his DR position. The navigator chooses the AP’s latitude and longitude to correspond to the entering arguments of LHA and latitude used in Pub. 229. From Pub. 229, the navigator computes what the body’s altitude would have been had it been measured from the AP. This yields the computed altitude (h_c). He then compares this computed value with the observed altitude (h_o) obtained at his actual position. The difference between the computed and observed altitudes is directly proportional to the distance between the circles of equal altitude for the assumed position and the actual position. Pub. 229 also gives the direction from the GP to the AP. Having selected the assumed position, calculated the distance between the circles of equal altitude for that AP and his actual position, and determined the direction from the assumed position to the body’s GP, the navigator has enough information to plot a line of position (LOP).

To plot an LOP, plot the assumed position on either a chart or a plotting sheet. From the Sight Reduction Tables, determine: 1) the altitude of the body for a sight taken at the AP and 2) the direction from the AP to the GP. Then, determine the difference between the body’s calculated altitude at this AP and the body’s measured altitude. This difference represents the difference in radii between the equal altitude circle passing through the AP and the equal altitude circle passing through the actual position. Plot this difference from the AP either towards or away from the GP along the axis between the AP and the GP. Finally, draw the circle of equal altitude representing the circle with the body’s GP at the center and with a radius equal to the distance between the GP and the navigator’s actual position.

One final consideration simplifies the plotting of the equal altitude circle. Recall that the GP is usually thousands of miles away from the navigator’s position. The equal altitude circle’s radius, therefore, can be extremely large. Since this radius is so large, the navigator can approximate the section close to his position with a straight line drawn perpendicular to the line connecting the AP and the GP. This straight line approximation is good only for sights at relatively low altitudes. The higher the altitude, the shorter the distance between the GP and the actual position, and the smaller the circle of equal altitude. The shorter this distance, the greater the inaccuracy introduced by this approximation.

2002. Selection of the Assumed Position (AP)

Use the following arguments when entering Pub. 229 to compute altitude (h_c) and azimuth:

1. Latitude (L)
2. Declination (d or Dec.)
3. Local hour angle (LHA)

Latitude and LHA are functions of the assumed position. Select an AP longitude resulting in a whole degree of LHA and an AP latitude equal to that whole degree of latitude closest to the DR position. Selecting the AP in this manner eliminates interpolation for LHA and latitude in Pub. 229.

2003. Comparison of Computed and Observed Altitudes

The difference between the computed altitude (h_c) and the observed altitude (h_o) is the altitude intercept (a).

The altitude intercept is the difference in the length of the radii of the circles of equal altitude passing through the AP and the observer’s actual position. The position having the greater altitude is on the circle of smaller radius and is closer to the observed body’s GP. In Figure 2004, the AP is shown on the inner circle. Therefore, h_c is greater than h_o.

Express the altitude intercept in nautical miles and label it T or A to indicate whether the line of position is toward or away from the GP, as measured from the AP.

A useful aid in remembering the relation between h_o, h_c, and the altitude intercept is: H_o M_o T_o for H_o More Toward. Another is C-G-A: Computed Greater Away, remembered as Coast Guard Academy. In other words, if h_o is greater than h_c, the line of position intersects a point measured from the AP towards the GP a distance equal to the altitude intercept. Draw the LOP through this intersection point perpendicular to the axis between the AP and GP.

2004. Plotting the Line of Position

Plot the line of position as shown in Figure 2004. Plot the AP first; then plot the azimuth line from the AP toward or away from the GP. Then, measure the altitude intercept along this line. At the point on the azimuth line equal to the intercept distance, draw a line perpendicular to the azimuth line. This perpendicular represents that section of the circle of equal altitude passing through the navigator’s actual position. This is the line of position.

A navigator often takes sights of more than one celestial body when determining a celestial fix. After plotting the lines of position from these several sights, advance the resulting LOP’s along the track to the time of the last sight and label the resulting fix with the time of this last sight.

Figure 2004. The basis for the line of position from a celestial observation.

2005. Sight Reduction Procedures

Just as it is important to understand the theory of sight reduction, it is also important to develop a practical procedure to reduce celestial sights consistently and accurately. Sight reduction involves several consecutive steps, the accuracy of each completely dependent on the accuracy of the steps that went before. Sight reduction tables have, for the most part, reduced the mathematics involved to simple addition and subtraction. However, careless errors will render even the most skillfully measured sights inaccurate. The navigator using tabular or mathematical techniques must work methodically to reduce careless errors.

Naval navigators will most likely use OPNAV 3530, U.S. Navy Navigation Workbook, which contains pre-formatted pages with “strip forms” to guide the navigator through sight reduction. A variety of commercially-produced forms are also available. Pick a form and learn its method thoroughly. With familiarity will come increasing understanding, speed and accuracy.

Figure 2005 represents a functional and complete worksheet designed to ensure a methodical approach to any sight reduction problem. The recommended procedure discussed below is not the only one available; however, the navigator who uses it can be assured that he has considered every correction required to obtain an accurate fix.

SECTION ONE consists of two parts: (1) Correcting sextant altitude to obtain apparent altitude; and (2) Correcting the apparent altitude to obtain the observed altitude.

Body: Enter the name of the body whose altitude you have measured. If using the Sun or the Moon, indicate which limb was measured.

Index Correction: This is determined by the characteristics of the individual sextant used. Chapter 16 discusses determining its magnitude and algebraic sign.

Dip: The dip correction is a function of the height of eye of the observer. It is always negative; its magnitude is determined from the Dip Table on the inside front cover of the Nautical Almanac.

Sum: Enter the algebraic sum of the dip correction and the index correction.

Sextant Altitude: Enter the altitude of the body measured by the sextant.

Apparent Altitude: Apply the correction determined above to the measured altitude and enter the result as the apparent altitude.

Altitude Correction: Every observation requires an altitude correction. This correction is a function of the apparent altitude of the body. The Almanac contains tables for determining these corrections. For the Sun, planets, and stars, these tables are located on the inside front cover and facing page. For the Moon, these tables are located on the back inside cover and preceding page.

Mars or Venus Additional Correction: As the name implies, this correction is applied to sights of Mars and Venus. The correction is a function of the planet measured, the time of year, and the apparent altitude. The inside front cover of the Almanac lists these corrections.

Additional Correction: Enter this additional correction from Table A-4 located at the front of the Nautical Almanac when obtaining a sight under non-standard atmospheric temperature and pressure conditions. This correction is a function of atmospheric pressure, temperature, and apparent altitude.

Horizontal Parallax Correction: This correction is unique to reducing Moon sights. Obtain the H.P. correction value from the daily pages of the Almanac. Enter the H.P correction table at the back of the Almanac with this value. The H.P correction is a function of the limb of the Moon used (upper or lower), the apparent altitude, and the H.P. correction factor. The H.P. correction is always added to the apparent altitude.

Moon Upper Limb Correction: Enter -30' for this correction if the sight was of the upper limb of the Moon.

Correction to Apparent Altitude: Sum the altitude correction, the Mars or Venus additional correction, the additional correction, the horizontal parallax correction, and the Moon’s upper limb correction. Be careful to determine and carry the algebraic sign of the corrections and their sum correctly. Enter this sum as the correction to the apparent altitude.

Observed Altitude: Apply the Correction to Apparent Altitude algebraically to the apparent altitude. The result is the observed altitude.

SECTION ONE: OBSERVED ALTITUDE
Body	_________________	_________________
Index Correction	_________________	_________________
Dip (height of eye)	_________________	_________________
Sum	_________________	_________________
Sextant Altitude (hs)	_________________	_________________
Apparent Altitude (ha)	_________________	_________________
Altitude Correction	_________________	_________________
Mars or Venus Additional Correction	_________________	_________________
Additional Correction	_________________	_________________
Horizontal Parallax Correction	_________________	_________________
Moon Upper Limb Correction	_________________	_________________
Correction to Apparent Altitude (ha)	_________________	_________________
Observed Altitude (ho)	_________________	_________________
SECTION TWO: GMT TIME AND DATE
Date	_________________	_________________
DR Latitude	_________________	_________________
DR Longitude	_________________	_________________
Observation Time	_________________	_________________
Watch Error	_________________	_________________
Zone Time	_________________	_________________
Zone Description	_________________	_________________
Greenwich Mean Time	_________________	_________________
Date GMT	_________________	_________________
SECTION THREE: LOCAL HOUR ANGLE AND DECLINATION
Tabulated GHA and v Correction Factor	_________________	_________________
GHA Increment	_________________	_________________
Sidereal Hour Angle (SHA) or v Correction	_________________	_________________
GHA	_________________	_________________
+ or - 360° if needed	_________________	_________________
Assumed Longitude (-W, +E)	_________________	_________________
Local Hour Angle (LHA)	_________________	_________________
Tabulated Declination and d Correction Factor	_________________	_________________
d Correction	_________________	_________________
True Declination	_________________	_________________
Assumed Latitude	_________________	_________________
SECTION FOUR: ALTITUDE INTERCEPT AND AZIMUTH
Declination Increment and d Interpolation Factor	_________________	_________________
Computed Altitude (Tabulated)	_________________	_________________
Double Second Difference Correction	_________________	_________________
Total Correction	_________________	_________________
Computed Altitude (hc)	_________________	_________________
Observed Altitude (ho)	_________________	_________________
Altitude Intercept	_________________	_________________
Azimuth Angle	_________________	_________________
True Azimuth	_________________	_________________

Figure 2005. Complete sight reduction form.

SECTION TWO determines the Greenwich Mean Time (GMT; referred to in the Almanacs as Universal time or UT) and GMT date of the sight.

Date: Enter the local time zone date of the sight.

DR Latitude: Enter the dead reckoning latitude of the vessel.

DR Longitude: Enter the dead reckoning longitude of the vessel.

Observation Time: Enter the local time of the sight as recorded on the ship’s chronometer or other timepiece.

Watch Error: Enter a correction for any known watch error.

Zone Time: Correct the observation time with watch error to determine zone time.

Zone Description: Enter the zone description of the time zone indicated by the DR longitude. If the longitude is west of the Greenwich Meridian, the zone description is positive. Conversely, if the longitude is east of the Greenwich Meridian, the zone description is negative. The zone description represents the correction necessary to convert local time to Greenwich Mean Time.

Greenwich Mean Time: Add to the zone description the zone time to determine Greenwich Mean Time.

Date: Carefully evaluate the time correction applied above and determine if the correction has changed the date. Enter the GMT date.

SECTION THREE determines two of the three arguments required to enter Pub. 229: Local Hour Angle (LHA) and Declination. This section employs the principle that a celestial body’s LHA is the algebraic sum of its Greenwich Hour Angle (GHA) and the observer’s longitude. Therefore, the basic method employed in this section is: (1) Determine the body’s GHA; (2) Determine an assumed longitude; (3) Algebraically combine the two quantities, remembering to subtract a western assumed longitude from GHA and to add an eastern longitude to GHA; and (4) Extract the declination of the body from the appropriate Almanac table, correcting the tabular value if required.

Tabulated GHA and v Correction Factor: For the Sun, the Moon, or a planet, extract the value for the whole hour of GHA corresponding to the sight. For example, if the sight was obtained at 13-50-45 GMT, extract the GHA value for 1300. For a star sight reduction, extract the value of the GHA of Aries (GHA ♈), again using the value corresponding to the whole hour of the time of the sight. For a planet or Moon sight reduction, enter the v correction value. This quantity is not applicable to a Sun or star sight. The v correction for a planet sight is found at the bottom of the column for each particular planet. The v correction factor for the Moon is located directly beside the tabulated hourly GHA values. The v correction factor for the Moon is always positive. If a planet’s v correction factor is listed without sign, it is positive. If listed with a negative sign, the planet’s v correction factor is negative. This v correction factor is not the magnitude of the v correction; it is used later to enter the Increments and Correction table to determine the magnitude of the correction.

GHA Increment: The GHA increment serves as an interpolation factor, correcting for the time that the sight differed from the whole hour. For example, in the sight at 13-50-45 discussed above, this increment correction accounts for the 50 minutes and 45 seconds after the whole hour at which the sight was taken. Obtain this correction value from the Increments and Corrections tables in the Almanac. The entering arguments for these tables are the minutes and seconds after the hour at which the sight was taken and the body sighted. Extract the proper correction from the applicable table and enter the correction.

Sidereal Hour Angle or v Correction: If reducing a star sight, enter the star’s Sidereal Hour Angle (SHA). The SHA is found in the star column of the daily pages of the Almanac. The SHA combined with the GHA of Aries results in the star’s GHA. The SHA entry is applicable only to a star. If reducing a planet or Moon sight, obtain the v correction from the Increments and Corrections Table. The correction is a function of only the v correction factor; its magnitude is the same for both the Moon and the planets.

GHA: A star’s GHA equals the sum of the Tabulated GHA of Aries, the GHA Increment, and the star’s SHA. The Sun’s GHA equals the sum of the Tabulated GHA and the GHA Increment. The GHA of the Moon or a planet equals the sum of the Tabulated GHA, the GHA Increment, and the v correction.

+ or – 360° (if needed): Since the LHA will be determined from subtracting or adding the assumed longitude to the GHA, adjust the GHA by 360° if needed to facilitate the addition or subtraction.

Assumed Longitude: If the vessel is west of the prime meridian, the assumed longitude will be subtracted from the GHA to determine LHA. If the vessel is east of the prime meridian, the assumed longitude will be added to the GHA to determine the LHA. Select the assumed longitude to meet the following two criteria: (1) When added or subtracted (as applicable) to the GHA determined above, a whole degree of LHA will result; and (2) It is the longitude closest to that DR longitude that meets criterion (1).

Local Hour Angle (LHA): Combine the body’s GHA with the assumed longitude as discussed above to determine the body’s LHA.

Tabulated Declination and d Correction factor: (1) Obtain the tabulated declination for the Sun, the Moon, the stars, or the planets from the daily pages of the Almanac. The declination values for the stars are given for the entire three day period covered by the daily page of the Almanac. The values for the Sun, Moon, and planets are listed in hourly increments. For these bodies, enter the declination value for the whole hour of the sight. For example, if the sight is at 12-58-40, enter the tabulated declination for 1200. (2) There is no d correction factor for a star sight. There are d correction factors for Sun, Moon, and planet sights. Similar to the v correction factor discussed above, the d correction factor does not equal the magnitude of the d correction; it provides the argument to enter the Increments and Corrections tables in the Almanac. The sign of the d correction factor, which determines the sign of the d correction, is determined by the trend of declination values, not the trend of d values. The d correction factor is simply an interpolation factor; therefore, to determine its sign, look at the declination values for the hours that frame the time of the sight. For example, suppose the sight was taken on a certain date at 12-30-00. Compare the declination value for 1200 and 1300 and determine if the declination has increased or decreased. If it has increased, the d correction factor is positive. If it has decreased, the d correction factor is negative.

d correction: Enter the Increments and Corrections table with the d correction factor discussed above. Extract the proper correction, being careful to retain the proper sign.

True Declination: Combine the tabulated declination and the d correction to obtain the true declination.

Assumed Latitude: Choose as the assumed latitude that whole value of latitude closest to the vessel’s DR latitude. If the assumed latitude and declination are both north or both south, label the assumed latitude “Same.” If one is north and the other is south, label the assumed latitude “Contrary.”

SECTION FOUR uses the arguments of assumed latitude, LHA, and declination determined in Section Three to enter Pub. 229 to determine azimuth and computed altitude. Then, Section Four compares computed and observed altitudes to calculate the altitude intercept. From this the LOP is plotted.

Declination Increment and d Interpolation Factor: Note that two of the three arguments used to enter Pub. 229, LHA and latitude, are whole degree values. Section Three does not determine the third argument, declination, as a whole degree. Therefore, the navigator must interpolate in Pub. 229 for declination, given whole degrees of LHA and latitude. The first steps of Section Four involve this interpolation for declination. Since declination values are tabulated every whole degree in Pub. 229, the declination increment is the minutes and tenths of the true declination. For example, if the true declination is 13° 15.6', then the declination increment is 15.6'.

Pub. 229 also lists a d Interpolation Factor. This is the magnitude of the difference between the two successive tabulated values for declination that frame the true declination. Therefore, for the hypothetical declination listed above, the tabulated d interpolation factor listed in the table would be the difference between declination values given for 13° and 14°. If the declination increases between these two values, d is positive. If the declination decreases between these two values, d is negative.

Computed Altitude (Tabulated): Enter Pub. 229 with the following arguments: (1) LHA from Section Three; (2) assumed latitude from Section Three; (3) the whole degree value of the true declination. For example, if the true declination were 13° 15.6', then enter Pub. 229 with 13° as the value for declination. Record the tabulated computed altitude.

Double Second Difference Correction: Use this correction when linear interpolation of declination for computed altitude is not sufficiently accurate due to the nonlinear change in the computed altitude as a function of declination. The need for double second difference interpolation is indicated by the d interpolation factor appearing in italic type followed by a small dot. When this procedure must be employed, refer to detailed instructions in the introduction to Pub. 229.

Total Correction: The total correction is the sum of the double second difference (if required) and the interpolation corrections. Calculate the interpolation correction by dividing the declination increment by 60' and multiply the resulting quotient by the d interpolation factor.

Computed Altitude (h_c): Apply the total correction, being careful to carry the correct sign, to the tabulated computed altitude. This yields the computed altitude.

Observed Altitude (h_o): Enter the observed altitude from Section One.

Altitude Intercept: Compare h_c and h_o. Subtract the smaller from the larger. The resulting difference is the magnitude of the altitude intercept. If h_o is greater than h_c, then label the altitude intercept “Toward.” If h_c is greater than h_o, then label the altitude intercept “Away.”

Azimuth Angle: Obtain the azimuth angle (Z) from Pub. 229, using the same arguments which determined tabulated computed altitude. Visual interpolation is sufficiently accurate.

True Azimuth: Calculate the true azimuth (Z_n) from the azimuth angle (Z) as follows:

a) If in northern latitudes:
LHA > 180°, then Z_n = Z
LHA < 180°, then Z_n = 360° - Z

b) If in southern latitudes:
LHA > 180°, then Z_n = 180° - Z
LHA < 180°, then Z_n = 180° + Z

SIGHT REDUCTION

The section above discussed the basic theory of sight reduction and presented a method to be followed when reducing sights. This section puts that method into practice in reducing sights of a star, the Sun, the Moon, and planets.

2006. Reducing Star Sights to a Fix

On May 16, 1995, at the times indicated, the navigator takes and records the following sights:

Star	Sextant Altitude	Zone Time
Kochab	47° 19.1'	20-07-43
Spica	32° 34.8'	20-11-26

Height of eye is 48 feet and index correction (IC) is +2.1'. The DR latitude for both sights is 39° N. The DR longitude for the Spica sight is 157° 10'W. The DR longitude for the Kochab sight is 157° 08.0'W. Determine the intercept and azimuth for both sights. See Figure 2006.

First, convert the sextant altitudes to observed altitudes. Reduce the Spica sight first:

Body	Spica
Index Correction	+2.1'
Dip (height 48 ft)	-6.7'
Sum	-4.6'
Sextant Altitude (hs)	32° 34.8'
Apparent Altitude (ha)	32° 30.2'
Altitude Correction	-1.5'
Additional Correction	0
Horizontal Parallax	0
Correction to ha	-1.5'
Observed Altitude (ho)	32° 28.7'

Determine the sum of the index correction and the dip correction. Go to the inside front cover of the Nautical Almanac to the table entitled “DIP.” This table lists dip corrections as a function of height of eye measured in either feet or meters. In the above problem, the observer’s height of eye is 48 feet. The heights of eye are tabulated in intervals, with the correction corresponding to each interval listed between the interval’s endpoints. In this case, 48 feet lies between the tabulated 46.9 to 48.4 feet interval; the corresponding correction for this interval is -6.7'. Add the IC and the dip correction, being careful to carry the correct sign. The sum of the corrections here is -4.6'. Apply this correction to the sextant altitude to obtain the apparent altitude (h_a).

Next, apply the altitude correction. Find the altitude correction table on the inside front cover of the Nautical Almanac next to the dip table. The altitude correction varies as a function of both the type of body sighted (Sun, star, or planet) and the body’s apparent altitude. For the problem above, enter the star altitude correction table. Again, the correction is given within an altitude interval; h_a in this case was 32° 30.2'. This value lies between the tabulated endpoints 32° 00.0' and 33° 45.0'. The correction corresponding to this interval is -1.5'. Applying this correction to ha yields an observed altitude of 32° 28.7'.

Having calculated the observed altitude, determine the time and date of the sight in Greenwich Mean Time:

Date	16 May 1995
DR Latitude	39° N
DR Longitude	157° 10' W
Observation Time	20-11-26
Watch Error	0
Zone Time	20-11-26
Zone Description	+10
GMT	06-11-26
GMT Date	17 May 1995

Record the observation time and then apply any watch error to determine zone time. Then, use the DR longitude at the time of the sight to determine time zone description. In this case, the DR longitude indicates a zone description of +10 hours. Add the zone description to the zone time to obtain GMT. It is important to carry the correct date when applying this correction. In this case, the +10 correction made it 06-11-26 GMT on May 17, when the date in the local time zone was May 16.

After calculating both the observed altitude and the GMT time, enter the daily pages of the Nautical Almanac to calculate the star’s Greenwich Hour Angle (GHA) and declination.

Tab GHA ♈	324° 28.4'
GHA Increment	2° 52.0'
SHA	158° 45.3'
GHA	486° 05.7'
+/- 360°	not required
Assumed Longitude	157° 05.7'
LHA	329°
Tabulated Dec/d	S 11° 08.4'/n.a.
d Correction	—
True Declination	S 11° 08.4'
Assumed Latitude	N 39° contrary

First, record the GHA of Aries from the May 17, 1995 daily page: 324° 28.4'.

Next, determine the incremental addition for the minutes and seconds after 0600 from the Increments and Corrections table in the back of the Nautical Almanac. The increment for 11 minutes and 26 seconds is 2° 52'.

Then, calculate the GHA of the star. Remember:

GHA (star) = GHA ♈ + SHA (star)

The Nautical Almanac lists the SHA of selected stars on each daily page. The SHA of Spica on May17, 1995: 158° 45.3'.

Pub. 229’s entering arguments are whole degrees of LHA and assumed latitude. Remember that LHA = GHA - west longitude or GHA + east longitude. Since in this example the vessel is in west longitude, subtract its assumed longitude from the GHA of the body to obtain the LHA. Assume a longitude meeting the criteria listed in Article 2005.

From those criteria, the assumed longitude must end in 05.7 minutes so that, when subtracted from the calculated GHA, a whole degree of LHA will result. Since the DR longitude was 157° 10.0', then the assumed longitude ending in 05.7' closest to the DR longitude is 157° 05.7'. Subtracting this assumed longitude from the calculated GHA of the star yields an LHA of 329°.

The next value of concern is the star’s true declination. This value is found on the May 17th daily page next to the star’s SHA. Spica’s declination is S 11° 08.4'. There is no d correction for a star sight, so the star’s true declination equals its tabulated declination. The assumed latitude is determined from the whole degree of latitude closest to the DR latitude at the time of the sight. In this case, the assumed latitude is N 39°. It is marked “contrary” because the DR latitude is north while the star’s declination is south.

The following information is known: (1) the assumed position’s LHA (329°) and assumed latitude (39°N contrary name); and (2) the body’s declination (S11° 08.4').

Find the page in the Sight Reduction Table corresponding to an LHA of 329° and an assumed latitude of N 39°, with latitude contrary to declination. Enter this table with the body’s whole degree of declination. In this case, the body’s whole degree of declination is 11°. This declination corresponds to a tabulated altitude of 32° 15.9'. This value is for a declination of 11°; the true declination is 11° 08.4'. Therefore, interpolate to determine the correction to add to the tabulated altitude to obtain the computed altitude.

The difference between the tabulated altitudes for 11° and 12° is given in Pub. 229 as the value d; in this case, d = -53.0. Express as a ratio the declination increment (in this case, 8.4') and the total interval between the tabulated declination values (in this case, 60') to obtain the percentage of the distance between the tabulated declination values represented by the declination increment. Next, multiply that percentage by the increment between the two values for computed altitude. In this case:

${\frac {8.4}{60}}\times (-53.0)=-7.4$

Subtract 7.4' from the tabulated altitude to obtain the final computed altitude: H_c = 32° 08.5'.

Dec Inc / + or − d	8.4' / -53.0
hc (tabulated)	32° 15.9'
Correction (+ or −)	−7.4'
hc (computed)	32° 08.5'

It will be valuable here to review exactly what h_o and h_c represent. Recall the methodology of the altitude-intercept method. The navigator first measures and corrects an altitude for a celestial body. This corrected altitude, h_o, corresponds to a circle of equal altitude passing through the navigator’s actual position whose center is the geographic position (GP) of the body. The navigator then determines an assumed position (AP) near, but not coincident with, his actual position; he then calculates an altitude for an observer at that assumed position (AP). The circle of equal altitude passing through this assumed position is concentric with the circle of equal altitude passing through the navigator’s actual position. The difference between the body’s altitude at the assumed position (h_c) and the body’s observed altitude (h_o) is equal to the differences in radii length of the two corresponding circles of equal altitude. In the above problem, therefore, the navigator knows that the equal altitude circle passing through his actual position is:

h_o = 32°28.7'     

−h_c = 32°08.5'     

20.2 NM

away from the equal altitude circle passing through his assumed position. Since h_o is greater than h_c, the navigator knows that the radius of the equal altitude circle passing through his actual position is less than the radius of the equal altitude circle passing through the assumed position.

The only remaining question is: in what direction from the assumed position is the body’s actual GP. Pub. 229 also provides this final piece of information. This is the value for Z tabulated with the h_c and d values discussed above. In this case, enter Pub. 229 as before, with LHA, assumed latitude, and declination. Visual interpolation is sufficient. Extract the value Z = 143.3°. The relation between Z and Zn, the true azimuth, is as follows:

In northern latitudes:

LHA > 180°, then Z_n = Z

LHA < 180°, then Z_n = 360°–Z

In southern latitudes:

LHA > 180°, then Z_n = 180° – Z

LHA < 180°, then Z_n = 180°+Z

In this case, LHA > 180° and the vessel is in northern latitude. Therefore, Z_n = Z = 143.3°T. The navigator now has enough information to plot a line of position.

The values for the reduction of the Kochab sight follow:

Body	Kochab
Index Correction	+2.1'
Dip Correction	−6.7'
Sum	−4.6'
hs	47° 19.1'
ha	47° 14.5'
Altitude Correction	−.9'
Additional Correction	not applicable
Horizontal Parallax	not applicable
Correction to ha	−9'
ho	47° 13.6'
Date	16 May 1995
DR latitude	39°N
DR longitude 157°	08.0' W
Observation Time	20-07-43
Watch Error	0
Zone Time	20-07-43
Zone Description	+10
GMT	06-07-43
T Date	17 May 1995
Tab GHA ♈	324° 28.4'
GHA Increment	1° 56.1'
SHA	137° 18.5'
GHA	463° 43.0'
+/- 360°	not applicable
Assumed Longitude	156° 43.0'
LHA	307°
Tab Dec / d	N74° 10.6' / n.a.
d Correction	not applicable
True Declination	N74° 10.6'
Assumed Latitude	39°N (same)
Dec Inc / + or - d	10.6' / −24.8
hc	47° 12.6'
Total Correction	−4.2'
hc (computed)	47° 08.4'
ho	47° 13.6'
a (intercept)	5.2 towards
Z	018.9°
Zn	018.9°

Figure 2006. Left hand daily page of the Nautical Almanac for May 17, 1995.

2007. Reducing a Sun Sight

The example below points out the similarities between reducing a Sun sight and reducing a star sight. It also demonstrates the additional corrections required for low altitude (<10°) sights and sights taken during non-standard temperature and pressure conditions.

On June 16, 1994, at 05-15-23 local time, at DR position L 30°N λ 45°W, a navigator takes a sight of the Sun’s upper limb. The navigator has a height of eye of 18 feet, the temperature is 88° F, and the atmospheric pressure is 982 mb. The sextant altitude is 3° 20.2'. There is no index error. Determine the observed altitude. See Figure 2007.

Apply the index and dip corrections to h_s to obtain h_a. Because h_a is less than 10°, use the special altitude correction table for sights between 0° and 10° located on the right inside front page of the Nautical Almanac.

Enter the table with the apparent altitude, the limb of the Sun used for the sight, and the period of the year. Interpolation for the apparent altitude is not required. In this case, the table yields a correction of −29.4'. The correction’s algebraic sign is found at the head of each group of entries and at every change of sign.

The additional correction is required because of the non-standard temperature and atmospheric pressure under which the sight was taken. The correction for these nonstandard conditions is found in the Additional Corrections table located on page A4 in the front of the Nautical Almanac.

First, enter the Additional Corrections table with the temperature and pressure to determine the correct zone letter: in this case, zone L. Then, locate the correction in the L column corresponding to the apparent altitude of 3° 16.1'. Interpolate between the table arguments of 3° 00.0' and 3° 30.0' to determine the additional correction: +1.4'. The total correction to the apparent altitude is the sum of the altitude and additional corrections: −28.0'. This results in an h_o of 2° 48.1'.

Next, determine the Sun’s GHA and declination.

Body	Sun UL
Index Correction	0
Dip Correction (18 ft)	−4.1'
Sum	−4.1'
hs	3° 20.2'
ha	3° 16.1'
Altitude Correction	−29.4'
Additional Correction	+1.4'
Horizontal Parallax	0
Correction to ha	−28.0'
ho	2° 48.1'
Date	June 16, 1994
DR Latitude	N30° 00.0'
DR Longitude	W045° 00.0'
Observation Time	05-15-23
Watch Error	0
Zone Time	05-15-23
Zone Description	+03
GMT	08-15-23
Date GMT	June 16, 1994
Tab GHA / v	299° 51.3' / n.a.
GHA Increment	3° 50.8'
SHA or v correction	not applicable
GHA	303°42.1'
Assumed Longitude	44° 42.1' W
LHA	259°
Tab Declination / d	N23° 20.5' / +0.1'
d Correction	0.0
True Declination	N23° 20.5'
Assumed Latitude	N30° (same)

Again, this process is similar to the star sights reduced above. Notice, however, that SHA, a quantity unique to star sight reduction, is not used in Sun sight reduction.

Determining the Sun’s GHA is less complicated than determining a star’s GHA. The Nautical Almanac’s daily pages list the Sun’s GHA in hourly increments. In this case, the Sun’s GHA at 0800 GMT on June 16, 1994 is 299° 51.3'. The v correction is not applicable for a Sun sight; therefore, applying the increment correction yields the Sun’s GHA. In this case, the GHA is 303° 42.1'.

Determining the Sun’s LHA is similar to determining a star’s LHA. In determining the Sun’s declination, however, an additional correction not encountered in the star sight, the d correction, must be considered. The bottom of the Sun column on the daily pages of the Nautical Almanac lists the d value. This is an interpolation factor for the Sun’s declination. The sign of the d factor is not given; it must be determined by noting from the Almanac if the Sun’s declination is increasing or decreasing throughout the day. If it is increasing, the factor is positive; if it is decreasing, the factor is negative. In the above problem, the Sun’s declination is increasing throughout the day. Therefore, the d factor is +0.1.

Having obtained the d factor, enter the 15 minute increment and correction table. Under the column labeled “v or d corrⁿ,” find the value for d in the left hand column. The corresponding number in the right hand column is the correction; apply it to the tabulated declination. In this case, the correction corresponding to a d value of +0.1 is 0.0'.

Correction (+ or −)	+10.8'
Computed Altitude (hc)	2° 39.6'
Observed Altitude (ho)	2° 48.1'
Intercept	8.5 NM (towards)
Z	064.7°
Zn	064.7°

The final step will be to determine h_c and Z_n. Enter Pub. 229 with an LHA of 259°, a declination of N23° 20.5', and an assumed latitude of 30°N.

Declination Increment / + or − d	20.5' / +31.5
Tabulated Altitude	2° 28.8'

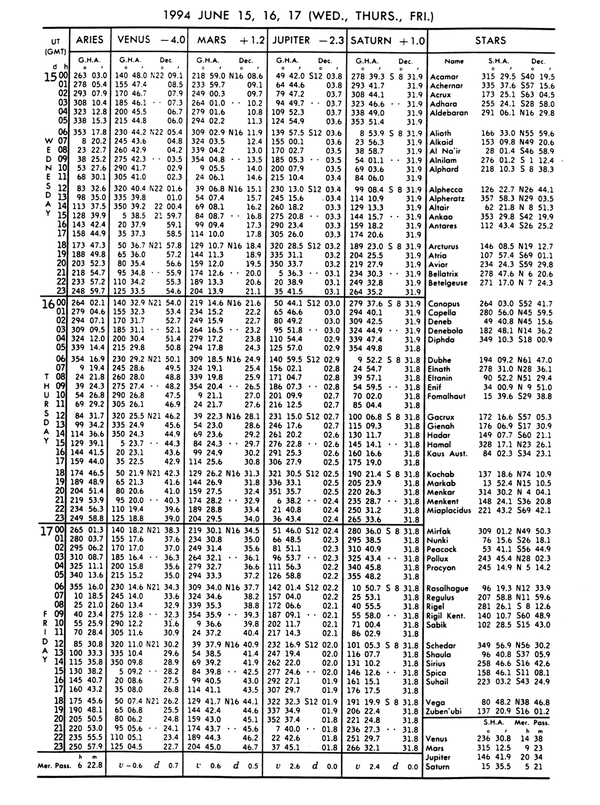
Figure 2007. Left hand daily page of the Nautical Almanac for June 16, 1994.

2008. Reducing a Moon Sight

The Moon is easy to identify and is often visible during the day. However, the Moon’s proximity to the Earth requires applying additional corrections to h_a to obtain h_o. This article will cover Moon sight reduction.

At 10-00-00 GMT, June 16, 1994, the navigator obtains a sight of the Moon’s upper limb. H_s is 26° 06.7'. Height of eye is 18 feet; there is no index error. Determine h_o, the Moon’s GHA, and the Moon’s declination. See Figure 2008.

This example demonstrates the extra corrections required for obtaining h_o for a Moon sight. Apply the index and dip corrections in the same manner as for star and Sun sights. The altitude correction comes from tables located on the inside back covers of the Nautical Almanac.

In this case, the apparent altitude was 26° 02.6'. Enter the altitude correction table for the Moon with the above apparent altitude. Interpolation is not required. The correction is +60.5'. The additional correction in this case is not applicable because the sight was taken under standard temperature and pressure conditions.

The horizontal parallax correction is unique to Moon sights. The table for determining this HP correction is on the back inside cover of the Nautical Almanac. First, go to the daily page for June 16 at 10-00-00 GMT. In the column for the Moon, find the HP correction factor corresponding to 10-00-00. Its value is 58.4. Take this value to the HP correction table on the inside back cover of the Almanac. Notice that the HP correction columns line up vertically with the Moon altitude correction table columns. Find the HP correction column directly under the altitude correction table heading corresponding to the apparent altitude. Enter that column with the HP correction factor from the daily pages. The column has two sets of figures listed under “U” and “L” for upper and lower limb, respectively. In this case, trace down the “U” column until it intersects with the HP correction factor of 58.4. Interpolating between 58.2 and 58.5 yields a value of +4.0' for the horizontal parallax correction.

Body	Moon (UL)
Index Correction	0.0'
Dip (18 feet)	−4.1'
Sum	−4.1'
Sextant Altitude (hs)	26° 06.7'
Apparent Altitude (ha)	26° 02.6'
Altitude Correction	+60.5'
Additional Correction	0.0'
Horizontal Parallax (58.4)	+4.0'
Moon Upper Limb Correction	−30.0'
Correction to ha	+34.5'
Observed Altitude (ho)	26° 37.1'

The final correction is a constant -30.0' correction to h_a applied only to sights of the Moon’s upper limb. This correction is always negative; apply it only to sights of the Moon’s upper limb, not its lower limb. The total correction to h_a is the sum of all the corrections; in this case, this total correction is +34.5 minutes.

To obtain the Moon’s GHA, enter the daily pages in the Moon column and extract the applicable data just as for a star or Sun sight. Determining the Moon’s GHA requires an additional correction, the v correction.

GHA Moon and v	245° 45.1' and +11.3
GHA Increment	0° 00.0'
v Correction	+0.1'
GHA	245° 45.2'

First, record the GHA of the Moon for 10-00-00 on June 16, 1994, from the daily pages of the Nautical Almanac. Record also the v correction factor; in this case, it is +11.3. The v correction factor for the Moon is always positive. The increment correction is, in this case, zero because the sight was recorded on the even hour. To obtain the v correction, go to the tables of increments and corrections. In the 0 minute table in the v or d correction columns, find the correction that corresponds to a v = 11.3. The table yields a correction of +0.1'. Adding this correction to the tabulated GHA gives the final GHA as 245° 45.2'.

Finding the Moon’s declination is similar to finding the declination for the Sun or stars. Go to the daily pages for June 16, 1994; extract the Moon’s declination and d factor.

Tabulated Declination / d	S 00° 13.7' / +12.1
d Correction	+0.1'
True Declination	S 00° 13.8'

The tabulated declination and the d factor come from the Nautical Almanac’s daily pages. Record the declination and d correction and go to the increment and correction pages to extract the proper correction for the given d factor. In this case, go to the correction page for 0 minutes. The correction corresponding to a d factor of +12.1 is +0.1. It is important to extract the correction with the correct algebraic sign. The d correction may be positive or negative depending on whether the Moon’s declination is increasing or decreasing in the interval covered by the d factor. In this case, the Moon’s declination at 10-00-00 GMT on 16 June was S 00° 13.7'; at 11-00-00 on the same date the Moon’s declination was S 00° 25.8'. Therefore, since the declination was increasing over this period, the d correction is positive. Do not determine the sign of this correction by noting the trend in the d factor. In other words, had the d factor for 11-00-00 been a value less than 12.1, that would not indicate that the d correction should be negative. Remember that the d factor is analogous to an interpolation factor; it provides a correction to declination. Therefore, the trend in declination values, not the trend in d values, controls the sign of the d correction. Combine the tabulated declination and the d correction factor to determine the true declination. In this case, the Moon’s true declination is S 00° 13.8'.

Having obtained the Moon’s GHA and declination, calculate LHA and determine the assumed latitude. Enter the Sight Reduction Table with the LHA, assumed latitude, and calculated declination. Calculate the intercept and azimuth in the same manner used for star and Sun sights.

Figure 2008. Right hand daily page of the Nautical Almanac for June 16, 1994.

2009. Reducing a Planet Sight

There are four navigational planets: Venus, Mars, Jupiter, and Saturn. Reducing a planet sight is similar to reducing a Sun or star sight, but there are a few important differences. This Article will cover the procedure for determining h_o, the GHA and the declination for a planet sight.

On July 27, 1995, at 09-45-20 GMT, you take a sight of Mars. H_s is 33° 20.5'. The height of eye is 25 feet, and the index correction is +0.2'. Determine h_o, GHA, and declination. See Figure 2009.

The table below XX demonstrates the similarity between reducing planet sights and reducing sights of the Sun and stars. Calculate and apply the index and dip corrections exactly as for any other sight. Take the resulting apparent altitude and enter the altitude correction table for the stars and planets on the inside front cover of the Nautical Almanac.

Body	Mars
Index Correction	+0.2'
Dip Correction (25 feet)	−4.9'
Sum	−4.7'
hs	33° 20.5'
ha	33° 15.8'
Altitude Correction	−1.5'
Additional Correction	Not applicable
Horizontal Parallax	Not applicable
Additional Correction for Mars	+0.1'
Correction to ha	−1.4'
ho	33° 14.4'

In this case, the altitude correction for 33° 15.8' results in a correction of -1.5'. The additional correction is not applicable because the sight was taken at standard temperature and pressure; the horizontal parallax correction is not applicable to a planet sight. All that remains is the correction specific to Mars or Venus. The altitude correction table in the Nautical Almanac also contains this correction. Its magnitude is a function of the body sighted (Mars or Venus), the time of year, and the body’s apparent altitude. Entering this table with the data for this problem yields a correction of +0.1'. Applying these corrections to h_a results in an h_o of 33° 14.4'.

Tabulated GHA / v	256°10.6' / 1.1
GHA Increment	11° 20.0'
v correction	+0.8'
GHA	267°31.4'

The only difference between determining the Sun’s GHA and a planet’s GHA lies in applying the v correction. Calculate this correction from the v or d correction section of the Increments and Correction table in the Nautical Almanac. Find the v factor at the bottom of the planets’ GHA columns on the daily pages of the Nautical Almanac. For Mars on July 27, 1995, the v factor is 1.1. If no algebraic sign precedes the v factor, add the resulting correction to the tabulated GHA. Subtract the resulting correction only when a negative sign precedes the v factor. Entering the v or d correction table corresponding to 45 minutes yields a correction of 0.8'. Remember, because no sign preceded the v factor on the daily pages, add this correction to the tabulated GHA. The final GHA is 267°31.4'.

Tabulated Declination / d	S 01° 06.1' / 0.6
d Correction	+0.5'
True Declination	S 01° 06.6'

Read the tabulated declination directly from the daily pages of the Nautical Almanac. The d correction factor is listed at the bottom of the planet column; in this case, the factor is 0.6. Note the trend in the declination values for the planet; if they are increasing during the day, the correction factor is positive. If the planet’s declination is decreasing during the day, the correction factor is negative. Next, enter the v or d correction table corresponding to 45 minutes and extract the correction for a d factor of 0.6. The correction in this case is +0.5'.

From this point, reducing a planet sight is exactly the same as reducing a Sun sight.

Figure 2009. Left hand daily page of the Nautical Almanac for July 27, 1995.

MERIDIAN PASSAGE

This section covers determining both latitude and longitude at the meridian passage of the Sun, or Local Apparent Noon (LAN). Determining a vessel’s latitude at LAN requires calculating the Sun’s zenith distance and declination and combining them according to the rules discussed below.

Latitude at LAN is a special case of the navigational triangle where the Sun is on the observer’s meridian and the triangle becomes a straight north/south line. No “solution” is necessary, except to combine the Sun’s zenith distance and its declination according to the rules discussed below. Longitude at LAN is a function of the time elapsed since the Sun passed the Greenwich meridian. The navigator must determine the time of LAN and calculate the GHA of the Sun at that time. The following examples demonstrates these processes.

2010. Latitude at Meridian Passage

At 1056 ZT, May 16, 1995, a vessel’s DR position is L 40° 04.3'N and λ 157° 18.5' W. The ship is on course 200°T at a speed of ten knots. (1) Calculate the first and second estimates of Local Apparent Noon. (2) The navigator actually observes LAN at 12-23-30 zone time. The sextant altitude at LAN is 69° 16.0'. The index correction is +2.1' and the height of eye is 45 feet. Determine the vessel’s latitude.

First, determine the time of meridian passage from the daily pages of the Nautical Almanac. In this case, the meridian passage for May 16, 1995, is 1156. That is, the Sun crosses the central meridian of the time zone at 1156 ZT and the observer’s local meridian at 1156 local time. Next, determine the vessel’s DR longitude for the time of meridian passage. In this case, the vessel’s 1156 DR longitude is 157° 23.0' W. Determine the time zone in which this DR longitude falls and record the longitude of that time zone’s central meridian. In this case, the central meridian is 150° W. Enter the Conversion of Arc to Time table in the Nautical Almanac with the difference between the DR longitude and the central meridian longitude. The conversion for 7° of arc is 28^m of time, and the conversion for 23' of arc is 1^m32^s of time. Sum these two times. If the DR position is west of the central meridian (as it is in this case), add this time to the time of tabulated meridian passage. If the longitude difference is to the east of the central meridian, subtract this time from the tabulated meridian passage. In this case, the DR position is west of the central meridian. Therefore, add 29 minutes and 32 seconds to 1156, the tabulated time of meridian passage. The estimated time of LAN is 12-25-32 ZT.

This first estimate for LAN does not take into account the vessel’s movement. To calculate the second estimate of LAN, first determine the DR longitude for the time of first estimate of LAN (12-25-32 ZT). In this case, that longitude would be 157° 25.2' W. Then, calculate the difference between the longitude of the 12-25-32 DR position and the central meridian longitude. This would be 7° 25.2'. Again, enter the arc to time conversion table and calculate the time difference corresponding to this longitude difference. The correction for 7° of arc is 28' of time, and the correction for 25.2' of arc is 1'41" of time. Finally, apply this time correction to the original tabulated time of meridian passage (1156 ZT). The resulting time, 12-25-41 ZT, is the second estimate of LAN.

Solving for latitude requires that the navigator calculate two quantities: the Sun’s declination and the Sun’s zenith distance. First, calculate the Sun’s true declination at LAN. The problem states that LAN is 12-28-30. (Determining the exact time of LAN is covered in Article 2011.) Enter the time of observed LAN and add the correct zone description to determine GMT. Determine the Sun’s declination in the same manner as in the sight reduction problem in Article 2006. In this case, the tabulated declination was N 19° 19.1', and the d correction +0.2'. The true declination, therefore, is N 19° 19.3'.

Next, calculate zenith distance. Recall from Navigational Astronomy that zenith distance is simply 90° - observed altitude. Therefore, correct h_s to obtain h_a; then correct h_a to obtain h_o. Then, subtract h_o from 90° to determine the zenith distance. Name the zenith distance North or South depending on the relative position of the observer and the Sun’s declination. If the observer is to the north of the Sun’s declination, name the zenith distance north. Conversely, if the observer is to the south of the Sun’s declination, name the zenith distance south. In this case, the DR latitude is N 39° 55.0' and the Sun’s declination is N 19° 19.3'. The observer is to the north of the Sun’s declination; therefore, name the zenith distance north. Next, compare the names of the zenith distance and the declination. If their names are the same (i.e., both are north or both are south), add the two values together to obtain the latitude. This was the case in this problem. Both the Sun’s declination and zenith distance were north; therefore, the observer’s latitude is the sum of the two.

Date	16 May 1995
DR Latitude (1156 ZT)	39° 55.0' N
DR Longitude (1156 ZT)	157° 23.0' W
Central Meridian	150° W
d Longitude (arc)	7° 23' W
d Longitude (time)	+29 min. 32 sec
Meridian Passage (LMT)	1156
ZT (first estimate)	12-25-32
DR Longitude (12-25-32)	157° 25.2'
d Longitude (arc)	7° 25.2'
d Longitude (time)	+29 min. 41 sec
Meridian Passage	1156
ZT (second estimate)	12-25-41
ZT (actual transit)	12-23-30 local
Zone Description	+10
GMT	22-23-30
Date (GMT)	16 May 1995
Tabulated Declination / d	N 19° 09.0' / +0.6
d correction	+0.2'
True Declination	N 19° 09.2'
Index Correction	+2.1'
Dip (48 ft)	-6.7'
Sum	-4.6'
hs (at LAN)	69° 16.0'
ha 69°	11.4'
Altitude Correction	+15.6'
89° 60'	89° 60.0'
ho 69°	27.0'
Zenith Distance	N 20° 33.0'
True Declination	N 19° 09.2'
Latitude	39° 42.2'

If the name of the body’s zenith distance is contrary to the name of the Sun’s declination, then subtract the smaller of the two quantities from the larger, carrying for the name of the difference the name of the larger of the two quantities. The result is the observer’s latitude. The following examples illustrate this process.

Zenith Distance	N 25°
True Declination	S 15°
Latitude	N 10°
Zenith Distance	S 50°
True Declination	N 10°
Latitude	S 40°

2011. Longitude at Meridian Passage

Determining a vessel’s longitude at LAN is straightforward. In the western hemisphere, the Sun’s GHA at LAN equals the vessel’s longitude. In the eastern hemisphere, subtract the Sun’s GHA from 360° to determine longitude. The difficult part lies in determining the precise moment of meridian passage.

Determining the time of meridian passage presents a problem because the Sun appears to hang for a finite time at its local maximum altitude. Therefore, noting the time of maximum sextant altitude is not sufficient for determining the precise time of LAN. Two methods are available to obtain LAN with a precision sufficient for determining longitude: (1) the graphical method and (2) the calculation method. The graphical method is discussed first below.

See Figure 2011. For about 30 minutes before the estimated time of LAN, measure and record several sextant altitudes and their corresponding times. Continue taking sights for about 30 minutes after the Sun has descended from the maximum recorded altitude. Increase the sighting frequency near the meridian passage. One sight every 20-30 seconds should yield good results near meridian passage; less frequent sights are required before and after. Plot the resulting data on a graph of sextant altitude versus time and draw a fair curve through the plotted data. Next, draw a series of horizontal lines across the curve formed by the data points. These lines will intersect the faired curve at two different points. The x coordinates of the points where these lines intersect the faired curve represent the two different times when the Sun’s altitude was equal (one time when the Sun was ascending; the other time when the Sun was descending). Draw three such lines, and ensure the lines have sufficient vertical separation. For each line, average the two times where it intersects the faired curve. Finally, average the three resulting times to obtain a final value

for the time of LAN. From the Nautical Almanac, determine the Sun’s GHA at that time; this is your longitude in the western hemisphere. In the eastern hemisphere, subtract the Sun’s GHA from 360° to determine longitude. For a quicker but less exact time, simply drop a perpendicular from the apex of the curve and read the time along the time scale. The second method of determining LAN is similar to the first. Estimate the time of LAN as discussed above, Measure and record the Sun’s altitude as the Sun approaches its maximum altitude. As the Sun begins to descend, set the sextant to correspond to the altitude recorded just before the Sun’s reaching its maximum altitude. Note the time when the Sun is again at that altitude. Average the two times. Repeat this procedure with two other altitudes recorded before LAN, each time presetting the sextant to those altitudes and recording the corresponding times that the Sun, now on its descent, passes through those altitudes. Average these corresponding times. Take a final average among the three averaged times; the result will be the time of meridian passage. Determine the vessel’s longitude by determining the Sun’s GHA at the exact time of LAN.

Figure 2011. Time of LAN.

LATITUDE BY POLARIS

2012. Latitude by Polaris

Since Polaris is always within about 1° of the North Pole, the altitude of Polaris, with a few minor corrections, equals the latitude of the observer. This relationship makes Polaris an extremely important navigational star in the northern hemisphere.

The corrections are necessary because Polaris orbits in a small circle around the pole. When Polaris is at the exact same altitude as the pole, the correction is zero. At two points in its orbit it is in a direct line with the observer and the pole, either nearer than or beyond the pole. At these points the corrections are maximum. The following example illustrates converting a Polaris sight to latitude.

At 23-18-56 GMT, on April 21, 1994, at DR Lat. 50° 23.8' N, λ=37° 14.0' W, the observed altitude of Polaris (h_o) is 49° 31.6'. Find the vessel’s latitude.

To solve this problem, use the equation:

Latitude = h_o – 1° + A0 + A1 + A2

where h_o is the sextant altitude (h_s) corrected as in any other star sight; 1° is a constant; and A0, A1, and A2 are correction factors from the Polaris tables found in the Nautical Almanac. These three correction factors are always positive. One needs the following information to enter the tables: LHA of Aries, DR latitude, and the month of the year. Therefore:

Enter the Polaris table with the calculated LHA of Aries (162° 03.5'). See Figure 2012. The first correction, A0, is a function solely of the LHA of Aries. Enter the table column indicating the proper range of LHA of Aries; in this case, enter the 160°-169° column. The numbers on the left hand side of the A0 correction table represent the whole degrees of LHA ♈; interpolate to determine the proper A0 correction. In this case, LHA ♈ was 162° 03.5'. The A0 correction for LHA = 162° is 1° 25.4' and the A0 correction for LHA = 163° is 1° 26.1'. The A0 correction for 162° 03.5' is 1° 25.4'.

To calculate the A1 correction, enter the A1 correction table with the DR latitude, being careful to stay in the 160°- 169° LHA column. There is no need to interpolate here; simply choose the latitude that is closest to the vessel’s DR latitude. In this case, L is 50°N. The A1 correction corresponding to an LHA range of 160°-169° and a latitude of 50°N is + 0.6'.

Finally, to calculate the A2 correction factor, stay in the 160°-169° LHA column and enter the A2 correction table. Follow the column down to the month of the year; in this case, it is April. The correction for April is + 0.9'.

Sum the corrections, remembering that all three are always positive. Subtract 1° from the sum to determine the total correction; then apply the resulting value to the observed altitude of Polaris. This is the vessel’s latitude.

Tabulated GHA ♈ (2300 hrs.)	194° 32.7'
Increment (18-56)	4° 44.8'
GHA ♈	199° 17.5'
DR Longitude (-W +E)	37° 14.0'
LHA ♈	162° 03.5'
A0 (162° 03.5')	+1° 25.4'
A1 (L = 50°N)	+0.6'
A2 (April)	+0.9'
Sum	1° 26.9'
Constant	−1° 00.0'
Observed Altitude	49° 31.6'
Total Correction	+26.9'
Latitude	N 49° 58.5'

Figure 2012. Excerpt from the Polaris Tables.

THE DAY’S WORK IN CELESTIAL NAVIGATION

2013. Celestial Navigation Daily Routine

The navigator need not follow the entire celestial routine if celestial navigation is not the primary navigation method. It is appropriate to use only the steps of the celestial day’s work that are necessary to provide a meaningful check on the primary fix source and maintain competency in celestial techniques.

The list of procedures below provides a complete daily celestial routine to follow. This sequence works equally well for all sight reduction methods, whether tabular, mathematical, computer program, or celestial navigation calculator. See Figure 2013 for an example of a typical day’s celestial plot.

1. Before dawn, compute the time of morning twilight and plot the dead reckoning position for that time.

2. At morning twilight, take and reduce celestial observations for a fix. At sunrise take an amplitude of the Sun for a compass check.

3. Mid-morning, wind the chronometer and determine chronometer error with a radio time tick.

4. Mid-morning, reduce a Sun sight for a morning Sun line.

5. Calculate an azimuth of the Sun for a compass check, if no amplitude was taken at sunrise.

6. At LAN, obtain a Sun line and advance the morning Sun line for the noon fix. Compute a longitude determined at LAN for an additional LOP.

7. Mid afternoon, again take and reduce a Sun sight. This is primarily for use with an advanced noon Sun line, or with a Moon or Venus line if the skies are overcast during evening twilight.

8. Calculate an azimuth of the Sun for a compass check at about the same time as the afternoon Sun observation. The navigator may replace this azimuth with an amplitude observation at sunset.

9. During evening twilight, reduce celestial observations for a fix.

10. Be alert at all times for the moon or brighter planets which may be visible during daylight hours for additional LOP’s, and Polaris at twilight for a latitude line.

Chapter 7, Chapter 17, and Chapter 20 contain detailed explanations of the procedures required to carry out the various functions of this routine.

Figure 2013. Typical celestial plot at sea.