Translation:On the Non-Euclidean Interpretation of the Theory of Relativity
On the Non-Euclidean Interpretation of the Theory of Relativity
Lecture held at the Jahresversammlung der Deutschen Mathematiker-Vereinigung zu Karlsruhe.
By Vladimir Varićak in Agram.
That a similar process occurred by formulating the theory of relativity, as in geometry when the non-euclidean – specifically the Lobachevsky-Boljai – geometry came into light, was presumably anticipated by some. It is namely very remarkable that some authors mention the non-euclidean geometry when they interpret relativity theory, without ascribing any value to it for the description of natural phenomena. Some almost deny that it has any value in this respect, like Lewis who considers the non-euclidean geometries as a mere logical exercise without any physical meaning.[1] And Wien, after he has mentioned the numerous investigations concerning the foundations of geometry in his lecture "On the transformation of the notion of space and time in physics", continues: "It is now remarkable, that contrary to these findings found in a pure speculative way, the possibility of a new notion of space and time has broken its way from experimental physics by induction. However, it has no direct connections to non-euclidean geometry.[2] I only want to mention Planck, according to whom this new conception of the notion of time "surpasses in boldness everything previously suggested in speculative natural phenomena and even in the philosophical theories of knowledge: non-euclidean geometry, which only comes seriously into consideration in pure mathematics, would be child's play in comparison."[3]
The intent of this lecture is to show that Lobachevskian geometry is seemingly the adequate instrument to handle the theory of relativity. The analogy between the two fields was noted by me, even before I was led to an intense study of Einstein's theory by Minkowski's Cologne lecture. In a lecture concerning the first period of development of non-euclidean geometry[4] I also mentioned the investigations concerning the admissible curvature measure of space or the length of the absolute unit distance of hyperbolic space. All lengths with which we have to deal, vanish against the unit distance and therefore the formulas of Lobachevskian geometry reduce themselves in regions of our empirical space to expressions of ordinary euclidean geometry. To make clear the relation of those geometries by an analogy from physics, I alluded to the relation of the mechanics of electrons to Newtonian mechanics; also the formulas of hyperbolic geometry asymptotically approach to the formulas of euclidean geometry. Later some additional but superficial analogies were noticed by me. The Lorentz contraction appeared to me as being an analogy to the deformation of lengths in well known interpretation of Lobachevskian geometry, where the straight lines were represented as half circles, and the line element it taken in the form . In general this line element cannot be moved without deformation. This led me to the assumption, whether the Lorentz contraction can be interpreted as the consequence of the geometrical anisotropy of space. In relativity theory the parallelogram of velocities is not valid; in Lobachevskian geometry there is no parallelogram at all. In relativity theory which banned the absolute from physics, there exists an absolute speed c; in Lobachevskian geometry there exists an absolute length R etc.. It didn't surprised me that there appeared analogies between the two fields also in the evolutionary history of these fields. In both cases we were struggling for the values of certain parameters, to which an infinite value was attributed in the older theories, and to which a finite value was attributed in recent theories. In the evolutionary history of non-euclidean geometry some apparent contractions were posed, and some thought to find contradictions in relativity theory as well.
All of this led me to transform Einstein's formulas and to interpret them in a non-euclidean way. In the mean time Sommerfeld's paper was published, in which it was shown that for the composition of velocities in relativity theory the formulas of spherical trigonometry with imaginary sides do apply.[5] Now, hyperbolic geometry is the imaginary counter-image of the spherical geometry, as it was already known to Lobachevsky and Bolyai. Then I was sure that an interesting field of application offers itself for the hyperbolic geometry. My first relevant papers in the Physikalische Zeitschrift were soon followed by two additional papers.[6] In those papers, I gave the non-euclidean interpretation of finished formulas in relativity theory. Afterwards I took the reverse way.[7] I based my thoughts on the assumption that the phenomena take place in Lobachevskian space and arrived by some simple geometrical conclusions at the formulas of relativity theory. The result of my investigation can be expressed as follows, that by using non-euclidean geometry the formulas for relativity theory were not only essentially simplified, but they also admit of a geometric interpretation that is completely analogous to the interpretation of classical theory in euclidean geometry. And this analogy sometimes goes thus far, that literal expression of the theorems of classical theory can remain unchanged, one only has to replace the euclidean figures by the corresponding figure of Lobachevskian space by the parameter .
1. Definition and graphical illustration of velocities.
The speed of light plays in physics the role of an infinitely great velocity. It cannot be reached by an accumulation of velocities less than the speed of light; it also cannot be changed by addition or subtraction of a velocity less than the speed of light. Now, by a suitable definition we can simply make that the speed of light is represented by an infinite quantity. As unit length we take , i.e. the light-path in a second, and then put
| (1) |
To velocity v we relate the length U of measure unit u according to the relation
| (2) |
Following the English style of writing this denotes the inverse function of the hyperbolic tangent. Now we want to investigate whether this definition is not in sharp contrast to the ordinary illustration of velocities. The distances proportional to the relevant velocities are used in ordinary mechanics as representing the velocities of uniform motions. Formula (2) leads to the same result at the limits of our ordinary experience. Only at velocities nearly comparable to the velocity of light, a notable difference occurs that quickly leads to infinite distortion.
We have put
| (3) |
If we take v = 1 km/sec at first, then
If we neglect everything after the first term on the right-hand side, then we commit an error that not even exerts an influence upon the 10th decimal. So by our definition, a length of 1 km is representing a velocity of 1 km/sec.
If we take the velocity of 100 km/sec which is in any case an extremely high velocity in ordinary mechanics, then it is given
For v = c we have , thus U = ∞.

In graphical illustration these relations can be easily summarized. If we take u as abscissa and as ordinate, then (2) will be represented by curve K. The straight line P or the first term in the infinite row (3), corresponds to the ordinary definition . The straight line is the inflexion tangent of K in O; so it fits well to the curve in the very far surrounding of the coordinate origin.
It seems convenient to introduce a name for length U. In my cited Serbian paper I have called it pseudo velocity. The easiest way would be, if we simply denote U and u as (physical) velocity and denote v as reduced velocity. As long as they are small, they practically cannot be distinguished. The pseudo velocity of light is infinitely great. By this definition it seems natural to us, that the velocity of light constitutes the upper limit for velocities.[8]
2. Einstein's addition law of velocities.
Also in relativity theory the vector addition of velocities is valid. One only has to graphically illustrate the components as it was explained above, and to use Lobachevskian trigonometry for the calculation of the resultant.

and are two velocities, that enclose the angle α with each other. The lengths with measure units correspond to them according to the relations
| (4) |
Then lay off the line from point O into the direction of , and apply the line under the angle α. The resultant corresponds to the line . In the Lobachevskian triangle OAB the relation is given
| (5) |
If we denote herein
| (6) |
then we obtain
and after some transformations
Eventually, from this it follows
| (7) |
and that is Einstein's addition law of velocities. In non-euclidean vector notation we can write it in the form
| (8) |
is only valid at first approximation, because one can put only for small velocities. If and are small compared to the speed of light, then one can neglect the last term in the numerator and denominator of expression (7), and one gets the ordinary formula
| (9) |
If one defines parameter c of our Lobachevskian space as infinitely small, then it goes over into euclidean space, and formula (7) is exactly reduced to (9). If velocities and enclose the angle α = 0, i.e. they lie in the same direction, then according to (5)
| (10) |
The resulting reduced velocity v follows from the formula
or
| (11) |
Although in the arithmetical sense the resultant is smaller as the sum of the components, it will be represented as in ordinary mechanics by a length equal to the sum of the lengths representing the components. If we compose two equal velocities in the same direction, then the resultant will be represented by the length .
On substitution (1) that paved me the way to the non-euclidean interpretation of relativity theory, I want to remark that Minkowski once put[9]
| (12) |
i.e., the expression of the velocity relation as tangens hyperbolicus, but he didn't pay further attention to the middle term of this relation. Also Herglotz had spoken out the conviction, that non-euclidean geometry con be applied in a useful way for the composition of velocities.[10] Now, recently an interesting paper was published by Robb,[11] in which he arrived in an odd way at results previously published by me already. On page 9 he namely says: "If v be the absolute velocity of the particle with respect to the system, then the inverse hyperbolic tangent of v will be spoken of as the rapidity. Thus if w be the rapidity,
As w increases from 0 to ∞, v increases from 0 to 1. For small values of w, practically, velocity is equal to rapidity, but we shall see latter that, for large values, it is the rapidity and not the velocity which follows the additive law." Then on p. 29: "Thus instead of a Euclidean triangle of velocities, we get a Lobatschefskij triangle of rapidities. For small rapidities, however, we may identify rapidity and velocity, and the Lobatschefskij triangle may be treated as an Euclidian one. It is also seen that rapidities in the same straight line are additive."
The difference in the ways, by which one arrives at the same results, strengthen the confidence in it.
3. The addition of velocities is not commutative.
In Lobachevskian geometry no parallelograms exist; the resultant of two velocities cannot be represented by a diagonal of a parallelogram. As a consequence the components are noncommutative. Because of simplicity we take two velocities under an angle . From formula (5) we obtain
| (13) |
from which we can easily derive
or
| (14) |
In figure 3 we have

If we lay off the length in the direction OC perpendicular to OA and apply under a right angle the line , then we come to point D different from B. In the older mechanics those points coincide. Thus if we compose these velocities in reverse order, we obtain a resultant of same magnitude but different direction. The direction difference
| (15) |
can easily be represented as a function of the components.
If we introduce into the formula
| (16) |
the values taken from the Lobachevskian triangle OAB
then we obtain
| (17( |
By (1) and (6) this goes over into
| (18) |
We also want to express this in a different way. The direction difference of the resultant is equal to the defect of triangle OAB. The content of a Lobachevskian triangle is equal to its defect. According to the known formula[12] for the defect we can put
| (19) |
or
| (20) |
If we compose three to each other perpendicular velocities in space, then we arrive at six resultants of different direction.
In Lobachevskian geometry there are no similar figures. On the other hand, in relativity theory there is no kinematic similarity. If we multiply all components by a number k, then in the older theory the resultant will be k-times greater as well, however, not in relativity theory. We would have to draw either the plans of forces as well as all figures in absolute measure. However, as the unit length is too great, we can give in both cases only schematic, distorted images.
4. The Weierstrass coordinates.
As unit length we take 1 cm, that is the th part of the absolute unit distance of our Lobachevskian space. We want to measure the unit time so as to make the speed of light equal to one, i.e. in the resting medium light traverses the unit length (1 cm) in a unit time.[13] We denote l as the new time that emerges from the old time by multiplication with the speed of light c as measured in the resting medium. We don't want to think of the considered clock as adjusted in the usual way, but as a simple clockwork that indicates, how often a certain (always repeating) process under the same circumstances, has happened since a certain event indicating the beginning of time counting.[14] By that we always express the time indication of a certain clock by a single number l = ct.
An elementary event is defined by the value system x, y, z, l. I interpret the defining magnitude of that event or the variables x, y, z, l as homogeneous Weierstrass coordinates of a point in Lobachevskian three-dimensional space.
Let as first take the simple case that z = 0.

Through point M (Fig. 4) we lay two limiting arcs MT and MV normal to the coordinate axes. The lengths of these arcs and the hyperbolic cosine of the traveling ray OM are Weierstrass coordinates of point M. If we lay off from point M the perpendiculars MP and MQ upon the coordinate axes, then the Lobachevskian coordinates of M are
Those of Weierstrass are
or
| (21) |
From the quadrilateral OPMQ of three right angles we obtain
in addition we have
| (22) |
and thus the Weierstrass coordinates are expressed by the Lobachevskian ones.

In the general case we have Fig. 5. N, R, S are the foot points of the three perpendiculars ξ η, ζ of M upon the coordinate plane, then
are the Lobachevskian, and
| (23) |
are the Weierstrass coordinates of point M.
From the quadrilateral MNRT we have[15]
while we obtain from OPNT the equation
From these two relations we obtain the expression for x. From the quadrilateral MNPS we easily find the value for y. The limiting arcs MA, MB and MC are our x, y, and z. We find in addition
and eventually
| (24) |
This relation is valid between the Weierstrass coordinates of every single point. It is known which role this invariant plays in Minkowski's four-dimensional interpretation of relativity theory.
5. The Lorentz-Einstein transformation.
The Galilei-Newton transformation
| (25) |
represents the translation along the X-axis in euclidean space. The Lorentz-Einstein transformation
| (26) |
similarly can be interpreted as a translation along the X-axis in Lobachevskian space.

If we remain in the plane then we can say: The Lorentz-Einstein transformation defines a motion along the distance line with the X-axis as its center line.[16]
This distance line Y = b is the location of the points having a constant distance b from the X-axis. The length of its arc between two points M and is (Fig. 6).
| (27) |
The displacement by the distance s along that equidistant line is defined by the equations
| (28) |
For the passage from to we have
or
| (29) |
If u is the projection of the arc in the X-axis, then
| (30) |
thus
| (31) |
By multiplication of the first equations by we have
| (32) |
According to Fig. 2 we have in addition
or
that is
| (33) |
Until now we have applied Lobachevskian coordinates; if we want to pass over to Weierstrass coordinates, then we have to consider the transformation formulas (22). By their aid we can bring equations (32) and (33) into the form
| (34) |
If we substitute herein according to formula (6)
and l = ct, then the Lorentz-Einstein transformation in its ordinary form (26) is immediately given. However, we always want to use them in the form (34). Indeed, we can see that the space-time transformation caused by a uniform motion of velocity u, will be completely characterized by the translation of point M representing an elementary event. The inverse transformation is
| (35) |
| (36) |
The invariants of first kind are
| (37) |
because . These are the distance lines Y = b.[17]
The invariants of second kind are the perpendiculars to the X-axis
| (38) |
because it is
In Lobachevskian right angled coordinates the equation of that perpendicular is X = u.
In space we obtain the distance lines with the X-axis as their center line, by the intersection lines of two distance areas
The center areas are the coordinate areas XY and XZ.
The L - E transformation (34), to which also equations z' = z have to be added, can be interpreted as a translation along the intersection line of these two equidistant areas. The orbital curve of a point of a rigid body during a translation along the X-axis is the distance line to the X-axis. The transverse dimensions of the body remain unchanged during this displacement.
If we take the parameter c = ∞, then the Lobachevskian space goes over to the euclidean space; the limiting arcs x, y, z become straight lines; Weierstrass coordinates are transformed into ordinary Cartesian coordinates, those distance lines become parallels to the X-axis; the transformation (34) or (26) goes over into (25).
6. Transformation of the time parameter.
From two observers moving uniformly but at different velocities on parallel paths, each of them can claim with the same justification, that they are at rest in respect to each other. Expressed in terms of geometry, this means that we can transform any point of the plane into a state of rest by relating it to a new coordinate system. From the related point, let fall the perpendicular upon the X-axis and use this perpendicular as the new ordinate axis. If we take, for example, the perpendicular through M, then XY is the coordinate system S, in which observer M (as he thinks) is at rest. However, if we move the coordinate origin to O', i.e., if we take as the fundamental system , then and all points of the new ordinate axis will be transformed into the state of rest. However, also the time parameter is changed by that transformation.
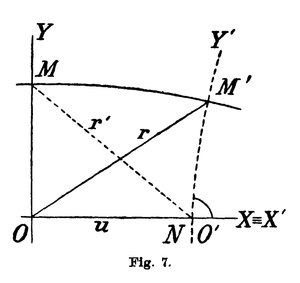
The unit time of the observer at a specific point shall be represented by the hyperbolic cosine of the Lobachevskian abscissa of that point. The unit time of the observer in O or in M is equal to "1" in the unprimed system, while the unit time of the observer in O'(M') becomes equal to , if we put OO' = u. For the observer resting in O it appears that the clock moving with velocity u stays behind in the ratio . When evaluating the duration of an event by means of the moving clock, the resting observer will find a smaller number. Thus there is the relation
| (39) |
or
However, in the primed system the unit time of the observer in is equal to "1", while the unit time of the observer in O is equal to . Both systems are completely and equally justified. Thus we cannot speak of a time duration per se. Consequently it is not allowed to speak about the simultaneity of two events in an absolute sense.

At first let us consider an example.[18] From a material point A at rest at the coordinate origin in a valid reference frame, a short light signal propagates in all directions at time l = 1. At time l > 1 the points that receive the signal are located on a sphere, of which we only want to consider the intersection circle with the XY-plane. On this circle two other material Points B and C at rest in S, may be located; therefore they simultaneously receive the signal, that is, by the same value l. Point D receives the signal a little later. However, if we lay through the point B and D a circle with center upon the abscissa axis, then is the system, in which the arriving of the light signals at points B and D was simultaneous. This system moves in respect to S with velocity . In the same way we could also define a reference frame in which the points A and B are simultaneous.
However, if point B is located at a limiting circle with the X-axis as its axis and adjacent to the ordinate axes at point A, then the perpendicular drawn at the bisecting point of line AB will be parallel to the X-axis. In this case there is no reference frame, in which the points A and B would be simultaneous.

Let us draw through O the limiting circles G and , with the positive or the negative side of the abscissa axis as their axis. Any point in the interior of those two limiting circles can be arranged in the reference frame as simultaneous with O. As, for example, point . If is the bisecting point of line , then the perpendicular raised in upon this line will intersect the X-axis in finite distance. If is located upon G, then the perpendicular raised in will be parallel to the X-axis. If we make this consideration for a point between those two limiting circles, the perpendicular raised in will diverge from the X-axis, because . The points on the limiting circles G, and in the hatched areas cannot be simultaneous with O in any reference frame.
In space we also would have two limiting spheres emerging from the rotation of those limiting circles around the X-axis.
According to relativity theory of optical phenomena in moving bodies, the speed of light in vacuum in the primed system is as high as in the unprimed. Additionally, light is propagating in all valid reference frames in all directions in an isotropic way. For the moving observer the infinitely thin light wave emerging from the instantaneous signal, propagates as a spherical wave, which is also the case for the stationary observer. The equation for the sphere or the circle will be transformed by (34) into the very same equation. In Weierstrass coordinates we can write the equations of the circle in the form or[19]
that is
| (40) |
if we put . In a point M(x,y) we lay the tangent at this circle, and from center O we let fall a limiting arc that is normal to the tangent; then is the length of this limiting arc. If we write (40) in the form
then because of (43) it goes over into
At this place I want to remind the words of Minkowski: "It cannot be a great problem for a mathematician, who is accustomed to considerations on multi-dimensional manifolds and also on the expressions of the so called non-euclidean geometry, to adapt the notion of time to the application of the Lorentz-transformation."[20] In connection with the things that were mentioned by Klein in his lecture "Geometrische Grundlagen der Lorentzgruppe", those primed words obtain a deeper meaning, and it would be very important to know, whether Minkowski has brought some of "his related inner considerations"[21] to paper?
7. Application of the transformation equations on some problems of optics.
The light vector of a plane light-wave propagating in vacuum, which is related to system S, shall be proportional to[22]
| (41) |
By means of transformation (35) this goes over into
or
| (42) |
We see, that F and can be represented in the same form, we only have to put
| (43) |
| (44) |
| (45) |
If we consider formulas (1) and (6), then we immediately obtain Einstein's formulas
| (46) |
| (47) |
| (48) |
To interpret this relation in a geometrical way, we want to resort to formulas (43)-(45), which will be altered by us so that only distances occur in them. It is a great advantage of Lobachevskian geometry, that we can express lengths and angles by magnitudes of the same kind, by either the introduction of the related parallel angle instead of length α, or the perpendicular a (of which α is the parallel angle) instead of any angle α.[23]
8. The principle of Doppler.
From equation (43) we can see the frequency that an observer moving along the X-axis with velocity v will find. The light ray encloses the angle with the X-axis (measured in System S). Considered as a parallel angle, this angle corresponds to the length , and therefore we have the relation
| (49) |
and (43) goes over into
| (50) |
from which we easily obtain
| (51) |

We take two equidistant lines (Fig. 10) with the X-axis as their common center line and with the parameters . The arcs of those two distance lines limited by the Y-axis and the perpendicular to the X-axis in point C, are
Thus it is
| (52) |
The ratio of the frequencies and can be represented in the general case as the ratio of the arcs of two distance lines between common perpendiculars.

Now, let us assume that light propagates in the direction of the X-axis. The parallel angle corresponds to the length , whose hyperbolic tangens is one. From (43) we obtain in this case
or
| (53) |
For those distance lines go over into the limiting circles with the common axes. Thus formula (53) agrees with Fig. 11. The ratio of the frequencies can also in this case be represented as the ratio of two limiting arcs between two common axes. From that formula it follows
and in this way we obtain Einstein's expression
| (54) |
From (53) it additionally follows
Higher powers of u can be neglected for small values; and if we replace the velocity u by the reduced velocity , then we obtain the expression of Doppler's principle of ordinary mechanics:
| (55) |
Note, that in the primed reference frame .
In euclidean geometry the distance lines and the limiting circles are reduced to parallels to the given straight line. Expression (55) can be easily illustrated by intersections of parallel transversals between the legs of an angle, because of relation .
9. Aberration
In the primed System the given light ray encloses the angle with the -axis. If we denote by the distance corresponding to the parallel angle , then (47) goes over into
or
| (56) |
Based on that aberration equation we have the following construction of the diverted light ray. A light ray T coming from an infinitely distant light source J, is striking the x-axis at point M under the acute angle φ. If we make , then . Then, we lay off the line toward the increasing abscissa, and from N we apply the Lobachevskian parallel to T. This parallel encloses the angle with the X-axis, because .
If , also , hence , and the angle goes over into its supplement . The diverted light ray is RJ.
The construction of the required parallel is executed in Fig. 13 as follows.[24] Put . From N we let fall the perpendicular NP upon T, then we construct the perpendicular NR upon NP in N, then we lay off the line MS equal to the absolute unit distance of our Lobachevskian space upon T, and from S we let fall the perpendicular SR upon NR. If we additionally make NU = PS, then NU will be parallel to T in the Lobachevskian sense, and this parallel encloses with the X-axis the angle .

Since point U lies always between S and R, it can easily be seen from the figure that in relativity theory is smaller than of ordinary mechanics.
In Einstein's formula for aberration, we denote the cosines on the left-hand side and in the numerator of the fraction by corresponding sines, then we square and obtain in this way after some transformations
| (57) |
During the motion of earth in its orbit relative to the fixed stars as reference frame we have . For such small velocities we can neglect , and then we approximately obtain
| (58) |
from which we easily find in agreement with ordinary theory
| (59) |
However, in this case we have to take instead of and instead of u.
Here, we also want to give another expression for aberration, that was geometrically interpreted by Plummer in two ways.[25] From (56) it follows
according to the relation existing between the perpendiculars and the corresponding parallel angle, this can be written in the form
| (60) |
10. The reflection of light at a moving mirror.
Let the coordinate plane be a perfect mirror. The light ray incident at the reflecting coordinate plane at point , is defined by the angle and the frequency ν. These magnitudes are related to the stationary system. The mirror is moving with velocity u in the direction of the positive abscissa axis of the stationary reference frame.
Instead of the parallel angle we want to consider the corresponding line . In the primed system the corresponding length according to (56) is
To the parallel angle of the reflected ray, we have the corresponding length
| (61) |
In the primed system the incident ray encloses the angle with the -axes; but after the reflection the angle is . According to the definition of the parallel angles for negative perpendiculars, the angle corresponds to the perpendicular when the supplementary angle corresponds to the perpendicular . If we consider the aberration equation (56), then we can see that for the observer resting in O, the length is increased by u. Thus we eventually come to the equation
| (62) |
from which we can see, that for the observer resting in O, the ray is reflected under the angle

| (63) |
From Fig. 14 the construction of the reflected ray according to formula (62) can be easily seen. For the construction it is advantageous to take the angle ψ supplementary to . By which ratio the angles ψ and φ are related, depends on the direction of the motion of the mirror relative to the light source. In the considered case , because ψ is related to the smaller perpendicular as parallel angle.
Now we can easily pass to Einstein's formulas. By (62) it is
or
| (64) |
Instead of the hyperbolic functions of the perpendiculars and , we introduce the spherical functions of the corresponding parallel angles, additionally we replace by and by this way we come to the formula of Einstein[26]
| (65) |
However, in the non-euclidean interpretation it will be completely replaced by the considerably simpler formulas (62) or (63).
By (51) and (62) we can construct, for the frequency of the reflected light rays, the formula
| (66) |
or
| (67) |
By introducing the parallel angle we obtain Einstein's expression
| (68) |
because the amplitudes were transformed in the same way as the frequencies. Fig. 15 is the geometrical image of formula (66).

The relations of the amplitudes and the frequencies of the incident and reflected light can be illustrated by the relation of the arc of two distance lines between common perpendiculars. The parameter of these distance lines are . We can easily see that we obtain by mirroring on . In the same way the angle can be defined by mirroring the incident ray on the aberrated ray.
For a normally incident light ray we have , also , the formula (66) goes over to
| (69) |
The relation of the frequencies and the amplitudes can in this case be illustrated as the relation of two coaxial limiting arcs. The corresponding figure would be the same as in Fig. 11, we only have to take .
The formula (51) for Doppler's principle and the aberration equation (56) have the same structure as the formula (66) for the frequency, the amplitude, and the formula (62) for the reflection angle of light reflected by a moving mirror. From this it follows, that the same light ray appears to be of the same constitution to an observer moving with the doubled velocity 2u, as it would appear to a stationary observer after the reflection by a mirror moving with velocity v. In both cases the motion must have the same direction.
Therefore we can obtain the laws for the reflection of light upon a moving mirror, by replacing u by 2u in formulas (34). However, as the image is located at the object's opposite side of the plane , we have to take instead of , i.e., we have to subject the light vector to the transformation
| (70) |
Now, it follows from (1)
and the preceding equations go over to
| (71) |
H. Bateman[27] has derived the laws of reflection on a moving mirror on the basis of the presupposition: the image of an object is caused by that space-time transformation (71).
The reflection angle at the moving mirror can be defined in the same way as at a stationary mirror, by means of construction according to the principle of Huyghens. I only mention the related statements by W. M. Hicks[28] and E. Kohl[29], performed by them with respect to the Michelson-Morley experiment. From our figure 14 we see, that or , when we denote by the perpendicular corresponding to angle ψ. From this it follows , or
| (72) |
This is the formula of Hicks. However, he assumes v to be positive when the ray moves towards the incident rays. In his formula (1) we have to take v as negative, to bring them into accordance to our definition.[30] In the same way we have to alter his figure.
- ↑ G. N. Lewis, A revision of the Fundamental Laws of Matter and Energy. Phil. mag., XVI, 1908, 709
- ↑ Separate print from Sitzungsberichte der Physikal. med. Gesellschaft zu Würzburg. Jahrgang 1909.
- ↑ Planck, Acht Vorlesungen über theoretische Physik, p. 117
- ↑ Published in Rad jugoslavenske akademije 169, 110-194, 1907
- ↑ A. Sommerfeld, On the Composition of Velocities in the Theory of Relativity. Physikalische Zeitschrift, 10, 828, 1909
- ↑ Physikalische Zeitschrift, 11, 93, 287, 586, 1910
- ↑ Sitzungsberichte der k. serbischen Akademie zu Belgrad, 88, 1911
- ↑ Norman Campbell, The Common Sense of Relativity, Phil. Mag., 1911, I, 508, says: "it is the fact that the second part of the Second Postulate proposes to represent the physically infinite velocity by a mathematically finite number which causes surprises. ... physical and mathematical infinity could by easily brought into agreement by a change of definition. This line of thought will be developed in a latter paper." Whether Campbell executed his plan, is not known to me. In Physik. Zeitschrift, XIII, 1912, 128, at the end of his respond to Wiechert, Campbell says, however, that such a ‚definition‘ would be very complicated.
- ↑ H. Minkowski, Zwei Abhandlungen über die Grundgleichungen der Elektrodynamik, 1910, p. 10, formula 2.
- ↑ G. Herglotz, Über den vom Standpunkt des Relativitätsprinzips aus als "starr" zu bezeichnenden Körper. Ann. d. Phys. 32, 404, 1910
- ↑ Alfred A. Robb, Optical geometry of motion; a new view of the theory of relativity, Cambridge 1911. His preface is dated 13. May 1911. My relevant investigations were published in Physikalische Zeitschrift of February 1st and April 1st 1910. Also my mentioned Serbian treatise was completed by the end of the year 1910.
- ↑ H. Liebmann, Nichteuklidische Geometrie, p. 149,
- ↑ A. Brill, Vorlesungen zur Einführung in die Mechanik, 204
- ↑ v. Mangoldt, Längen- und Zeitmessung in der Relativitätstheorie. Phys. Zeitschr. 11, 737, 1910
- ↑ F. Engel, Nikolaj Iwanowitsch Lobatschefskij. Zwei geometrische Abhandlungen, 1898, p. 347
- ↑ On the transformations of the Lobachevskian plane see my relevant papers in Rad jugoslavenske akademije 165, 50-80, 236-244, 1906, or the short excerpt therefrom in Jahresber. d. Deutsch. Mathematiker-Ver. 17, 80-83, 1908.
- ↑ H. Liebmann, Nichteuklidische Geometrie, 172
- ↑ M. Laue, Das Relativitätsprinzip, 1911, 35. M. Planck, Acht Vorlesungen über theoretische Physik, 1910, 118.
- ↑ H. Liebmann, Nichteuklidische Geometrie, 1905, 172
- ↑ H. Minkowski, Zwei Abhandlungen über die Grundgleichungen der Elektrodynamik, 1910, 19.
- ↑ Jahresbericht der Deutschen Mathematiker-Vereinigung, XIX, 1910, 299.
- ↑ A. Einstein, Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. Jahrb. d. Radioaktivität und Elektronik, 4, 1907, 424
- ↑ More about that in F. Engel, Nikolaj Iwanowitsch Lobatschefskij. Zwei geometrische Abhandlungen, 1898, 244
- ↑ Lobatschefskij-Engel. Zwei geometrische Abhandlungen, 256
- ↑ H. C. Plummer, On the Theory of Aberration and the Principle of Relativity. Monthly Notices of the Royal Astronomical Society, XX, 1910, 259
- ↑ Annalen der Physik, 17, 1905, 915
- ↑ H. Bateman, The reflexion of light at an ideal plane mirror moving with a uniform velocity of translation. Phil. Mag. 18, 892, 1909
- ↑ Phil. Mag. 3, 1902, 15
- ↑ Ann. d. Phys. 28, 1909, 262
- ↑ See also Laue, Das Relativitätsprinzip, 93
![]()
![]() This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
| Original: |
This work is in the public domain in the United States because it was published before January 1, 1929. The longest-living author of this work died in 1942, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 81 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
Public domainPublic domainfalsefalse |
|---|---|
| Translation: |
This work is released under the Creative Commons Attribution-ShareAlike 3.0 Unported license, which allows free use, distribution, and creation of derivatives, so long as the license is unchanged and clearly noted, and the original author is attributed.
Public domainPublic domainfalsefalse |









































































































































































































