On the Relative Motion of the Earth and the Luminiferous Ether
The discovery of the aberration of light was soon followed by an explanation according to the emission theory. The effect was attributed to a simple composition of the velocity of light with the velocity of the earth in its orbit. The difficulties in this apparently sufficient explanation were overlooked until after an explanation on the undulatory theory of light was proposed. This new explanation was at first almost as simple as the former. But it failed to account for the fact proved by experiment that the aberration was unchanged when observations were made with a telescope filled with water. For if the tangent of the angle of aberration is the ratio of the velocity of the earth to the velocity of light, then, since the latter velocity in water is three-fourths its velocity in a vacuum, the aberration observed with a water telescope should be four-thirds of its true value.[1]
On the undulatory theory, according to Fresnel, first, the ether is supposed to be at rest except in the interior of transparent media, in which secondly, it is supposed to move with a velocity less than the velocity of the medium in the ratio , where n is the index of refraction. These two hypotheses give a complete and satisfactory explanation of aberration. The second hypothesis, notwithstanding its seeming improbability, must be considered as fully proved, first, by the celebrated experiment of Fizeau,[2] and secondly, by the ample confirmation of our own work.[3] The experimental trial of the first hypothesis forms the subject of the present paper.
If the earth were a transparent body, it might perhaps be conceded, in view of the experiments just cited, that the inter-molecular ether was at rest in space, notwithstanding the motion of the earth in its orbit; but we have no right to extend the conclusion from these experiments to opaque bodies. But there can hardly be question that the ether can and does pass through metals. Lorentz cites the illustration of a metallic barometer tube. When the tube is inclined the ether in the space above the mercury is certainly forced out, for it is imcompressible.[4] But again we have no right to assume that it makes its escape with perfect freedom, and if there be any resistance, however slight, we certainly could not assume an opaque body such as the whole earth to offer free passage through its entire mass. But as Lorentz aptly remarks: "quoi qu’il en soit, on fera bien, à mon avis, de ne pas se laisser guider, dans une question aussi importante, par des considérations sur le degré de probabilité ou de simplicité de l’une ou de l’autre hypothèse, mais de s’addresser a l’expérience pour apprendre à connaitre l’état, de repos ou de mouvement, dans lequel se trouve l’ether à la surface terrestre."[5]
In April, 1881, a method was proposed and carried out for testing the question experimentally.[6]
In deducing the formula for the quantity to be measured, the effect of the motion of the earth through the ether on the path of the ray at right angles to this motion was overlooked.[7] The discussion of this oversight and of the entire experiment forms the subject of a very searching analysis by H. A. Lorentz,[8] who finds that this effect can by no means be disregarded. In consequence, the quantity to be measured had in fact but one-half the value supposed, and as it was already barely beyond the limits of errors of experiment, the conclusion drawn from the result of the experiment might well be questioned; since, however, the main portion of the theory remains unquestioned, it was decided to repeat the experiment with such modifications as would insure a theoretical result much too large to be masked by experimental errors. The theory of the method may be briefly stated as follows:
Let sa, fig. 1, be a ray of light which is partly reflected in ab, and partly transmitted in ac, being returned by the mirrors b and c, along ba and ca. ba is partly transmitted along ad,

and ca is partly reflected along ad. If then the paths ab and ac are equal, the two rays interfere along ad. Suppose now, the ether being at rest, that the whole apparatus moves in the direction sc, with the velocity of the earth in its orbit, the directions and distances traversed by the rays will be altered thus:— The ray sa is reflected along ab, fig. 2; the angle bab, being equal to the aberration =a, is returned along ba/, (aba/ =2a), and goes to the focus of the telescope, whose direction is unaltered. The transmitted ray goes along ac, is returned along ca/, and is reflected at a/, making ca/e equal 90—a, and therefore still coinciding with the first ray. It may be remarked that the rays ba/ and ca/, do not now meet exactly in the same point a/, though the difference is of the second order; this does not affect the validity of the reasoning. Let it now be required to find the difference in the two paths aba/, and aca/.
Let V= velocity of light.
- v= velocity of the earth in its orbit,
- D=distance ab or ac, fig. 1.
- T=time light occupies to pass from a to c.
- T =time light occupies to return from c to a/, (fig. 2.)
Then , . The whole time of going and coming is , and the distance traveled in this time is , neglecting terms of the fourth order. The length of the other path is evidently or to the same degree of accuracy, . The difference is therefore . If now the whole apparatus be turned through 90°, the difference will be in the opposite direction, hence the displacement of the interference fringes should be . Considering only the velocity of the earth in its orbit, this would be . If, as was the case in the first experiment, waves of yellow light, the displacement to be expected would be 0.04 of the distance between the interference fringes.
In the first experiment one of the principal difficulties encountered was that of revolving the apparatus without producing distortion; and another was its extreme sensitiveness to vibration. This was so great that it was impossible to see the interference fringes except at brief intervals when working in the city, even at two o'clock in the morning. Finally, as before remarked, the quantity to be observed, namely, a displacement of something less than a twentieth of the distance between the interference fringes may have been too small to be detected when masked by experimental errors.
The first named difficulties were entirely overcome by mounting the apparatus on a massive stone floating on mercury; and the second by increasing, by repeated reflection, the path of the light to about ten times its former value.
The apparatus is represented in perspective in fig. 3, in plan in fig. 4, and in vertical section in fig. 6. The stone a (fig. 5) is about 1.5 meter square and 0.3 meter thick. It rests on an annular wooden float bb, 1.5 meter outside diameter, 0.7 meter inside diameter, and 0.25 meter thick. The float rests on mercury contained in the cast-iron trough cc, 1.6 centimeter thick, and of such dimensions as to leave a clearance of about one centimeter around the float. A pin d, guided by arms gggg, fits into a socket e attached to the float. The pin may be pushed into the socket or be withdrawn, by a lever pivoted at f. This pin keeps the float concentric with the trough, but does not bear any part of the weight of the stone. The annular iron trough rests on a bed of cement on a low brick pier built in the form of a hollow octagon.
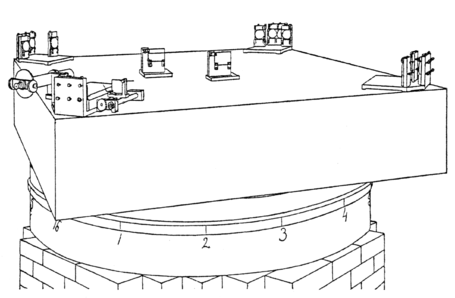
At each corner of the stone were placed four mirrors dd ee fig. 1. Near the center of the stone was a plane-parallel glass b. These were so disposed that light from an argand burner a, passing through a lens, fell on b so as to be in part reflected to d,; the two pencils followed the paths indicated in the figure, bdedbf and bd/e/d/bf respectively, and were observed by the telescope f. Both f and a revolved with the stone. The mirrors were of speculum metal carefully worked to optically plane surfaces five centimeters in diameter, and the glasses b and e were plane-parallel and of the same thickness. 1.25 centimeter; their surfaces measured 5.0 by 7.5 centimeters. The second of these was placed in the path of one of the pencils to compensate for the passage of the other through the same thickness of glass. The whole of the optical portion of the apparatus was kept covered with a wooden cover to prevent air currents and rapid changes of temperature.
The adjustment was effected as follows: The mirrors having been adjusted by screws in the castings which held the

mirrors, against which they were pressed by springs, till light from both pencils could be seen in the telescope, the lengths of the two paths were measured by a light wooden rod reaching diagonally from mirror to mirror, the distance being read from a small steel scale to tenths of millimeters. The difference in the lengths of the two paths was then annulled by moving the mirror e/. This mirror had three adjustments; it had an adjustment in altitude and one in azimuth, like all the other mirrors, but finer; it also had an adjustment in the direction of the incident ray, sliding forward or backward, but keeping very accurately parallel to its former plane. The three adjustments of this mirror could be made with the wooden cover in position.

The paths being now approximately equal, the two images of the source of light or of some well-defined object placed in front of the condensing lens, were made to coincide, the telescope was now adjusted for distinct vision of the expected interference bands, and sodium light was substituted for white light, when the interference bands appeared. These were now made as clear as possible by adjusting the mirror e/, then white light was restored, the screw altering the length of path was very slowly moved (one turn of a screw of one hundred threads to the inch altering the path nearly 1000 wavelengths) till the colored interference fringes reappeared in white light. These were now given a convenient width and position, and the apparatus was ready for observation.
The observations were conducted as follows: Around the cast-iron trough were sixteen equidistant marks. The apparatus was revolved very slowly (one turn in six minutes) and after a few minutes the cross wire of the micrometer was set on the clearest of the interference fringes at the instant of passing one of the marks. The motion was so slow that this could be done readily and accurately. The reading of the screw-head on the micrometer was noted, and a very slight and gradual impulse was given to keep up the motion of the stone; on passing the second mark, the same process was repeated, and this was continued till the apparatus had completed six revolutions. It was found that by keeping the apparatus in slow uniform motion, the results were much more uniform and consistent than when the stone was brought to rest for every observation; for the effects of strains could be noted for at least half a minute after the stone came to rest, and during this time effects of change of temperature came into action.
The following tables give the means of the six readings ; the first, for observations made near noon, the second, those near six o'clock in the evening. The readings are divisions of the screw-heads. The width of the fringes varied from 40 to 60 divisions, the mean value being near 50, so that one division means 0.02 wave-length. The rotation in the observations at noon was contrary to, and in the evening observations, with, that of the hands of a watch.
| Noon Observations. | |||||||||||||||||
| 16. | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. | 13. | 14. | 15. | 16. | |
| July 8 | 44.7 | 44.0 | 43.5 | 39.7 | 35.2 | 34.7 | 34.3 | 32.5 | 28.2 | 26.2 | 23.8 | 23.2 | 20.3 | 18.7 | 17.5 | 16.8 | 13.7 |
| July 9 | 57.4 | 57.3 | 58.2 | 59.2 | 58.7 | 60.2 | 60.8 | 62.0 | 61.5 | 63.3 | 65.8 | 67.3 | 69.7 | 70.7 | 73.0 | 70.2 | 72.2 |
| July 11 | 27.3 | 23.5 | 22.0 | 19.3 | 19.2 | 19.3 | 18.7 | 18.8 | 16.2 | 14.3 | 13.3 | 12.8 | 13.3 | 12.3 | 10.2 | 7.3 | 6.5 |
| Mean | 43.1 | 41.6 | 41.2 | 39.4 | 37.7 | 38.1 | 37.9 | 37.8 | 35.3 | 34.6 | 34.3 | 34.4 | 34.4 | 33.9 | 33.6 | 31.4 | 30.8 |
| Mean in w. l. | .862 | .832 | .824 | .788 | .754 | .762 | .758 | .756 | .706 | .692 | .686 | .688 | .688 | .678 | .672 | .628 | .616 |
| .706 | .692 | .686 | .688 | .688 | .678 | .672 | .628 | .616 | |||||||||
| Final mean | .784 | .762 | .755 | .738 | .721 | .720 | .715 | .692 | .661 | ||||||||
| P. M. Observations. | |||||||||||||||||
| July 8 | 61.2 | 63.3 | 63.3 | 68.2 | 67.7 | 69.3 | 70.3 | 69.8 | 69.0 | 71.3 | 71.3 | 70.5 | 71.2 | 71.2 | 70.5 | 72.5 | 75.7 |
| July 9 | 26.0 | 26.0 | 28.2 | 29.2 | 31.5 | 32.0 | 31.3 | 31.7 | 33.0 | 35.8 | 36.5 | 37.3 | 38.8 | 41.0 | 42.7 | 43.7 | 44.0 |
| July 12 | 66.8 | 66.5 | 66.0 | 64.3 | 62.2 | 61.0 | 61.3 | 59.7 | 58.2 | 55.7 | 53.7 | 54.7 | 55.0 | 58.2 | 58.5 | 57.0 | 56.0 |
| Mean | 51.3 | 51.9 | 52.5 | 53.9 | 53.8 | 54.1 | 54.3 | 53.7 | 53.4 | 54.3 | 53.8 | 54.2 | 55.0 | 56.8 | 57.2 | 57.7 | 58.6 |
| Mean in w. l. | 1.026 | 1.038 | 1.050 | 1.078 | 1.076 | 1.082 | 1.086 | 1.074 | 1.068 | 1.086 | 1.076 | 1.084 | 1.100 | 1.136 | 1.144 | 1.154 | 1.172 |
| 1.068 | 1.086 | 1.076 | 1.084 | 1.100 | 1.136 | 1.144 | 1.154 | 1.172 | |||||||||
| Final mean | 1.047 | 1.062 | 1.063 | 1.081 | 1.088 | 1.109 | 1.115 | 1.114 | 1.120 | ||||||||
The results of the observations are expressed graphically in fig. 6. The upper is the curve for the observations at noon, and the lower that for the evening observations. The dotted curves represent one-eighth of the theoretical displacements. It seems fair to conclude from the figure that if there is any displacement

due to the relative motion of the earth and the luminiferous ether, this cannot be much greater than 0.01 of the distance between the fringes.
Considering the motion of the earth in its orbit only, this displacement should be . The distance D was about eleven meters, or 2×107 wave-lengths of yellow light; hence the displacement to be expected was 0•4 fringe. The actual displacement was certainly less than the twentieth part of this, and probably less than the fortieth part. But since the displacement is proportional to the square of the velocity, the relative velocity of the earth and the ether is probably less than one sixth the earth's orbital velocity, and certainly less than one-fourth.
In what precedes, only the orbital motion of the earth is considered. If this is combined with the motion of the solar system, concerning which but little is known with certainty, the result would have to be modified; and it is just possible that the resultant velocity at the time of the observations was small though the chances are much against it. The experiment will therefore be repeated at intervals of three months, and thus all uncertainty will be avoided.
It appears, from all that precedes, reasonably certain that if there be any relative motion between the earth and the luminiferous ether, it must be small; quite small enough entirely to refute Fresnel's explanation of aberration. Stokes has given a theory of aberration which assumes the ether at the earth's surface to be at rest with regard to the latter, and only requires in addition that the relative velocity have a potential; but Lorentz shows that these conditions are incompatible. Lorentz then proposes a modification which combines some ideas of Stokes and Fresnel, and assumes the existence of a potential, together with Fresnel's coefficient. If now it were legitimate to conclude from the present work that the ether is at rest with regard to the earth's surface, according to Lorentz there could not be a velocity potential, and his own theory also fails.
Supplement.
It is obvious from what has gone before that it would be hopeless to attempt to solve the question of the motion of the solar system by observations of optical phenomena at the surface of the earth. But it is not impossible that at even moderate distances above the level of the sea, at the top of an isolated mountain peak, for instance, the relative motion might be perceptible in an apparatus like that used in these experiments. Perhaps if the experiment should ever be tried in these circumstances, the cover should be of glass, or should be removed.
It may be worth while to notice another method for multiplying the square of the aberration sufficiently to bring it within the range of observation, which has presented itself during the preparation of this paper. This is founded on the fact that reflection from surfaces in motion varies from the ordinary laws of reflection.
Let ab (fig. 1) be a plane wave falling on the mirror mn at an incidence of 45°. If the mirror is at rest, the wave front after reflection will be ac.
Now suppose the mirror to move in a direction which makes an angle a with its normal, with a velocity . Let V be the velocity of light in the ether supposed stationary, and let cd be the increase in the distance the light has to travel to reach d. In this time the mirror will have moved a distance . We have which put = r, and .
In order to find the new wave front, draw the arc fg with b as a center and ad as radius; the tangent to this arc from d will be the new wave front, and the normal to the tangent from b will be the new direction. This will differ from the direction ba by the angle which it is required to find. From the equality of the triangles adb and edb it follows that , ,
or neglecting terms of the order ,
Now let the light fall on a parallel mirror facing the first, we should then have and the total deviation would be where is the angle of aberration, if only the orbital motion of the earth is considered. The maximum displacement obtained by revolving the whole apparatus through 90° would be . With fifty such couples the displacement would be 0•2". But astronomical observations in circumstances far less favorable than those in which these may be taken have been made to hundredths of a second; so that this new method bids fair to be at least as sensitive as the former.
The arrangement of apparatus might be as in fig. 2; s in the focus of the lens a, is a slit; bb cc are two glass mirrors optically plane and so silvered as to allow say one-twentieth of the-light to pass through, and reflecting say ninety per cent. The intensity of the light falling on the observing telescope df 
If it were possible to measure with sufficient accuracy the velocity of light without returning the ray to its starting point, the problem of measuring the first power of the relative velocity of the earth with respect to the ether would be solved. This may not be as hopeless as might appear at first sight, since the difficulties are entirely mechanical and may possibly be surmounted in the course of time.
For example, suppose (fig. 3) m and m/, two mirrors revolving with equal velocity in opposite directions. It is evident that light from s will form a stationary image at s/ and similarly light from s/ will form a stationary image at s. If now the velocity of the mirrors be increased sufficiently, their phases still being exactly the same, both images will be deflected from s and s/, in inverse proportion to the velocities of light in the two directions; or, if the two deflections are made equal, and the difference of phase of the mirrors be simultaneously measured, this will evidently be proportional to the difference of velocity in the two directions. The only real difficulty lies in this measurement. The following is perhaps a possible solution : gg/ (fig. 4) are two gratings on which sunlight is concentrated. These are placed so that after falling on the revolving mirrors m and m/, the light forms images of the gratings at s and s/, two very sensitive selenium cells in circuit with a battery and a telephone. If everything be symmetrical, the sound in the telephone will be a maximum. If now one of the slits s be displaced through half the distance between the image of the grating bars, there will be silence. Suppose now that the two deflections having been made exactly equal, the slit is adjusted for silence. Then if the experiment be repeated when the earth's rotation has turned the whole apparatus through 180°, and the deflections are again made equal, there will no longer be silence, and the angular distance through which s must be moved to restore silence will measure the required difference in phase.
There remain three other methods, all astronomical, for attacking the problem of the motion of the solar system through space.
1. The telescopic observation of the proper motions of the stars. This has given us a highly probably determination of the direction of this motion, but only a guess as to its amount.
2. The spectroscopic observation of the motion of stars in the line of sight. This could furnish data for the relative motions only, though it seems likely that by the immense improvements in the photography of stellar spectra, the information thus obtained will be far more accurate than any other.
3. Finally there remains the determination of the velocity of light by observations of the eclipses of Jupiter's satellites. If the improved photometric methods practiced at the Harvard observatory make it possible to observe these with sufficient accuracy, the difference in the results found for the velocity of light when Jupiter is nearest to and farthest from the line of motion will give, not merely the motion of the solar system with reference to the stars, but with reference to the luminiferous ether itself.
Notes
[edit]- ↑ It may be noticed that most writers admit the sufficiency of the explanation according to the emission theory of light; while in fact the difficulty is even greater than according to the undulatory theory. For on the emission theory the velocity of light must be greater in the water telescope, and therefore the angle of aberration should be less; hence, in order to reduce it to its true value, we must make the absurd hypothesis that the motion of the water in the telescope carries the ray of light in the opposite direction!
- ↑ Comptes Rendus, xxxiii, 349, 1851; Pogg. Ann. Ergänzungsband, iii. 457, 1853; Ann. Chim. Phys., III, lvii, 385, 1859.
- ↑ Influence of Motion of the Medium on the Velocity of Light. This Journal, III, xxxi, 377, 1886.
- ↑ It may be objected that it may escape by the space between the mercury and the walls; but this could be prevented by amalgamating the walls.
- ↑ Archives Néerlandaises, xxi, 2me livr.
- ↑ The Relative Motion of the Earth and the Luminiferous Ether, by Albert A. Michelson, this Jour., III xxii, 120.
- ↑ It may be mentioned here that the error was pointed out-to the author of the former paper by M. A. Potier, of Paris, in the winter of 1881.
- ↑ De l'Influence du Mouvement de la Terre sur les Phen. Lum. Archives Néerlandaises, xxi, 2me livr., 1886.
![]()
This work is in the public domain in the United States because it was published before January 1, 1929.
The longest-living author of this work died in 1931, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 92 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
![]()
Public domainPublic domainfalsefalse

























