A Dictionary of Music and Musicians/Modes, The Ecclesiastical

MODES, THE ECCLESIASTICAL. One of the most prominent features in Greek music was the division of the Diatonic Scale into certain regions called Modes. The musicians of the Middle Ages, who confessedly derived their idea of the scale from Hellenic sources, adopted an analogous peculiarity into their own system, in which it at once took root, though its development was very gradual. At first, four forms only were recognised, in the newer method—the Authentic Modes of Saint Ambrose. To these—if tradition may be trusted—Saint Gregory added four Plagal scales. Later theorists taught the existence of fourteen varieties; twelve of which remained, for many centuries, in constant use, distinguished by the names of their Greek prototypes, though not really identical with them; while two were rejected, as impure, and practically useless.

Into the laborious process by which these scales were evolved from the complicated mysteries of the Greek Canon we need not enter. To us, their construction is simple enough, when regarded from our own point of view. We have only to imagine a series of the natural notes of the modern Diatonic Scale, extending, upwards, from A, the first space in the bass, to C, the third space in the treble. By dividing this grand scale into sections, each consisting of eight notes, and each beginning with a different sound, we shall obtain the entire set of fourteen Modes, in the most complete form possible.

The Modes are separated into two classes: Authentic, (from αὐθεντέω, to govern) and Plagal, (from πλάγιος, oblique). The compass of the former extends from the Final (equivalent to the Tonic, or Key-note, of modern theory,) to the Octave above. That of the latter, from the Fourth below the Final, to the Fifth above it. Consequently, the Final is the lowest note of the Authentic Modes; and (very nearly) the middle note of Plagal ones. Every Plagal Mode is derived from an Authentic original, from which it is distinguished, in name, by the prefix, Hypo-: the same Final being common to both forms; and the compass of the derived Mode lying a Fourth below that of the original scale. In the following table, the Final of each Mode is indicated by the letter F; and, the position of the semitones, by a slur.

AUTHENTIC MODES.	PLAGAL MODES

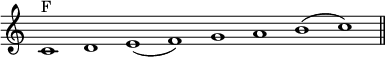Each of these Modes is divisible into two members, a Pentachord, and a Tetrachord. The notes which compose the Pentachord are contained within the compass of a Perfect fifth, (Diapente): those of the Tetrachord, within that of a Perfect Fourth, (Diatessaron). In the Authentic Modes, the Fifth is placed below the Fourth: in the Plagal, the Fourth lies below the Fifth. The former is called the 'Harmonic,' and the latter, the 'Arithmetical Division.'^[1] In both cases, the highest note of the lower member corresponds with the lowest of the upper: thus—

HARMONIC DIVISION.

ARITHMETICAL DIVISION.

It will be seen, that, in the Locrian and Hypolocrian Modes, this division is impossible; since in both cases it would substitute, for the perfect intervals, a Diminished Fifth, (Quinta falsa), and an Augmented Fourth, (Tritonus). On this account these Modes are condemned as impure. Some authorities expunge even their names and numbers from the catalogue; calling the Ionian the Eleventh, and the Hypoionian the Twelfth Mode. Others—among whom are the editors of the Ratisbon, Mechlin, and Rheims-Cambrai Office-Books—retain the names and numbers, but, none the less, reject the scales themselves. The true number of the Modes has, indeed, been many times disputed: once, so hotly, that the question was referred to the decision of Charlemagne; who at first said that eight seemed to be sufficient, but afterwards allowed the use of twelve. More than one later theorist, while nominally recognising the existence of eight forms only, has described Modes IX,X,XI, XII, XIII, and XIV,as metamorphosed renderings of I, II, III, IV, V, and VI, respectively. Hence, we constantly find, in the Mechlin Office-Books, such expressions as 'I Modus, antiquitus IX,' or 'X Modus; alii reduxerunt ad II': a distinction sufficiently puzzling to the tyro, from the confusion it creates with regard, both to the nature and the true Final of the disputed scale.

Besides its Final, every Mode is distinguished by three other highly characteristic notes—its Dominant, Mediant, and Participant—the relative importance of which is shewn by the order in which we have mentioned them.

The Dominant of the Authentic Mode lies a Fifth above the Final; unless that note should happen to be B, in which case C is substituted for it. That of the Plagal Modes lies a Third below the Authentic Dominant; unless that third note should happen to be B, in which case C is substituted, as before. In both cases, B is prevented from serving as a Dominant by its dissonant relation with F. The only exception to the general rule is found in the Locrian Mode, the Dominant of which is G, the sixth from the Final. The Hypolocrian Mode follows the strict law. In the Gregorian Psalm Tones, the Dominant is the note upon which the recitation of the greater part of every verse takes place.

The Mediant—so called from its position between the Final and Dominant—is always the third of the scale, in the Authentic Modes; unless that note should happen to be B, in which case C is substituted for it. In the Plagal Modes, its position is less uniform.

The Participant is an auxiliary note, generally in the immediate neighbourhood of the Mediant, in Authentic Modes; and, in the Plagal forms, coincident with the Dominant of the corresponding Authentic scale. Some Modes have a second Participant; and one has a second Mediant, which, however, is not very frequently used.

Each Mode is also influenced by certain notes, called its Modulations, or Cadences, which are of two kinds. The Regular Modulations are, the Final, Dominant, Mediant, and Participant, already mentioned. To these are added two or more subsidiary notes, called Conceded Modulations, (Modulationes concessæ,) among which we often find the inverted Seventh—i.e. the Seventh, taken an Octave lower than its true pitch, and, consequently, one degree below the natural compass of the scale.

Upon one or other of these Modulations, either Regular, or Conceded, every phrase of every melody must begin, and end: subject only to two farther restrictions—(1) The first phrase must begin on one of a somewhat less ample series of notes, called the Absolute Initials; (2) The last phrase can only end on the Final of the Mode.

The following Table shews the Compass, Final. Dominant, Mediant, Participant, Regular and Conceded Modulations, and Absolute Initials, of every Mode in the series, including the Locrian, and Hypolocrian, which, in spite of their manifest imperfection, have sometimes been used in sæcular music.

					Modulations.
			Regular.				Conceded.
Numbers.	Names of the Modes.	Range.	Fin.	Dom.	Med.	Part.	Mod. Con.	Absolute Initials.
I.	Dorian.	D–D	D	A	F	G	C1. E	C1. D. F. G. A
II.2	Hypodorian.	A–A	D	F	E	A. A3	C.G	A. C. D. E4. F
III.	Phrygian.	E–E	E	C	G	A. B	D1. F	E. F. G4. C
IV.2	Hypophrygian.	B–B	E	A	G	C. F	D. B3	C. D. E. F. G4. A4
V.	Lydian.	F–F	F	C	A	G	B. D. E	F. A. C
VI.2	Hypolydian.	C–C	F	A	D	C6	B1. G. B [♭]	C6. D4. F
VII.	Mixolydian.	G–G	G	D	C	A	B. E	G. A4. B. C. D.
VIII.2	Hypomixolydian.	D–D	G	C	F. A	D6	B. D3	C1. D. F. G. A. C
IX.	Æolian.	A–A	A	E	C	D	G1. B	G1. A. C. D. E
X.2	Hypoæolian.	E–E	A	C	B	E. E3	G. D	E. G. A. B4. C
XI.	Locrian.	B–B	B	G	D	E. F	A1. C	B. C4. D. G
XII.2	Hypolocrian.	F–F	B	E	D	G. C	A. F3	G. A. B. C. D4. E4
XIII (or XI).	Ionian.	C–C	C	G	E	D	F. A. B	C. D5. E. G
XIV (or XII.)2	Hypoionian.	G–G	C	E	A	G6	F1. D. F	G6. A. C. D5.

¹ The Inverted 7th.⁠² Plagal Modes.⁠³ The 5th above the Final.
⁴ Barely used in an Absolute Initial.
⁵ Used as an Absolute Initial chiefly in polyphonic music.
⁶ The lowest note of the Mode.

In vindication of the use of the Inverted Seventh, it is necessary to explain, that, under certain conditions, the normal compass of all the Modes may be slightly extended. Every Authentic Mode may, by license, descend one degree below its Final: the Phrygian Mode may descend two. Every Plagal Mode may ascend to the sixth degree above the Final: the Hypolydian, and Hypomixolydian Modes, may, in addition, descend to the fifth below it.

Melodies confined strictly within the natural range of the Mode are called Perfect; those which fall short of it, Imperfect; those which exceed it, Superfluous. A melody which combines the entire compass of a Plagal with that of an Authentic scale, is said to be in a Mixed Mode.

Both in Plain Chaunt and Polyphonic Music, the Modes are used, sometimes, at their true pitch; sometimes, transposed a Fourth higher, (or Fifth lower), by means of a B flat at the Signature. No accidentals are permitted, in Plain Chaunt, except an occasional B flat, introduced for the purpose of correcting a Tritonus, or a False Fifth—the use of both these intervals being strictly forbidden, whether in disjunct or conjunct movement. [See Plain Chaunt [App. p.719 "Plain Song".] The Canto fermo, in Polyphonic Music, is as strictly subject to the laws of the Mode as a Plain Chaunt melody—which, in fact, it generally is: but, in the Counterpoint, the use of certain sharps, flats, and naturals, is sometimes directly enjoined, in conformity with precepts which will be found fully described elsewhere. [See Musica Ficta.]

In order to ascertain the Mode in which a Plain Chaunt Melody is written, observe the last note, which will, of course, shew the required Final. Should the compass of the Melody lie between that Final and its Octave, the Mode will be Authentic. Should it lie between the fifth above and the Fourth below, it will be Plagal. Should it extend throughout the entire range, from the Fourth below the Final to the Octave above it, it will be Mixed. Should there be a B flat at the Signature, it will indicate that the Mode has been transposed; and the true Final will then lie a Fourth below the written one. For example, the Plain Chaunt Melody, 'Angelus autem Domini' (for which see the article, Antiphon), has no B flat at the Signature. Its last note is G, the Mixolydian Final. Its compass lies between the Fifth above that note, and the Second below it. It is, therefore, in the Eighth, or Hypomixolydian Mode; and, as its range falls two degrees short of the full downward range of the scale, it belongs to the class of Imperfect Melodies.

To ascertain the Mode of a polyphonic composition, examine the last note in the Bass. This will be the Final. Then, should the range of the Canto fermo—which will almost always be found in the Tenor—lie between the Final and its Octave, the Mode will be Authentic. Should it lie between the Fifth above and the Fourth below, it will be Plagal. Should there be a B flat at the Signature, it will shew that the Mode has been transposed; and the true Final will then lie a Fourth below the last bass note. Thus, Palestrina's Motet, 'Dies sanctificatus,' has no B flat at the Signature. The last note in the Bass is G. The compass of the Canto fermo, as exhibited in the Tenor, lies, almost entirely, between that note and its Octave. The Motet, therefore, is in the Seventh, or Mixolydian Mode. The same composer's Missa Æterna Christi munera' has a B flat at the Signature, and is, therefore, transposed. The last note in the Bass is F, the Fourth below which is C—the Ionian Final. The compass of the Canto fermo, in the Tenor, lies between the transposed Final, and its Octave. Consequently, the Mass is in the Thirteenth, or Ionian Mode, transposed.

According to strict law, it is as necessary for the Canto fermo to end on the Final of the Mode as the Bass: but, when the last Cadence is a very elaborate one, it frequently contents itself with just touching that note, and then glancing off to others, after the manner of what we should now call a coda. The neophyte will always, therefore, find the last Bass note his safest guide, in this particular. [See Polyphonic Music [App. p.719 "Polyphonia".]

In order to accommodate the range of 'unequal' voices, it constantly happens, that the Treble and Tenor, are made to sing in an Authentic Mode, while the Alto and Bass sing in a Plagal one; and vice versa. In these cases, the true character of the Mode is always decided by the compass of the Canto fermo.

[ W. S. R. ]

1. Vide Morley's Plaine & easie Introduction to Practical Musicke. (London 1597.)